数据结构与算法:栈
栈(stack)又名堆栈,它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
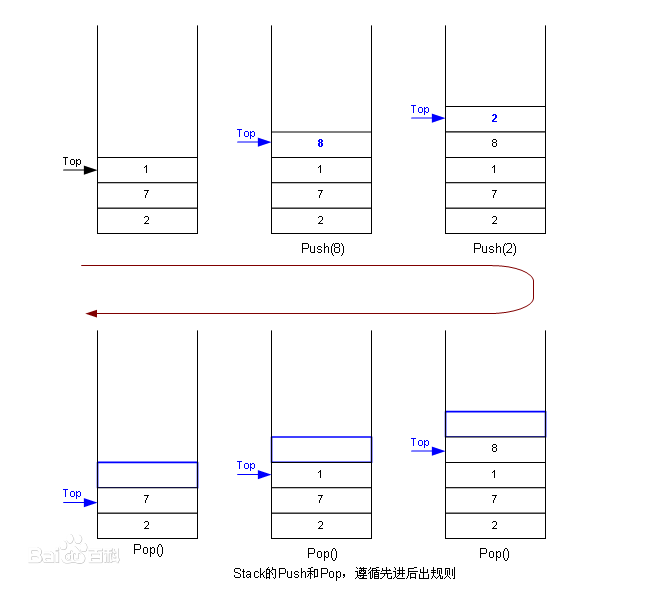
使用数组模拟栈
public class ArrayStackDemo { public static void main(String[] args) { //测试数组模拟栈 ArrayStack arrayStack = new ArrayStack(5); boolean loop = true; String key = ""; Scanner scanner = new Scanner(System.in); while (loop){ System.out.println("list:遍历栈内数据"); System.out.println("exit:退出程序"); System.out.println("push:向栈内推入数据"); System.out.println("pop:从栈内取出数据"); key = scanner.next(); switch (key){ case "list": arrayStack.list(); break; case "push": int value = scanner.nextInt(); arrayStack.push(value); break; case "pop": try { int result = arrayStack.pop(); System.out.printf("取出的数据为:%d\n", result); }catch (Exception e){ System.out.println(e.getMessage()); } break; case "exit": scanner.close(); loop = false; break; default: break; } } System.out.println("程序已退出!"); } } //数组模拟栈的类 class ArrayStack{ private int maxSize; //栈的最大容量 private int[] arrayStack; //数组模拟栈 private int top = -1; //模拟栈的顶端指针,指向栈的顶端,默认为-1,即栈空 public ArrayStack(int maxSize) { this.maxSize = maxSize; arrayStack = new int[maxSize]; } /** * 因为栈是从索引为0的底端开始压入数据的,所以 * 当顶端指针为maxSize-1时,栈为满 * 当顶端指针为-1时,栈为空 */ public boolean isFull(){ //判断是否为满 return top == maxSize-1; } public boolean isEmpty(){ //判断是否为空 return top == -1; } /** * 思路: * 1. 顶端指针top向后移一位 * 2. 将数据存放在指针指向的位置 * @param data */ public void push(int data){ //向栈内压入数据 if (isFull()){ System.out.println("栈满!"); return; } top++; arrayStack[top] = data; } /** * 思路: * 1. 将顶端指针top指向的位置的数据弹出 * 2. 将顶端指针top向前移一位 * @return */ public int pop(){ if (isEmpty()){ throw new RuntimeException("栈为空!"); } int result = arrayStack[top]; top--; return result; } public void list(){ //遍历数组模拟栈 if (isEmpty()){ System.out.println("栈为空!"); return; } for (int i=top; i>=0; i--){ System.out.printf("arrayStack[%d]=%d\n", i, arrayStack[i]); } } }
栈的应用——表达式求值
在我们日常中使用的表达式,如:(30+2)*5-16/4,称做中缀表达式。它对于我们来说是易理解的,但对于计算机来说却是非常复杂的,所以我们需要把表达式换做在计算器看来简单的易懂的后缀表达式(逆波兰表达式),如:30 2 + 5 * 16 4 / -。而栈就能帮我们把中缀表达式转换成后缀表达式。
中缀表达式转后缀的逻辑:
是以从左到右,按运算先后的顺序来转换的,运算符则放在运算数的后面,如 a+b-c 就是 a b + c -
以(30+2)*5-16/4为例,流程为
-
30+2 转换为 30 2 +
-
(30+2)*5 转换为 30 2 + 5 *
-
16/4 转换为 16 4 /
-
(30+2)*5-16/4 转换为 30 2 + 5 * 16 4 / -
代码实现
public class RPNCalculator { public static void main(String[] args) { String expression = "(30+2)*5-16/4"; //对应的后缀表达式为"30 2 + 5 * 16 4 / -" List<String> expressionList = splitToArrayList(expression); System.out.println(expressionList);//输出原先的中缀表达式 List<String> suffixExpression = toSuffixExpression(expressionList); System.out.println(suffixExpression);//输出转换后的后缀表达式 System.out.println(expression+"="+calculator(suffixExpression));//输出计算后的最终结果 } /** * 将中缀表达式转为后缀表达式 * 逻辑思路: * 遍历中缀表达式集合: * 1.如果是数字,直接存进后缀表达式集合中 * 2.如果是括号"()": * 1)如果是"(", 直接压入操作符栈中 * 2)如果是")", 则遍历操作符栈,查看操作符栈的顶端是否是"(", * 如果不是则把顶端弹出添加到后缀表达式集合中,是则直接把"("从栈弹出即可 * 3.如果是其他操作符: * 1)如果操作符栈为空,则直接压入栈中 * 2)如果不为空,则和栈顶操作符比较优先级,如果栈顶操作符优先级>=传入的操作符优先级, * 则先将栈顶操作符弹出并添加到后缀表达式集合中,再把传入操作符压入栈中 * 不是则直接压入栈中 * 遍历完中缀表达式集合后,再把操作符栈中剩余的操作符弹出并添加到后缀表达式集合中 * @param expression 中缀表达式集合 * @return */ public static List<String> toSuffixExpression(List<String> expression){ Stack<String> operator = new Stack<>();//操作符栈,用于储存操作符 List<String> suffixExpression = new ArrayList<>();//后缀表达式数组集合 for (String item : expression){//遍历中缀表达式中的每个数据 if (item.matches("^-?\\d+$")){//使用正则表达式判断该字符串是否是整数 suffixExpression.add(item);//如果是整数则直接加集合中 }else if (item.equals("(")){ operator.push(item);//如果是(,则压入操作符栈中 }else if (item.equals(")")){ while( !operator.peek().equals("(") ){//判断栈顶是否是"(" suffixExpression.add(operator.pop());//如果不是则弹出栈顶并添加到后缀表达式集合中 } operator.pop();//最后在把栈底的"("弹出 }else {//非括号的其他操作符 //栈为空 或 优先级>=栈顶的操作符 则将栈顶操作符弹出并添加到后缀表达式集合中 while (!operator.isEmpty() && priority(item) <= priority(operator.peek())){ suffixExpression.add(operator.pop()); } operator.push(item);//最后再把操作符压入栈中 } } while ( !operator.isEmpty() ){//把操作符栈中剩下的操作符弹出并添加到后缀表达式集合中 suffixExpression.add(operator.pop()); } return suffixExpression; } //计算方法 public static int calculator(List<String> suffixExpression){ Stack<Integer> numStack = new Stack<>();//用于储存表达式中每段计算的结果 int result = 0; for (String item : suffixExpression){//遍历后缀表达式集合 if (item.matches("^-?\\d+$")){//判断是否是整数 numStack.push(Integer.parseInt(item));//如果是则直接压入栈中 }else { //如果是操作符,则从栈中弹出俩个数字并计算结果 int num1 = numStack.pop(); int num2 = numStack.pop(); switch (item){ case "+": result = num1 + num2; break; case "-": result = num2 - num1; break; case "*": result = num1 * num2; break; case "/": result = num2 / num1; break; default: throw new RuntimeException("表达式含有未能识别的符号!"); } numStack.push(result);//再把计算后的结果压入栈中 } } //最后栈中剩余的唯一数据就是表达式最后的计算结果 return numStack.pop(); } //将表达式的字符串分割成数组集合 public static List<String> splitToArrayList(String expression){ List<String> expressionList = new ArrayList<>(); int index = 0;//字符串下标,用于字符串内的字符的锁定 char c = ' '; String s = "";//用于拼接数字 while (index < expression.length()){//判断下标是否已超出字符串长度 c = expression.charAt(index);//根据下标从字符串取出相应的字符 if (c > 47 && c < 58){//根据ascii码判断字符是否是数字 s += c;//把数字添加到拼接字符串 while (index<expression.length()-1 && expression.charAt(index+1)>47 && expression.charAt(index+1)<58){//判断是否是多位数 //如果是多位数,将下个下标的字符也添加进拼接字符串 s += expression.charAt(index+1); index++; } expressionList.add(s); s = "";//将拼接字符串清空 }else {//如果为其他字符则直接添加进集合中 expressionList.add(c+""); } index ++; } return expressionList; } //返回各个操作符的优先级 public static int priority(String s){ switch (s){ case "+": case "-": return 1; case "*": case "/": return 2; case "(": case ")": return 0; default: throw new RuntimeException("表达式含有未能识别的符号!"); } } }
翻译 朗读 复制 正在查询,请稍候…… 重试 朗读 复制 复制 朗读 复制 via 谷歌翻译(国内) 译



