一致性哈希

在 1997 年，MIT 的计算机科学实验室研究员 David Karger, Eric Lehman, Tom Leighton, Matthew Levine, Daniel Lewin, Rina Panigrahy 等发表了论文《Consistent hashing and random trees: distributed caching protocols for relieving hot spots on the World Wide Web》，提出了一致性哈希（Consistent Hashing）的概念，其设计目标是为了解决大型网络中的热点问题（Hot Spots）。

在实际应用中，有很多需要将一个 Item 分布到多个 Bucket 中的场景：

• 将数据加载到内存中（Data --> Memory）
• 将文件写入到磁盘中（File --> Disk）
• 将任务分配到处理器（Task --> Processor）
• 将页面加载到缓存中（Page --> Cache）

在这些场景中，我们的设计目标就是要将 Item 均匀地分布（Even Distribution）到不同的 Bucket 中，也就是负载均衡（Load Balancing）。

对于负载均衡中的负载，我们实际上会面对两种情况：

• 持续性的负载（Permanent Loads）
• 临时性的负载（Temporary Loads）

对于持续性的负载可以通过提高服务器的能力或者通过添加固定数量的机器来分担压力。而临时性的负载则是最难处理的，这需要系统的设计能够抵御突发的请求高峰。

对于处理临时性的负载，通常我们会考虑使用缓存代理（Proxy Caching）技术，它使得对 Home 主机的访问模式由原先的每次浏览均访问一次转换到每个页面仅访问一次。

在使用 Cache 机制时，会遇到多种情况：

• 如果某一个 Cache 持有了大量的 Items，则该 Cache 将被大量的客户请求所淹没。所以 Cache 应该持有较少的 Items。
• 如果某一个 Item 会被大量的 Cache 所持有，则 Cache 对 Home 的请求将会成为压力的来源。所以 Item 应该被放入到少量的 Cache 中。
• 如果请求方不知道正确的 Cache 位置，则需要 Server 端重定向，则重定向 Server 将成为瓶颈。所以请求方必须知道 Cache 的正确位置。

通常，使用 Hashing 技术可以提供简单有效的负载均衡。Hashing 使得查找存放 Item 的 Bucket 的时间是 O(1)。但如果涉及到新增 Cache 或者移除 Cache 等操作，将会导致所有 Item 重新 Hashing，已经存在的缓存内容将会失效。

例如，设 n 为 Cache 的数量，使用最简单的 Linear Hashing 则有：

y = ax + b (mod n)

而当新增一个 Cache 时，Cache 的数量变为 n + 1：

y = ax + b (mod (n+1))

而当移除一个 Cache 时，Cache 的数量变为 n - 1：

y = ax + b (mod (n-1))

当所有的缓存都失效时，新的请求都会抵达 Home 主机，导致 Home 主机崩溃。所以，在处理 Cache 的新增和移除时，较好的效果就是只有少量的 Items 失效。

一致性哈希的性质

一致性哈希（Consistent Hashing）将会从单视角和多视角来看待 Item 和 Bucket 的关系，这使得一致性哈希会满足一些特定的性质。

视角（View）的不一致性（Inconsistent Views）将影响对 Cache 的选择。从用户视角（Client View）来看，每个 Client 只了解一组不同的 Cache 集合。

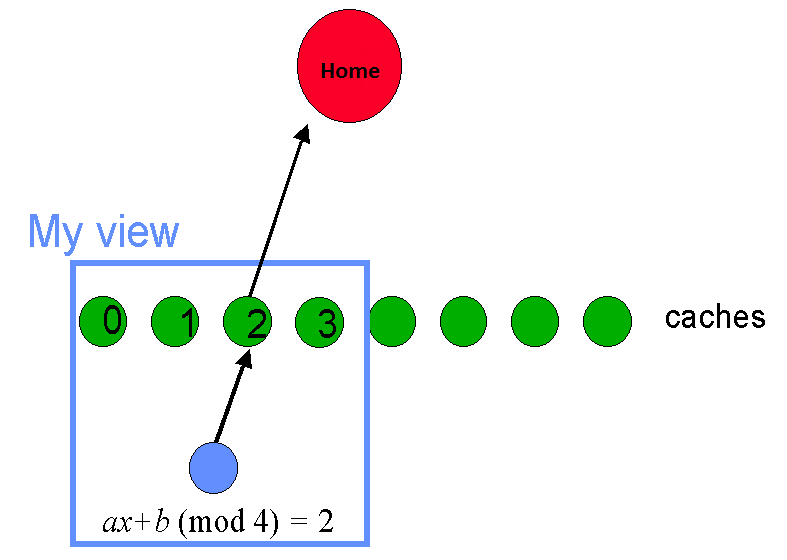
如果 View 特别多，则同一个 Item 可以出现在每个 Cache 上，这样 Home 将会被 Cache 的请求淹没。所以，对于分散 Item 的设计目标是，不管有多少 View，Item 将仅存在于少数 Cache 上。

单视角性质（Single View Properties）

• 平衡（Balance）：所有的 Bucket 都可以获取到大致平均的 Item 数量。
• 平滑（Smooth）：当添加第 k^th 个 Bucket 时，仅会影响所有 Items 中的 1/k 部分，并且仅影响 O(log n) 个服务器。又称为单调性（Monotonicity）。

多视角性质（Multiple View Properties）

假设有 n 个视角，每一个对应到所有 Buckets 的一个任意常量的部分。

• 负载（Load）：任意一个 Bucket 从所有 Views 中所获得的 Items 的数量是 O(log n)，而无论有多少视角，来保证负载的平衡。
• 分散（Spread）：从所有 Views 来看，每一个 Item 将出现在 O(log n) 个 Buckets 中，而无论有多少视角，对于单一的 Item 都将出现在较少的 Buckets 中。

一致性哈希的实现

对所有的 Buckets 和 Items 应用相同的哈希函数 H，按照哈希值的顺序把它们排列到一条线上，然后将距离 Bucket 最近的 Items 都放入该 Bucket 中。

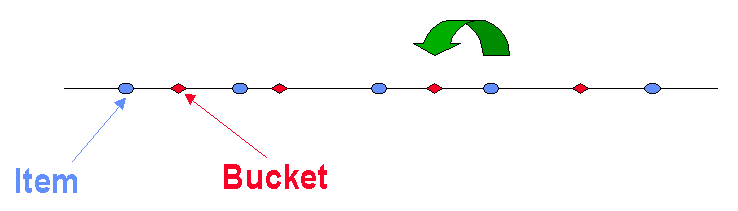
另一种实现方式是把哈希值的最大值和最小值连接到一起，形成一个哈希环（Consistent Hashing Ring），按照顺时针方向将 Items 放入 Bucket 中。

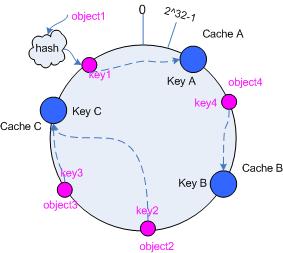
使用哈希函数 H 对 Item 进行计算后，需要找到合适的 Bucket 放入，此时可以选择不同的算法，例如：

• 使用二分查找法为 O(log n)。
• 可以预先计算 Bucket 的哈希，使用额外的哈希表为 O(1)。

平衡（Balance）

如果哈希函数 H 可以将 Bucket 均匀地分布到线上，则每个 Bucket 都拥有线上均等的部分。

同样哈希函数 H 将 Item 也均匀地分布到线上，这样 Item 将等可能地分布到任意的 Bucket 中，所有 Bucket 都能获得均等数量的 Items。

平滑（Smooth）

通常 Bucket 会捕获离其最近的 Items。

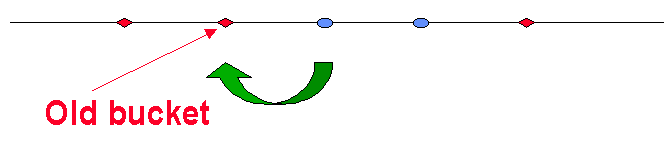
当要添加第 k^th 个 Bucket 时，使用同样的哈希函数 H 将其添加到线上。

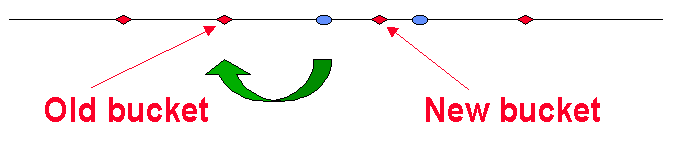
 这样，新的 Bucket 将捕获离其最近的 Items。

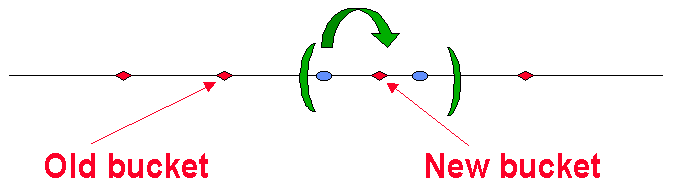
我们发现，在这种条件下：

• 仅有 Items 总数的 1/k 部分会被影响到。
• 仅影响新的 Bucket 左右两边的 2 个 Buckets。

负载（Load）

一个 Bucket 将捕获其附近的 Items，如果 Item 离它是最近的。但 Item 不可能总是离某一个 Bucket 是最近的，则任意一个 Bucket 都不可能捕获特别多的 Items，所以负载是均衡的。

分散（Spread）

对于一个 Item，只有真正离其最近的 Bucket 才会捕获它。在每一个视角中，都只会有一个离其最近的 Bucket，这样对于单一的 Item 都将出现在较少的 Buckets 中。

虚拟节点策略（Virtual Node Strategy）

如果使用的哈希算法 H 并不能保证绝对的平衡性，或者可使用的 Buckets 数量较少时，Items 可能无法被均匀地映射到 Buckets 上。为了解决这种问题，可以在哈希环中引入虚拟节点（Virtual Node）的策略。

虚拟节点（Virtual Node）是实际节点在哈希空间中的复制品（Replica）。一个实际节点可以对应若干个虚拟节点，虚拟节点在哈希空间中使用同样的哈希函数 H 计算哈希值并进行排列。

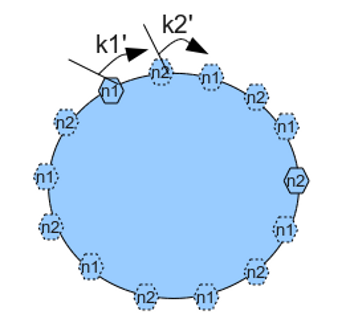
一致性哈希的简单代码实现

首先构建哈希算法的抽象。

  public interface IHashAlgorithm
  {
    int Hash(string item);
  }

向 ConsistentHash<T> 类中注入 IHashAlgorithm 的具体实现。

ConsistentHash<T> 类内实现哈希环，并可以指定虚拟节点的复制因子。

  public class ConsistentHash<T>
  {
    private SortedDictionary<int, T> _ring = new SortedDictionary<int, T>();
    private int[] _nodeKeysInRing = null;
    private IHashAlgorithm _hashAlgorithm;
    private int _virtualNodeReplicationFactor = 1000;

    public ConsistentHash(IHashAlgorithm hashAlgorithm)
    {
      _hashAlgorithm = hashAlgorithm;
    }

    public ConsistentHash(IHashAlgorithm hashAlgorithm, int virtualNodeReplicationFactor)
      : this(hashAlgorithm)
    {
      _virtualNodeReplicationFactor = virtualNodeReplicationFactor;
    }

    public int VirtualNodeReplicationFactor
    {
      get { return _virtualNodeReplicationFactor; }
    }

    public void Initialize(IEnumerable<T> nodes)
    {
      foreach (T node in nodes)
      {
        AddNode(node);
      }
      _nodeKeysInRing = _ring.Keys.ToArray();
    }

    public void Add(T node)
    {
      AddNode(node);
      _nodeKeysInRing = _ring.Keys.ToArray();
    }

    public void Remove(T node)
    {
      RemoveNode(node);
      _nodeKeysInRing = _ring.Keys.ToArray();
    }

    private void AddNode(T node)
    {
      for (int i = 0; i < _virtualNodeReplicationFactor; i++)
      {
        int hashOfVirtualNode = _hashAlgorithm.Hash(node.GetHashCode().ToString() + i);
        _ring[hashOfVirtualNode] = node;
      }
    }

    private void RemoveNode(T node)
    {
      for (int i = 0; i < _virtualNodeReplicationFactor; i++)
      {
        int hashOfVirtualNode = _hashAlgorithm.Hash(node.GetHashCode().ToString() + i);
        _ring.Remove(hashOfVirtualNode);
      }
    }

    public T GetItemNode(string item)
    {
      int hashOfItem = _hashAlgorithm.Hash(item);
      int nearestNodePosition = GetClockwiseNearestNode(_nodeKeysInRing, hashOfItem);
      return _ring[_nodeKeysInRing[nearestNodePosition]];
    }

    private int GetClockwiseNearestNode(int[] keys, int hashOfItem)
    {
      int begin = 0;
      int end = keys.Length - 1;

      if (keys[end] < hashOfItem || keys[0] > hashOfItem)
      {
        return 0;
      }

      int mid = begin;
      while ((end - begin) > 1)
      {
        mid = (end + begin) / 2;
        if (keys[mid] >= hashOfItem) end = mid;
        else begin = mid;
      }

      return end;
    }
  }

然后，我们就可以实现任意一个符合需求的哈希算法，比如如下的 MurmurHash2 算法。

  public class MurmurHash2HashAlgorithm : IHashAlgorithm
  {
    public int Hash(string item)
    {
      uint hash = Hash(Encoding.ASCII.GetBytes(item));
      return (int)hash;
    }

    private const UInt32 m = 0x5bd1e995;
    private const Int32 r = 24;

    public static UInt32 Hash(Byte[] data)
    {
      return Hash(data, 0xc58f1a7b);
    }

    public static UInt32 Hash(Byte[] data, UInt32 seed)
    {
      Int32 length = data.Length;
      if (length == 0)
        return 0;

      UInt32 h = seed ^ (UInt32)length;
      Int32 c = 0; // current index
      while (length >= 4)
      {
        UInt32 k = (UInt32)(
          data[c++]
          | data[c++] << 8
          | data[c++] << 16
          | data[c++] << 24);
        k *= m;
        k ^= k >> r;
        k *= m;

        h *= m;
        h ^= k;
        length -= 4;
      }
      switch (length)
      {
        case 3:
          h ^= (UInt16)(data[c++] | data[c++] << 8);
          h ^= (UInt32)(data[c] << 16);
          h *= m;
          break;
        case 2:
          h ^= (UInt16)(data[c++] | data[c] << 8);
          h *= m;
          break;
        case 1:
          h ^= data[c];
          h *= m;
          break;
        default:
          break;
      }

      // Do a few final mixes of the hash to ensure the last few
      // bytes are well-incorporated.

      h ^= h >> 13;
      h *= m;
      h ^= h >> 15;

      return h;
    }
  }

这样，我们就可以测试该 ConsistentHash<T> 的分布效果了。

  class Program
  {
    static void Main(string[] args)
    {
      List<CacheServer> servers = new List<CacheServer>();
      for (int i = 0; i < 5; i++)
      {
        servers.Add(new CacheServer(i));
      }

      var consistentHashing = new ConsistentHash<CacheServer>(
        new MurmurHash2HashAlgorithm(), 10000);
      consistentHashing.Initialize(servers);

      int searchNodeCount = 10;

      SortedList<int, int> bucketNodes = new SortedList<int, int>();
      for (int i = 0; i < searchNodeCount; i++)
      {
        string item = i.ToString();
        int serverId = consistentHashing.GetItemNode(item).ID;
        bucketNodes[i] = serverId;

        Console.WriteLine("Item[{0}] is in Node[{1}]", i, bucketNodes[i]);
      }

      Console.Read();
    }
  }

  public class CacheServer
  {
    public CacheServer(int serverId)
    {
      ID = serverId;
    }

    public int ID { get; set; }

    public override int GetHashCode()
    {
      return ("CacheServer-" + ID).GetHashCode();
    }
  }

上面代码示例中向一致性哈希环获取给定的 10 个 Items 的顺时针方向的节点，结果如下。

完整代码位置在 Github ：ConsistentHashingDemo。

参考资料

• Consistent hashing and random trees: distributed caching protocols for relieving hot spots on the World Wide Web
• Consistent Hashing: Load Balancing in a Changing World
• Building a Consistent Hashing Ring
• How data is distributed across a cluster using virtual nodes in Cassandra
• Virtual nodes in Cassandra 1.2
• 一致性hash算法 - consistent hashing
• 一致性哈希算法与Java实现
• Consistent hashing
• Consistent hashing on Wikipedia
• 一致性hash 之 [翻译]Consistent Hash By Tom White
• 一致性哈希简单介绍
• 一致性哈希算法（Consistent Hashing）
• 一致性哈希
• memcached全面剖析--4. memcached的分布式算法
• Programmer’s Toolbox Part 3: Consistent Hashing
• Riak : a distributed key-value database
• Akka's consistent hashing router
• Openstack Partitioned Consistent Hash Ring
• Linear hashing
• Fowler–Noll–Vo hash function
• Linear Congruential Generator
• Lehmer Random Number Generator
• 一致性hash算法简介
• 一致性Hash算法(Consistent Hashing)
• 一致性hash和solr千万级数据分布式搜索引擎中的应用
• 每天进步一点点——五分钟理解一致性哈希算法(consistent hashing)
• How automatic sharding works or consistent hashing under the hood
• Consistent hashing in C#
• Consistent Hashing in .NET
• C# SuperFastHash and MurmurHash2 implementations
• Chord (peer-to-peer)
• Hash functions
• MurmurHash2 Statistics

本文《一致性哈希》由 Dennis Gao 发表自博客园博客，任何未经作者本人允许的人为或爬虫转载均为耍流氓。