二项堆
在计算机科学中,二项堆(Binomial Heap)是一种堆结构。与二叉堆(Binary Heap)相比,其优势是可以快速合并两个堆,因此它属于可合并堆(Mergeable Heap)数据结构的一种。
可合并堆通常支持下面几种操作:
- Make-Heap():创建并返回一个不包含任何元素的新堆。
- Insert(H, x):将节点 x 插入到堆 H 中。
- Minimum(H):返回堆 H 中的最小关键字。
- Extract-Min(H):将堆 H 中包含最小关键字的节点删除。
- Union(H1, H2):创建并返回一个包含 H1和 H2 的新堆。
- Decrease-Key(H, x, k):将新关键字 k 赋给堆 H 中的节点 x。
- Delete(H, x):从堆 H 中删除 节点 x。
二项树
一个二项堆由一组二项树所构成,二项树是一种特殊的多分支有序树,如下图 (a)。

二项树 Bk 是一种递归定义的有序树。二项树 B0 只包含一个结点。二项树 Bk 由两个子树 Bk-1 连接而成:其中一棵树的根是另一棵树的根的最左孩子。
二项树的性质有:
- 共有 2k 个节点。
- 树的高度为 k。
- 在深度 d 处恰有
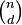 个结点。
个结点。 - 根的度数为 k,它大于任何其他节点的度数;如果根的子女从左到右的编号设为 k-1, k-2, …, 0,子女 i 是子树 Bi 的根。
上图 (b) 表示二项树 B0 至 B4 中各节点的深度。图 (c) 以另外一种方式来看二项树 Bk。
在一棵包含 n 个节点的二项树中,任意节点的最大度数为 lgn。
二项堆
二项堆 H 由一组满足下面的二项堆性质的二项树组成。
- H 中的每个二项树遵循最小堆的性质:节点的关键字大于等于其父节点的关键字。
- 对于任意非负整数 k,在 H 中至多有一棵二项树的根具有度数 k。
第一个性质告诉我们,在一棵最小堆有序的二项树中,其根包含了树中最小的关键字。
第二个性质告诉我们,在包含 n 个节点的二项堆H中,包含至多 floor(lgn)+1 棵二项树。

比如上图中一个包含 13 个节点的二项堆 H。13的二进制表示为(1101),故 H 包含了最小堆有序二项树B3,B2 和 B0, 他们分别有 8,4 和 1 个节点,即共有 13 个节点。
代码示例
1 /* heap.h -- Binomial Heaps 2 * 3 * Copyright (c) 2008, Bjoern B. Brandenburg <bbb [at] cs.unc.edu> 4 * 5 * All rights reserved. 6 * 7 * Redistribution and use in source and binary forms, with or without 8 * modification, are permitted provided that the following conditions are met: 9 * * Redistributions of source code must retain the above copyright 10 * notice, this list of conditions and the following disclaimer. 11 * * Redistributions in binary form must reproduce the above copyright 12 * notice, this list of conditions and the following disclaimer in the 13 * documentation and/or other materials provided with the distribution. 14 * * Neither the name of the University of North Carolina nor the 15 * names of its contributors may be used to endorse or promote products 16 * derived from this software without specific prior written permission. 17 * 18 * THIS SOFTWARE IS PROVIDED BY COPYRIGHT OWNER AND CONTRIBUTERS ``AS IS'' AND 19 * ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE 20 * IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE 21 * ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTERS BE 22 * LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR 23 * CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF 24 * SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS 25 * INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN 26 * CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) 27 * ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE 28 * POSSIBILITY OF SUCH DAMAGE. 29 */ 30 31 #ifndef HEAP_H 32 #define HEAP_H 33 34 #define NOT_IN_HEAP UINT_MAX 35 36 struct heap_node { 37 struct heap_node* parent; 38 struct heap_node* next; 39 struct heap_node* child; 40 41 unsigned int degree; 42 void* value; 43 struct heap_node** ref; 44 }; 45 46 struct heap { 47 struct heap_node* head; 48 /* We cache the minimum of the heap. 49 * This speeds up repeated peek operations. 50 */ 51 struct heap_node* min; 52 }; 53 54 /* item comparison function: 55 * return 1 if a has higher prio than b, 0 otherwise 56 */ 57 typedef int (*heap_prio_t)(struct heap_node* a, struct heap_node* b); 58 59 static inline void heap_init(struct heap* heap) 60 { 61 heap->head = NULL; 62 heap->min = NULL; 63 } 64 65 static inline void heap_node_init_ref(struct heap_node** _h, void* value) 66 { 67 struct heap_node* h = *_h; 68 h->parent = NULL; 69 h->next = NULL; 70 h->child = NULL; 71 h->degree = NOT_IN_HEAP; 72 h->value = value; 73 h->ref = _h; 74 } 75 76 static inline void heap_node_init(struct heap_node* h, void* value) 77 { 78 h->parent = NULL; 79 h->next = NULL; 80 h->child = NULL; 81 h->degree = NOT_IN_HEAP; 82 h->value = value; 83 h->ref = NULL; 84 } 85 86 static inline void* heap_node_value(struct heap_node* h) 87 { 88 return h->value; 89 } 90 91 static inline int heap_node_in_heap(struct heap_node* h) 92 { 93 return h->degree != NOT_IN_HEAP; 94 } 95 96 static inline int heap_empty(struct heap* heap) 97 { 98 return heap->head == NULL && heap->min == NULL; 99 } 100 101 /* make child a subtree of root */ 102 static inline void __heap_link(struct heap_node* root, 103 struct heap_node* child) 104 { 105 child->parent = root; 106 child->next = root->child; 107 root->child = child; 108 root->degree++; 109 } 110 111 /* merge root lists */ 112 static inline struct heap_node* __heap_merge(struct heap_node* a, 113 struct heap_node* b) 114 { 115 struct heap_node* head = NULL; 116 struct heap_node** pos = &head; 117 118 while (a && b) { 119 if (a->degree < b->degree) { 120 *pos = a; 121 a = a->next; 122 } else { 123 *pos = b; 124 b = b->next; 125 } 126 pos = &(*pos)->next; 127 } 128 if (a) 129 *pos = a; 130 else 131 *pos = b; 132 return head; 133 } 134 135 /* reverse a linked list of nodes. also clears parent pointer */ 136 static inline struct heap_node* __heap_reverse(struct heap_node* h) 137 { 138 struct heap_node* tail = NULL; 139 struct heap_node* next; 140 141 if (!h) 142 return h; 143 144 h->parent = NULL; 145 while (h->next) { 146 next = h->next; 147 h->next = tail; 148 tail = h; 149 h = next; 150 h->parent = NULL; 151 } 152 h->next = tail; 153 return h; 154 } 155 156 static inline void __heap_min(heap_prio_t higher_prio, struct heap* heap, 157 struct heap_node** prev, struct heap_node** node) 158 { 159 struct heap_node *_prev, *cur; 160 *prev = NULL; 161 162 if (!heap->head) { 163 *node = NULL; 164 return; 165 } 166 167 *node = heap->head; 168 _prev = heap->head; 169 cur = heap->head->next; 170 while (cur) { 171 if (higher_prio(cur, *node)) { 172 *node = cur; 173 *prev = _prev; 174 } 175 _prev = cur; 176 cur = cur->next; 177 } 178 } 179 180 static inline void __heap_union(heap_prio_t higher_prio, struct heap* heap, 181 struct heap_node* h2) 182 { 183 struct heap_node* h1; 184 struct heap_node *prev, *x, *next; 185 if (!h2) 186 return; 187 h1 = heap->head; 188 if (!h1) { 189 heap->head = h2; 190 return; 191 } 192 h1 = __heap_merge(h1, h2); 193 prev = NULL; 194 x = h1; 195 next = x->next; 196 while (next) { 197 if (x->degree != next->degree || 198 (next->next && next->next->degree == x->degree)) { 199 /* nothing to do, advance */ 200 prev = x; 201 x = next; 202 } else if (higher_prio(x, next)) { 203 /* x becomes the root of next */ 204 x->next = next->next; 205 __heap_link(x, next); 206 } else { 207 /* next becomes the root of x */ 208 if (prev) 209 prev->next = next; 210 else 211 h1 = next; 212 __heap_link(next, x); 213 x = next; 214 } 215 next = x->next; 216 } 217 heap->head = h1; 218 } 219 220 static inline struct heap_node* __heap_extract_min(heap_prio_t higher_prio, 221 struct heap* heap) 222 { 223 struct heap_node *prev, *node; 224 __heap_min(higher_prio, heap, &prev, &node); 225 if (!node) 226 return NULL; 227 if (prev) 228 prev->next = node->next; 229 else 230 heap->head = node->next; 231 __heap_union(higher_prio, heap, __heap_reverse(node->child)); 232 return node; 233 } 234 235 /* insert (and reinitialize) a node into the heap */ 236 static inline void heap_insert(heap_prio_t higher_prio, struct heap* heap, 237 struct heap_node* node) 238 { 239 struct heap_node *min; 240 node->child = NULL; 241 node->parent = NULL; 242 node->next = NULL; 243 node->degree = 0; 244 if (heap->min && higher_prio(node, heap->min)) { 245 /* swap min cache */ 246 min = heap->min; 247 min->child = NULL; 248 min->parent = NULL; 249 min->next = NULL; 250 min->degree = 0; 251 __heap_union(higher_prio, heap, min); 252 heap->min = node; 253 } else 254 __heap_union(higher_prio, heap, node); 255 } 256 257 static inline void __uncache_min(heap_prio_t higher_prio, struct heap* heap) 258 { 259 struct heap_node* min; 260 if (heap->min) { 261 min = heap->min; 262 heap->min = NULL; 263 heap_insert(higher_prio, heap, min); 264 } 265 } 266 267 /* merge addition into target */ 268 static inline void heap_union(heap_prio_t higher_prio, 269 struct heap* target, struct heap* addition) 270 { 271 /* first insert any cached minima, if necessary */ 272 __uncache_min(higher_prio, target); 273 __uncache_min(higher_prio, addition); 274 __heap_union(higher_prio, target, addition->head); 275 /* this is a destructive merge */ 276 addition->head = NULL; 277 } 278 279 static inline struct heap_node* heap_peek(heap_prio_t higher_prio, 280 struct heap* heap) 281 { 282 if (!heap->min) 283 heap->min = __heap_extract_min(higher_prio, heap); 284 return heap->min; 285 } 286 287 static inline struct heap_node* heap_take(heap_prio_t higher_prio, 288 struct heap* heap) 289 { 290 struct heap_node *node; 291 if (!heap->min) 292 heap->min = __heap_extract_min(higher_prio, heap); 293 node = heap->min; 294 heap->min = NULL; 295 if (node) 296 node->degree = NOT_IN_HEAP; 297 return node; 298 } 299 300 static inline void heap_decrease(heap_prio_t higher_prio, struct heap* heap, 301 struct heap_node* node) 302 { 303 struct heap_node *parent; 304 struct heap_node** tmp_ref; 305 void* tmp; 306 307 /* node's priority was decreased, we need to update its position */ 308 if (!node->ref) 309 return; 310 if (heap->min != node) { 311 if (heap->min && higher_prio(node, heap->min)) 312 __uncache_min(higher_prio, heap); 313 /* bubble up */ 314 parent = node->parent; 315 while (parent && higher_prio(node, parent)) { 316 /* swap parent and node */ 317 tmp = parent->value; 318 parent->value = node->value; 319 node->value = tmp; 320 /* swap references */ 321 if (parent->ref) 322 *(parent->ref) = node; 323 *(node->ref) = parent; 324 tmp_ref = parent->ref; 325 parent->ref = node->ref; 326 node->ref = tmp_ref; 327 /* step up */ 328 node = parent; 329 parent = node->parent; 330 } 331 } 332 } 333 334 static inline void heap_delete(heap_prio_t higher_prio, struct heap* heap, 335 struct heap_node* node) 336 { 337 struct heap_node *parent, *prev, *pos; 338 struct heap_node** tmp_ref; 339 void* tmp; 340 341 if (!node->ref) /* can only delete if we have a reference */ 342 return; 343 if (heap->min != node) { 344 /* bubble up */ 345 parent = node->parent; 346 while (parent) { 347 /* swap parent and node */ 348 tmp = parent->value; 349 parent->value = node->value; 350 node->value = tmp; 351 /* swap references */ 352 if (parent->ref) 353 *(parent->ref) = node; 354 *(node->ref) = parent; 355 tmp_ref = parent->ref; 356 parent->ref = node->ref; 357 node->ref = tmp_ref; 358 /* step up */ 359 node = parent; 360 parent = node->parent; 361 } 362 /* now delete: 363 * first find prev */ 364 prev = NULL; 365 pos = heap->head; 366 while (pos != node) { 367 prev = pos; 368 pos = pos->next; 369 } 370 /* we have prev, now remove node */ 371 if (prev) 372 prev->next = node->next; 373 else 374 heap->head = node->next; 375 __heap_union(higher_prio, heap, __heap_reverse(node->child)); 376 } else 377 heap->min = NULL; 378 node->degree = NOT_IN_HEAP; 379 } 380 381 #endif /* HEAP_H */


