排序算法之冒泡排序

   

举一隅不以三隅反，则不复也 ------孔子

前言

冒泡排序是常用排序算法之一，基于冒泡排序的扫描交换思想在其它程序设计中是一种很常用的设计思想。本篇文章从什么是有序序列说起，进而讲解扫描交换的思想，以实例带领读者理解冒泡排序的设计机理，使读者能够见微知著，体会到不一样的思路，更能够做到举一反三。

从有序序列说起

DS是数据项的结构化集合，其结构性体现在数据项之间的相互性和作用上。具体说就是数据项之间的逻辑次序。而序列作为一种最基本的线性结构，其实现机理需要我们掌握好。排序作为处理数据项之间大小关系的算法，有着广泛应用。在序列中，怎样评判一个序列是有序的呢？比如序列A{1 2 3 4 5}，我们一目了然其实有序排序的（sorted sequence），而序列B{3 2 4 1 5}是无序序列（unsorted sequence）。认真观察不难发现，序列A中任意一对相邻的元素对都是顺序的（有序的）如相邻元素对1 2 、2 3、 3 4 、4 5都是顺序的；序列B中存在相邻的元素对是逆序对，如3 2 、4 1。也就是说，在序列中，如果任意一对相邻元素对都是顺序的，那么该序列是有序序列；反之，如果总有一对相邻元素对是逆序的，那么该序列就是逆序的。这个结论浅显易懂，但是给我们接下来分析提供了思路。

扫描交换思想

扫描就是顺序比较每一对相邻元素对，如果它们是逆序对，那就交换两个元素之间的顺序使其成为顺序对。而冒泡排序Bubblesort就是基于扫描交换实现对序列的排序。在长度为n的序列A中，初始时假设sorted=true；即认为该序列无序，然后在第1趟扫描过程中，如果发现相邻逆序对（A[i]>A[i+1]），就交换swap(A[i],A[i+1])使其成为相邻顺序对，这样一趟扫描序列之后，最大元素肯定处在A[n-1]，即一趟扫描之后，无序序列长度变为n-1。在第k趟扫描之后，第k大元素已经就绪在A[n-k-1]，无序序列长度变为n-k。通过一趟扫描交换使原问题规模由n变为n-1，这就是减治策略。

代码实现

实现算法1

  1. void bubblesort(int A[],int n) //冒泡排序A[0 n)
  2. {
  3.    for(bool sorted=false; sorted=!sorted; n--) //反复扫描交换，每一趟之后原问题规模就减1
  4.    {
  5.       for(int j=1;j<n;j++)//从左向右，逐对检查A[0,n)内各个相邻元素对
  6.       {
  7.          if(A[j-1]>A[j]) //如果发现相邻逆序对
  8.          {
  9.             swap(A[j-1],A[j]); //交换
  10.             sorted=false; //同时清除全局有序标志
  11.          }
  12.       }
  13.    }
  14. }

分析：根据减治法，外层循环不断缩减待排序列长度，同时置全局有序标志为true；在第k趟扫描中，内层循环处理n-k个元素，进行n-k-1次比较；若在一趟扫描中没有发现逆序对，则全局标志没有被赋值false，此时外层循环就跳出结束。

算法的基本步骤就是相邻元素对的比较以及交换。时间复杂度为O(n2),在最好情况下，序列已经有序，则完成一趟扫描交换即结束O(n)，最坏情况下，序列完全逆序排序，第k趟扫描交换需要比较n-k-1次，进行n-k-1次交换，时间复杂度O(n2)

基于代码实现1我们可以将扫描算法和冒泡排序算法分离，形成如下代码

实现算法2

  1. void bubblesort(int A[],int lo,int hi) //冒泡排序 A[lo,hi)左闭右开区间
  2. {
  3.    while(!(bubble(A,lo,hi--))); //进行扫描交换，直至全序
  4. }
  5. bool bubble(int A[],int lo,int hi)// 扫描交换 A[lo,hi)
  6. {
  7.    bool sorted=true;
  8.    while(++lo<hi) //从左向右，逐一检查各对相邻元素
  9.    {
  10.       if(A[lo-1]>A[lo])
  11.       {
  12.          swap(A[lo-1],A[lo]);
  13.          sorted=false;
  14.       }
  15.    }
  16.    return sorted;
  17. }

运行结果

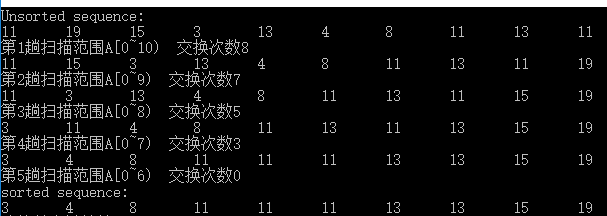
优化策略

对于上述两个实现方式，如果对于A[0,n]，乱序仅限于A[ 0, )，则其前缀和后缀长度相差悬殊，基于此，首先它会作第一趟扫描，并且确认在最后这个位置有一个元素已经就位（这个元素本来就是就位的）,在后缀中，存在着大量就位元素，但因为前缀中存在着交换，bubble会返回false，即算法接下来还会继续扫描下去，直到前缀已经完全有序。而在这些扫描中，本来后缀应该不必要扫描了，因为其已经有序就位了，但是仍然需要扫描交换r次（r为前缀长度= ）。这个算法整体消耗时间O(n*r)=O(),应该改进它使其为O(n)

 如举例序列A={4,3,2,1,5,6,7,8,9,10}

运行结果如下

代码实现3（改进版）

  1. void bubblesort(int A[],int lo,int hi)// 冒泡排序A[lo,hi)
  2. {
  3.    while(lo<(hi=bubble(A,lo,hi)));//逐趟扫描交换，直至全序
  4. }
  5. int bubble(int A[],int lo,int hi)//扫描交换 A[lo,hi) 返回最后一个逆序对的下标
  6. {
  7.    int last=lo; //最右侧逆序对下标
  8.    while(++lo<hi) //自左向右，逐一检查各对相邻元素
  9.    {
  10.       if(A[lo-1]>A[lo]) //如果逆序
  11.       {
  12.          last=lo; //更新最右侧逆序对位置记录
  13.          swap(A[lo-1],A[lo]); //并交换
  14.       }
  15.    }
  16.    return last; //返回最右侧逆序对位置
  17. }

更改之后的算法遇到乱序仅限于A[ 0, )，只需要O( n + O( 2 ) )=O(2n)=O(n)时间，而且第一趟扫描之后，序列区间就缩小为乱序的前缀，不会再依次比较后缀中已然有序的元素了，看来有很大改进了。

运行效果对比（可以看到改进版本对于乱序和有序长度差别极大的序列有很大的算法优化，比较次数变得很少）

总结

冒泡排序是根据减治法策略，依托扫描算法来实现序列的排序，其最坏时间复杂度和平均时间复杂度都为O(n2)，而最好时间复杂度为O(n)。根据其实现算法，冒泡排序是稳定排序，因为bubblesort中对元素位置唯一调整的可能就是某元素A[i-1]严格大于其直接后继元素A[i]，在这种亦步亦趋地交换过程中，重复元素虽然可以相互靠拢，但是绝对不会相互跨越，因此bubblesort属于稳定排序算法。

小计：

稳定排序算法有：bubblesort（冒泡排序）、insertionsort（插入排序）、mergesort（归并排序）、radixsort（基数排序）

不稳定排序算法有：shellsort（希尔排序）selectionsort（选择排序）quicksort（快速排序）heapsort（堆排序）

posted @ 2018-07-01 22:11  聊寂园  阅读(1516)  评论(0)  编辑  收藏  举报