容器扩容之分摊时间复杂度分析
以向量vector为例分析动态扩容算法设计和时间复杂度分析
扩容算法实现
如何实现扩容,新的容量取多少合适?
对于容器内部数据区为数组的容器来说,动态扩容是必须的,因为无法预测容器规模的增长,而且必须保证数据区不仅在逻辑上连续分布存储,循秩访问,更要保证其在物理地址上的连续,因此每次插入操作前都需要询问是否需要扩容?

如图2.1(c~e)我们需要申请一个更大容量的连续物理地址作为新的数据区域如数组B【】,然后将原数组的数据复制到新数据区域中(图d),此时才可以插入新元素e,最后,原数据区域的空间地址一定要释放掉归还给操作系统。
一种可行的算法实现如下
-
void Vector<T>::expand() //向量空间不足时扩容
-
{
-
if(_size<_capacity) //尚未满员时,不必扩容
-
return ;
-
if(_capacity<DEFAULT_CAPACITY) //不低于最小容量
-
_capacity=DEFAULT_CAPACITY;
-
T * _oldelem=_elem;
-
_elem=new T[_capacity<<1]; //容量加倍
-
for(int i=0;i<_size;i++) //复制原向量内容(T为基本类型,或者已经重载过"="运算符的自定义类型)
-
_elem[i]=_oldelem[i];
-
delete []oldelem; //释放原空间
-
}
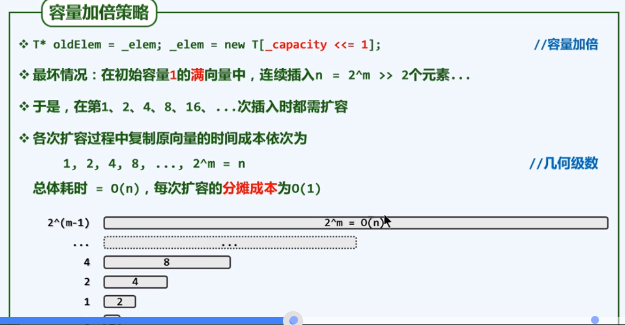
由上述算法实现可以知道,新数组容量扩容至原数组容量的2倍!!
分摊分析
时间代价
可扩充向量和常规数组相比,其更加灵活,容量不受初始容量的限制,但是需要付出代价。插入操作的时间,在最坏情况下,每次扩容都是由n~2n,需要花费O(n)时间,看起来插入效率好像被拉低了,但是这是错觉。 按照约定,每花费O(n)时间实施一次扩容,数组容量都会加倍,这意味着至少再需要经过n次插入操作,才会因为可能移除而在此扩容。即随着向量规模不断扩大,在执行插入操作过程之前需要进行扩容的概率将迅速降低,在某种平衡意义而言,用于扩容的时间成本不至于很高-----下面就是分摊时间复杂度的分析
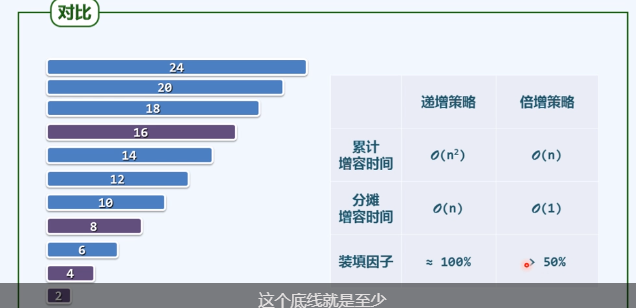
分摊复杂度
对可扩充向量足够多次连续操作,并将期间所消耗的时间,分摊至所有的操作。如此分摊平均至每次操作的时间成本,称为分摊运行时间(amortized running time)。注意与平均时间复杂度(average running time)的区别:后者按照某种假定的概率分布,对各种情况下所需执行时间进行加权平均,也成为期望运行时间(expected running time)。而前者要求,参与分摊的操作必须构成和来自于一个真实可行的操作序列,而且该序列必须足够长。 相对而言,分摊复杂度可以针对计算成本和效率做出更为客观而准确的估计。
O(1)分摊时间
考察连续n次(查询,插入,删除等)操作,将所有的操作中用于数组扩容的时间累加起来,除以n,只要n足够大,这一事件就是用于扩容处理的分摊时间成本。
假定数组初始容量为某一常数N,既然是估计复杂度上界,古设向量初始规模为N----即将溢出。不难知道,除插入操作之外,其他操作都不会导致溢出,考察最坏情况下,假设此之后连续n此操作都是insert,n>>N,定义如下函数
- 1 size(n)=连续插入n个元素之后的向量规模
- 2 capacity(n)=连续插入n个元素之后向量容量
- 3 T(n)=为连续插入n个元素而花费的扩容时间
向量规模从N开始随着操作的继承逐步递增:size(n)=n+N
既然不至于溢出,load factor 装填因子不超过100%,算法扩容采用惰性策略,只有在的确发生溢出状况下才容量加倍,即装填因子始终不低于50%
即可得如下关系式
Size(n)<=capacity(n)<2*size(n)
考虑N为常数 有capacity(n)=O(size(n))=O(n)
容量以2位比例按指数速度增长,在容量达到capacity(n)之前,共做过O(logn)次扩容,每次扩容所需时间现行正比于当时容量,且同样以2为比例按照指数增长。因此,消耗在扩容的时间累计:
T(n)=2N+4N+8N+…+capacity(n)<2capacity(n)=O(n)
将其分摊到其间的连续操作n次,单次操作所需的分摊运行时间应该为O(1)