动态规划求解0/1背包问题

     

问题

给定n种物品和一个背包，物品(1<=i<=n)重量是w_I ，其价值v_i, 背包容量为C,对每种物品只有两种选择：装入背包和不装入背包，即物品是不可能部分装入，部分不装入。如何选择装入背包的物品，使其价值最大？

想法

该问题是最优化问题，求解此问题一般采用动态规划（dynamic plan），很容易证明该问题满足最优性原理。

动态规划的求解过程分三部分：

一：划分子问题：将原问题划分为若干个子问题，每个子问题对应一个决策阶段，并且子问题之间具有重叠关系

二：确定动态规划函数：根据子问题之间的重叠关系找到子问题满足递推关系式（即动态规划函数），这是动态规划的关键

三：填写表格：设计表格，以自底向上的方式计算各个子问题的解并填表，实现动态规划过程。

     

思路：

如何定义子问题？0/1背包可以看做是决策一个序列（x1,x2,x3,…,xn）,对任何一个变量xi的决策时xi=1还是xi=0. 设V(n,C)是将n个物品装入容量为C的背包时背包所获得的的最大价值，显然初始子问题是将前i个物品装如容量为0的背包中和把0个物品装入容量为j的背包中，这些情况背包价值为0即

    V(i,0)=V(0,j)=0 0<=i<=n, 0<=j<=C

     

接下来考虑原问题的一部分，设V(I,j)表示将前i个物品装入容量为j的背包获得的最大价值，在决策xi时，已经确定了(x1,x2,…,xi-1)，则问题处于下列两种情况之一：

1. 背包容量不足以装入物品i，则装入前i-1个物品的最大价值和装入前i个物品最大价值相同，即xi=0，背包价值没有增加
2. 背包容量足以装入物品i， 如果把物品i装入背包，则背包物品价值等于把前i-1个物品装入容量为j-wi的背包中的价值加上第i个物品的价值vi；如果第i个物品没有装入背包，则背包价值等于把前i-1个物品装入容量为j的背包中所取得的价值，显然，取二者最大价值作为把物品i装入容量为j的背包中的最优解，得到如下递推公式

        

为了确定装入背包中的具体物品，从V(n,C)的值向前推，如果V（n，C）>V(n-1,C),

则表明第n个物品被装入背包中，前n-1个物品被装入容量为C-wn的背包中；否则，第n个物品没有被装入背包中，前n-1个物品被装入容量为C的背包中，依次类推，直到确认第一个物品是否被装入背包中

     

代码C++实现

1. // dp_01Knapsack.cpp : 定义控制台应用程序的入口点。
2. #include<iostream>
3. #include<algorithm>
4. using namespace std;
5. const int N = 5;
6. const int Capacity = 20;
7. int flag[N+1] = { 0 };//物品是否在背包中，下标从1开始算
8. int V[N+ 1][Capacity + 1] = { 0 }; //造表记录子问题的最优解
9. int Knapsack(int w[], int v[], int n, int C);//实际物品数目，背包容量
10. int main()
11. {
12.    int w[] = {0,3,2,1,4,5};
13.    int v[] = { 0,25,20,15,40,50 };
14.    int n = 5, C = 6;
15.    int maxValue = Knapsack(w, v, n, C);
16.    cout << maxValue;
17.     return 0;
18. }
19. int Knapsack(int w[], int v[], int n, int C) {
20.    for (int i = 0; i <= n; ++i)
21.       V[i][0] = 0;
22.    for (int j = 0; j <= C; ++j)
23.       V[0][j] = 0;
24.    for(int i=1;i<=n;++i)
25.       for (int j = 1; j <= C; ++j)
26.       {
27.          if (j < w[i])
28.             V[i][j] = V[i - 1][j];
29.          else {
30.             V[i][j] = max(V[i - 1][j], V[i - 1][j - w[i]] + v[i]);
31.          }
32.       }
33.      
34.    for (int i = n, j = C; i > 0; --i)
35.    {
36.       if (V[i][j] > V[i - 1][j])
37.       {
38.          flag[i] = 1;
39.          j -= w[i];
40.       }
41.       else
42.          flag[i] = 0;
43.    }
44.    cout << "造表\n";
45.    for (int i = 0; i <= n; ++ i)
46.    {
47.       for (int j = 0; j <= C; ++j)
48.          cout << V[i][j] << '\t';
49.       cout << endl;
50.    }
51.      
52.    for (int i = 1; i <= n; ++i)
53.       cout << flag[i] << '\t';
54.    cout << endl;
55.    return V[n][C];
56. }

     

结果如下：

     

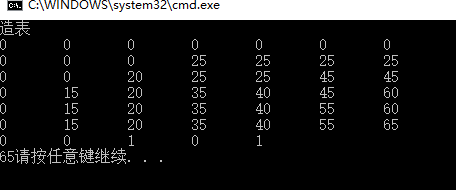
表格分析如下

		0	1	2	3	4	5	6	flag
	0	0	0	0	0	0	0	0
W1=3,v1=25	1	0	0	0	25	25	25	25	0
W2=2,v2=20	2	0	0	20	25	25	45	45	0
W3=1,v3=15	3	0	15	20	35	40	45	45	1
W4=4,v4=40	4	0	15	20	35	40	55	60	0
W5=5,v5=50	5	0	15	20	35	40	55	65	1

   

   

算法性能分析：

在算法Knapsack中，第一个for循环的时间性能是O(n),第二个for循环的时间性能是O(C),第三个循环是两层嵌套for循环，时间性能是O(n*C)，第四个for循环时间性能是O(n);

因此算法时间复杂度O(n*C)