5月5日离散课笔记
生成函数
用来高效的表示序列,把序列的每一项都表示成x的系数
1/(1-x) 1+x+x2+....
多项式的除法
级数
1/(1-x)2呢?
级数的方法:对1/(1-x)求导即是,1+2x+3x+4x+.....,正自然数序列
同样1/(1-x)3也可以用这种方法来求,(K+1)(K+2)/2
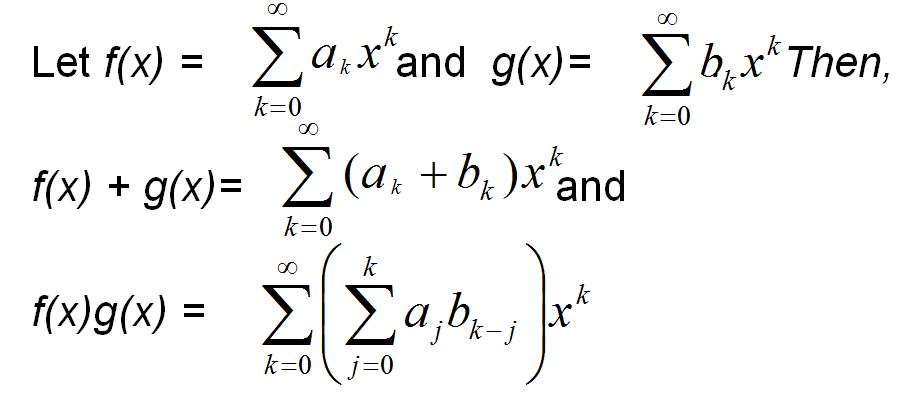
上面就是生成函数加法和乘法的系数公式了
把下面每一个都做了:
0,2,2,2,2,2,2,0,0,0,0…..
0,0,0,1,1,1,1,….
0,1,0,0,1,0,0,1,0,0,1,…
2,4,8,16,32,64,128,256,…
2,-2,2,-2,2,-2,2,-2,……
1,1,0,1,1,1,1,…
0,0,0,1,2,3,4,…
Extended Binomial Coefficients(扩展二项式定理)

EBC(-n,r)= (-n)(-n-1)….(-n-r+1)/r! = (-1)rn(n+1)…(n+r-1)/r! = (-1)r(n+r-1)!/(r!*(n-1)!). Therefore

从而推导出这么漂亮的形式:
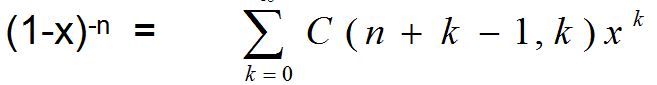
一类问题:N个物体,挑出K个来
1.不重复
(x0 + x1 )(x0 + x1 )(x0 + x1 )(x0 + x1 ).......n个相乘
求出xk 的系数
2.允许重复
(x0 + x1 +x2...........)(x0 + x1 +x2...........)(x0 + x1 +x2...........)(x0 + x1 +x2...........)............n个相乘
写成无穷多项还是具体个数项?

上次作业的生成函数解法
Recurrence Relations
凑出递归式的的形式。。。。,注意这一题
an=8an-1+10n-1, a1=9.(a0 =1)
错排问题,容斥原理

最后附上这次的作业:(不知道对不对啊)



