变分贝叶斯推断

变分原理

《动态最优化基础》中关于泛函和变分的推导。

Euler-Lagrange方程:

\[F_y-\dfrac{d}{dt}F_{y^\prime}=0 \]

或者

\[\dfrac{\partial F}{\partial y}-\dfrac{d}{dx}\dfrac{\partial F}{\partial y^\prime}=0 \]

\(F[t,y(t),y^\prime(t)]\) 表示“弧值”的一般表达式
\(F[t,y(t),y^\prime(t)]dt\) 表示t处的一段微小“弧值”
\(V[y]=\int_0^T F[t,y(t),y^\prime(t)]dt\) 表示“弧值之和”

“弧值”的含义可以是距离、时间、质量、概率等等。

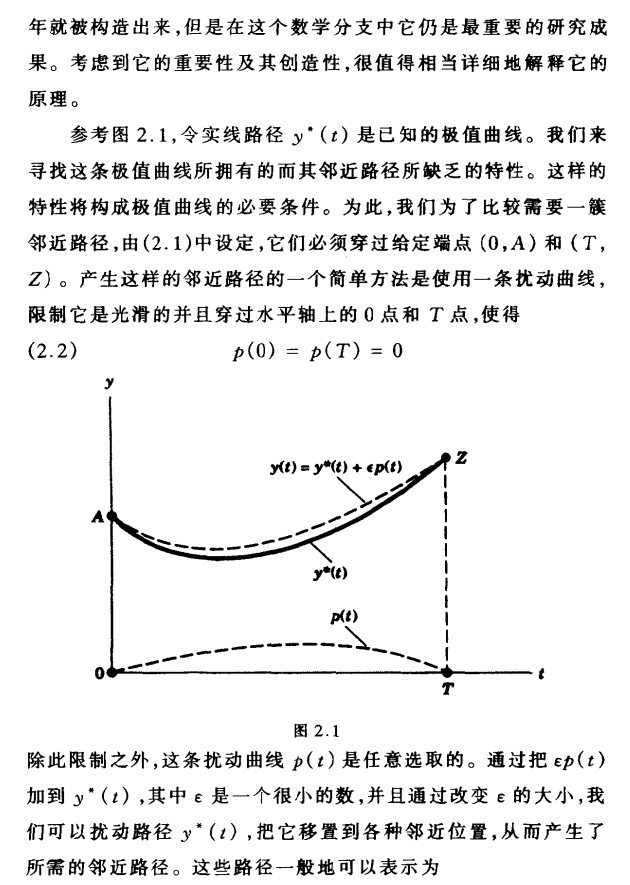
例，连接两点间的最短曲线
现在要找到“最短曲线”，意味着我们需要关于弧值为长度的一个泛函。
两点间长度的一般表达式 \(S=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\)
曲线 \(y(x)\) 上任意相邻的两点 \((x,y),(x+dx,y+dy)\) 微小“弧值”为:

\[\begin{aligned} F[x,y(x),y^\prime(x)]dx &=\sqrt{dx^2+dy^2} =\sqrt{1+(\dfrac{dy}{dx})^2}dx\\ &=\sqrt{1+{y^\prime}^2}dx \end{aligned} \]

设曲线的两端点为 \((a, m)\) 和 \((b, n)\) 则“弧值之和”

\[V[y]=\int_a^b{\sqrt{1+{y^\prime}^2}dx}, F=\sqrt{1+{y^\prime}^2} \]

由Euler-Lagrange方程: \(\dfrac{\partial F}{\partial y}-\dfrac{d}{dx}\dfrac{\partial F}{\partial y^\prime}=0\)

F中不包含y, 有 \(\dfrac{\partial F}{\partial y}=0\)， \(\dfrac{\partial F}{\partial y^\prime}=\dfrac{y^\prime}{\sqrt{1+{y^\prime}^2}}\) 代入欧拉方程：

\[\dfrac{d}{dx}\dfrac{\partial F}{\partial y^\prime}=\dfrac{d}{dx}(\dfrac{y^\prime}{\sqrt{1+{y^\prime}^2}})=0 \]

所以 \(\dfrac{y^\prime}{\sqrt{1+{y^\prime}^2}}=C\)常数，求得 \(y^\prime=C\), 然后对 \(y^\prime\) 求积分有：

\[y=kx+c \]

变分贝叶斯推断

变分推理的目标是近似潜在变量(latent variables)在观测变量（observed variables）下的条件概率。解决该问题，需要使用优化方法。在变分推断中，需要使用到的一个重要理论，是平均场理论.

平均场理论

来源于物理学，是一种研究复杂多体问题的方法，将数量巨大的互相作用的多体问题转化成每一个粒子处在一种弱周期场中的单体问题。
对于概率模型：

\[P(x_1,x_2,x_3,\cdots,x_n)=P(x_1)P(x_2|x_1)P(x_3|x_2,x_1) \cdots P(x_n|x_{n-1},\cdots,x_1) \]

可以找到一个近似模型：

\[Q(x_1,x_2,\cdots,x_n)=Q(x_1)Q(x_2)\cdots Q(x_n) \]

使得 Q 与 P 尽可能相似。

在贝叶斯模型中, 通常需要从已知的样本中推测模型的参数，即后验概率 \(P(Z|X)\), 然而直接计算出\(P(Z|X)\)通常比较困难。我们可以利用平均场理论，通过模型 \(Q(Z)=\prod_i Q(z_i)\) 来近似代替 \(P(Z|X)\)。
衡量两个概率密度函数(PDF)的差异，可以利用KL散度(KL-Divergence)。

\[KL(Q(Z)||P(Z|X))=\int Q(Z) log \dfrac{Q(Z)}{P(Z|X)}dZ \]

这里 \(KL(Q(Z)||P(Z|X))\) 即是关于 Q 的泛函。为使 Q 和 P 尽可能相似，则需要KL最小化。
求解KL最小化下，Q 的概率密度函数，即变分问题。其中 Q 的累积分布函数(CDF) \(\int Q(Z)dz =1\) 。

\[KL(Q(Z)||P(Z|X))=\int Q(Z) log \dfrac{Q(Z)}{P(Z|X)}dZ \\ \overset{\text{log取倒数}}{=}-\int Q(Z) log \dfrac{P(Z|X)}{Q(Z)}dZ \\ \overset{\text{上下乘P(Z)}}{=}-\int Q(Z) log \dfrac{P(Z,X)}{Q(Z)P(X)}dZ \\ \overset{\text{log分式展开}}{=}\int Q(Z) [logQ(Z)+logP(Z)]dZ - \int Q(Z)logP(Z,X)dZ \\ \overset{\text{P(X)为常数,Q累积分布为1}}{=}logP(X)+\int Q(Z) logP(Z)dZ - \int Q(Z)logP(Z,X)dZ \\ \]

令\(L(Q)=-[\int Q(Z) logP(Z)dZ - \int Q(Z)logP(Z,X)dZ]\), 则有

\[KL(Q(Z)||P(Z|X))=logP(X)-L(Q) \geq 0 (吉布斯不等式)\\ logP(X) \geq L(Q) \]

\(logP(X)\)的下界\(L(Q)\), 称为 ELOB (Evidence Lower Bound), 其中\(logP(X)\)为常数，通过最大化ELOB \(L(Q)\) 使得KL最小化。求解最大化\(L(Q)\)的过程同样也是一个变分问题。

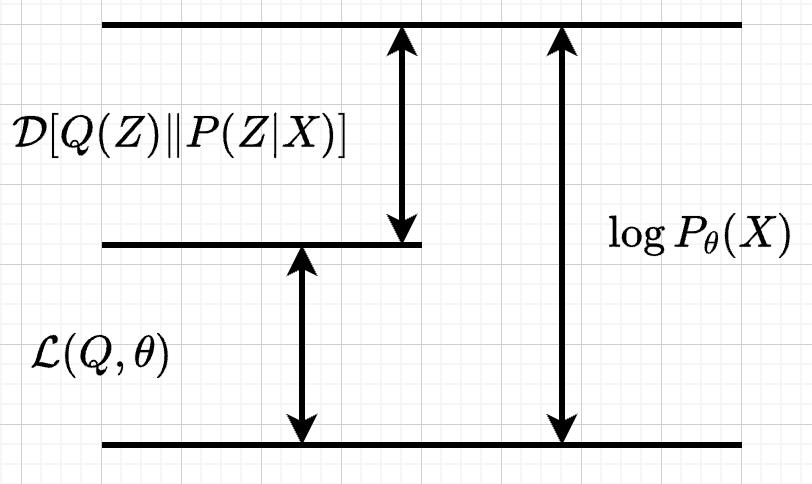
把平均场定理：\(Q(Z)=\prod_i Q(z_i)\) 代入 \(L(Q)\) 中得到：

\[L(Q)=\prod_{i;i\neq j}H(Q(z_i))-KL(Q(z_j)||Q^*(z_j))-C \]

其中\(Q^*(z_j)=\dfrac{exp(E_{i\neq j}[logP(Z,X)])}{\int exp(E_{i\neq j}[logP(Z,X)])}\), 归一化项 \(\int exp(E_{i\neq j}[logP(Z,X)])\) 使得整体的\(Q^*(z_j)\) PDF积分为1。详细推理过程参考变分贝叶斯推断(Variational Bayes Inference)简介

因为信息熵\(\prod_{i;i\neq j}H(Q(z_i))\geq 0, 且 KL(Q(z_j)||Q^*(z_j)) \geq 0\)
所以最大化\(L(Q)\)只需令\(KL(Q(z_j)||Q^*(z_j))=0\), 则有：

\[Q(z_j) = Q^*(z_j) \]

至此，变分贝叶斯推断的通用公式求法，如下：