Pytorch 实现 GAN 网络
Pytorch 实现 GAN 网络
原理
GAN的基本原理其实非常简单,假设我们有两个网络,G(Generator)和D(Discriminator)。它们的功能分别是:
G 是一个生成网络,它接收一个随机的噪声z,通过这个噪声生成伪造数据,记做 G(z)。
D 是一个判别网络,判别数据是不是“真实的”。它的输入参数是x,输出记为 D(x) 代表 x 为真实的概率。如果为 1 就代表 x 为真的概率是100%,而输出为 0 代表为真概率是0% 即为假。
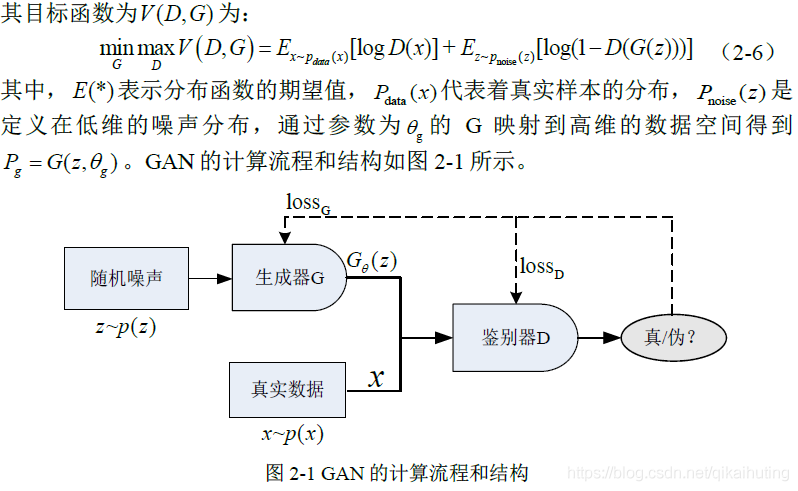
在训练过程中,生成网络 G 的目标就是尽量生成真实的数据去欺骗判别网络D。而 D 的目标就是尽量把 G 生成的数据和真实的数据分别开来。这样,G 和 D 构成了一个动态的“博弈过程”。
最后博弈的结果是什么?在最理想的状态下,G可以生成足以“以假乱真”的数据 G(z) 。对于 D 来说,它难以判定 G 生成的数据究竟是不是真实的,因此 D(G(z)) = 0.5。
当判别器真假难辨时,D_fake,D_real->0.5,G_loss=log(1-0.5)=0.6931..., 此时 D_loss=log(1-0.5)+log(0.5)= 1.3832...
实现
这里我们的任务是:构造一个GAN网络,希望 生成器 能够输入噪声生成一个二次函数曲线
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
BATCH_SIZE = 64
G_IN_SIZE = 15 #生成器 输入尺寸
G_OUT_SIZE = 15 #生成器 输出尺寸
PAINT_POINTS = np.vstack([np.linspace(-1,1, G_OUT_SIZE) for _ in range(BATCH_SIZE)]) #shape (BATCH_SIZE, G_OUT_SIZE)
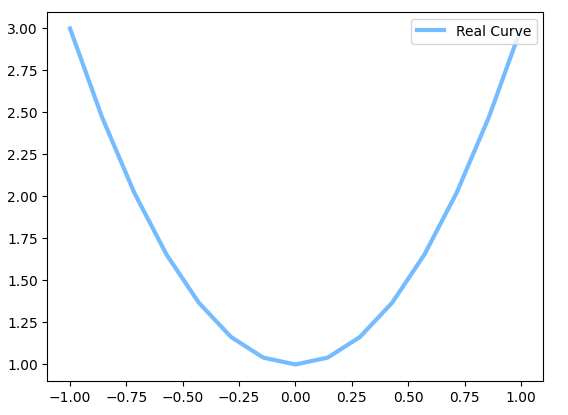
plt.plot(PAINT_POINTS[0], 2 * np.power(PAINT_POINTS[0], 2) + 1, c='#74BCFF', lw=3, label='Real Curve') #2 * x^2 + 1
plt.legend(loc='upper right') #标签位置
plt.show()
# 准备真实数据
def real_points():
paints = 2 * np.power(PAINT_POINTS,2) + 1
paints = torch.from_numpy(paints).float()
return paints
#定义网络
G = nn.Sequential(
nn.Linear(G_IN_SIZE,128),
nn.ReLU(),
nn.Linear(128,G_OUT_SIZE)
)
D = nn.Sequential(
nn.Linear(G_OUT_SIZE,128),
nn.ReLU(),
nn.Linear(128,1),
nn.Sigmoid() #0为False,1为True D的评估应该是在【0-1】之间的数值,所以这里采用的是Sigmod激活
)
# 优化函数
optimizer_G = torch.optim.Adam(G.parameters(),lr=0.0001)
optimizer_D = torch.optim.Adam(D.parameters(),lr=0.0001)
bceloss = nn.BCELoss()
#训练
for step in range(10001):
real_data = real_points() # 生成真实数据
# print('real_data', real_data.shape)
randn_input = torch.randn(BATCH_SIZE, G_IN_SIZE) #输入噪声
# print('randn_input', randn_input.shape)
eps = 1e-6 #防止log 0
D_real = D(real_data) # 0为False,1为True,这里输入真实数据,D_real越靠近1越好
D_fake = D(G(randn_input))
#训练判别器D,根据公式 D_loss 分为两个部分:判断真实数据 log(1-D_real);判断假数据 log(D_fake)
# D带着G一起更新,使用D(G(input))
# D_loss = -torch.mean(torch.log(eps + 1.0 - D_real) + torch.log(eps + D_fake))
D_loss = bceloss(1-D_real, torch.ones_like(D_real)) + bceloss(1-D_fake, torch.zeros_like(D_fake))
optimizer_D.zero_grad()
D_loss.backward()
optimizer_D.step()
#训练生成器G
G_fake_out = G(randn_input) # 生成器生成假数据
D_fake = D(G_fake_out) # 用判别器判别假数据,最好能让判别器判断概率趋近0.5,即生成器生成的假数据,能让判别器真假难辨
# G的损失 越接近1越好,当D_fake->0.5时,G_loss=log(1-0.5)=0.6931..., 此时 D_loss=log(1-0.5)+log(0.5)= 1.3832...
# G_loss = -torch.mean(torch.log(1.0 - D_fake + eps))
G_loss = bceloss(D_fake, torch.zeros_like(D_fake))
optimizer_G.zero_grad()
G_loss.backward() #反向
optimizer_G.step() #更新G参数
if step % 1000 == 0: # plotting
plt.cla()
plt.plot(PAINT_POINTS[0], G_fake_out.data.numpy()[0], c='#4AD631', lw=3, label='Generated Curve',)
plt.plot(PAINT_POINTS[0], 2 * np.power(PAINT_POINTS[0], 2) + 1, c='#74BCFF', lw=3, label='Real Curve')
plt.text(-1.0, 0.4, 'G_loss= %.3f ' % G_loss.data.numpy(), fontdict={'size': 13})
plt.text(-1.0, 0.2, 'D_loss= %.3f ' % D_loss.data.numpy(), fontdict={'size': 13})
plt.ylim((0, 3));plt.legend(loc='upper right', fontsize=10);plt.draw();plt.pause(0.1)

GAN网络的损失函数
另外的,GAN网络的损失函数也可以使用 BCELoss(Binary Cross Entropy Loss) 或 BCEWithLogitsLoss
BCELoss的解释如下:

为了解决无穷的问题,当log小于-100时,固定输出-100.
reduction 默认 mean,x 为 D预测值,y 为实际值(0, 1),则有 loss(x, y) = - mean(y * log(x) + (1-y) * log(1-x))
又因 \(x\in(0,1)\) 所以 log(x)<0, log(1-x)<0, mean前加上负号,使得 loss(x, y) > 0
由图一公式 $ \mathop{min}\limits_{G}\mathop{max}\limits_{D} V(G,D)=E_{x \sim real}[log(D(x))]+E_{z \sim noize}[log(1-D(G(z)))]$ 可知, G 的 目标越小越好, D 的 目标越大越好。

只对G网络计算loss时,G_loss 越小越好, G 网络生成的全是假数据,则x=D(G(z)), y=0,G_loss = BCELoss(x, 0) = -mean(log(1-D(G(z))))
对D网络计算loss时,D_Loss越大越好,而 \(x\in(0,1)\), 所以可以令 \(x_k=1-x\) 把越大越好问题 转化成 越小越好的问题。
输入分两种情况:
- D输入G生成的假数据时 x=D(G(z)),x1=1-D(G(z)), y1=0, D_loss_1 = BCELoss(x1, y1) = -mean(log(1-x1)) = -mean(log(D(G(z))))
- D输入真实数据时 x=D(k),x2=1-D(k), y2=1, D_loss_2 = BCELoss(x2, y2) = -mean(log(1-D(k)))
D的总损失 D_Loss = - mean(log(1-D(k)) + log(D(G(z)))) = BCELoss(1-D(G(z)), 0) + BCELoss(1-D(k), 1)
可以用 bceloss 进行替换
# G_loss = -torch.mean(torch.log(1.0 - D_fake + eps))
G_loss = bceloss(D_fake, torch.zeros_like(D_fake))
# D_loss = -torch.mean(torch.log(eps + 1.0 - D_real) + torch.log(eps + D_fake))
D_loss = bceloss(1-D_real, torch.ones_like(D_real)) + bceloss(1-D_fake, torch.zeros_like(D_fake))


