KMP算法实现及应用
1、KMP算法实现问题:
KMP算法实现就是字符查找问题,假设现在有这样一个问题,有一个文本串S和一个模式串P,要查找P在S中的位置,即从文本串S中找出模式串P第一次出现的位置。
问题分析:
假设文本串长度为n,模式串长度为m。
(1)暴力求解算法下,当两者匹配S[i] = P[j] 时,i++,j++;当不匹配时,i++,j=0。也就是说每次匹配失败时,模式串相对于文本串向右移动了一位。
时间复杂度为O(m*n),空间复杂度为O(1)。
(2)KMP算法下,当两者匹配S[i] = P[j] 时,i++,j++;当不匹配时,j = next[j](next[j] <= j-1)。也就是说每次匹配失败时,模式串相对于文本串向右至少移动一位,移动位数为j - next[j] >= 1。时间复杂度为O(m+n),空间复杂度为O(m)。
在实现KMP算法之前,必须获取模式串P的next数组,设next[j]=k,即模式串前j-1位有k前缀和k后缀相等。
获取模式串next数组程序实现:
1 void GetNext(char* p,int next[]){ 2 int plen = strlen(p); 3 int k = -1; 4 next[0] = -1; 5 int j; 6 //此时,k表示next[j-1],p[j]表示后缀,p[k]表示前缀 7 //k=-1表示未找到前缀后缀相等的情况,首次可先忽略 8 while(j < plen -1){ 9 if(k ==-1 || p[j] == p[k]){ 10 k++; 11 j++; 12 next[j] = k; 13 } 14 else{ 15 k = next[k]; 16 } 17 } 18 }
运行结果: 对于模式串 abaabcabc的next数组为:
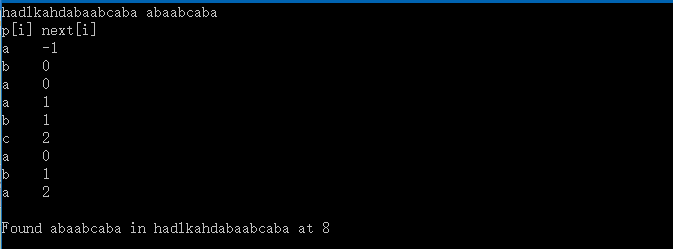
这里对next数组进行了改进,在原始的next数组中,当next[j] = k, p[j] = p[k]时,next[j] 可以直接等于next[k]。这样做的好处就是在KMP最差情况下,即模式串首字符与其他字符都相等的时候,时间复杂度能够提高,但还是在一个数量级。
改进next数组代码实现:
1 void GetNext1(char* p,int next[]){ 2 int plen = strlen(p); 3 int k = -1; 4 next[0] = -1; 5 int j; 6 //此时,k表示next[j-1],p[j]表示后缀,p[k]表示前缀 7 //k=-1表示未找到前缀后缀相等的情况,首次可先忽略 8 while(j < plen -1){ 9 if(k ==-1 || p[j] == p[k]){ 10 k++; 11 j++; 12 if(p[j] == p[k])//当前缀与后缀再次相等时,直接替换成next[k] 13 next[j] = next[k]; 14 else 15 next[j] = k; 16 } 17 else{ 18 k = next[k]; 19 } 20 } 21 }
运行结果:改进后next数组为:
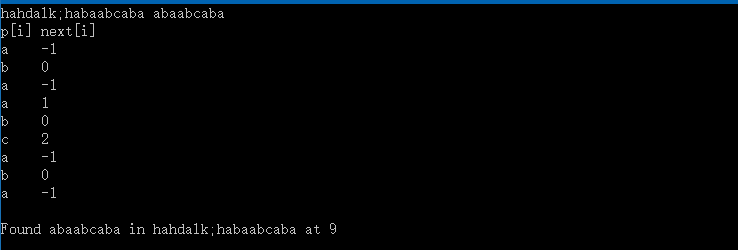
在获取模式串next数组后,就可以进行KMP算法,进行字符串的查找。
程序实现如下:
1 /*************************************** 2 FileName KMPCode.cpp 3 Author : godfrey 4 CreatedTime : 2016/5/8 5 ****************************************/ 6 #include <iostream> 7 #include <cstring> 8 #include <vector> 9 #include <algorithm> 10 #include <stdio.h> 11 #include <stdlib.h> 12 13 using namespace std; 14 15 void GetNext(char* p,int next[]){ 16 int plen = strlen(p); 17 int k = -1; 18 next[0] = -1; 19 int j; 20 //此时,k表示next[j-1],p[j]表示后缀,p[k]表示前缀 21 //k=-1表示未找到前缀后缀相等的情况,首次可先忽略 22 while(j < plen -1){ 23 if(k ==-1 || p[j] == p[k]){ 24 k++; 25 j++; 26 next[j] = k; 27 } 28 else{ 29 k = next[k]; 30 } 31 } 32 } 33 34 void GetNext1(char* p,int next[]){ 35 int plen = strlen(p); 36 int k = -1; 37 next[0] = -1; 38 int j; 39 //此时,k表示next[j-1],p[j]表示后缀,p[k]表示前缀 40 //k=-1表示未找到前缀后缀相等的情况,首次可先忽略 41 while(j < plen -1){ 42 if(k ==-1 || p[j] == p[k]){ 43 k++; 44 j++; 45 if(p[j] == p[k])//当前缀与后缀再次相等时,直接替换成next[k] 46 next[j] = next[k]; 47 else 48 next[j] = k; 49 } 50 else{ 51 k = next[k]; 52 } 53 } 54 } 55 56 int KMPCode(char* s,char* p,int p_next[]){ 57 int result = -1; 58 int plen = strlen(p); 59 int slen = strlen(s); 60 int i=0; 61 int j=0; 62 while(i < slen){ 63 if(j == -1 || s[i] == p[j]){ 64 i++; 65 j++; 66 } 67 else{ 68 j = p_next[j]; 69 } 70 71 if(j == plen){ 72 result = i - plen; 73 break; 74 } 75 } 76 return result; 77 } 78 int main() 79 { 80 char s[1024],p[1024]; 81 int next[1025]; 82 int num; 83 while(cin>>s>>p){ 84 //GetNext(p,next); 85 GetNext1(p,next); 86 int plen = strlen(p); 87 cout<<"p[i] "<<"next[i] "<<endl; 88 for(int i=0;i<plen;i++){ 89 cout<<p[i]<<" "<<next[i]<<endl; 90 } 91 cout<<endl; 92 num = KMPCode(s,p,next); 93 if(num == -1){ 94 cout<<"Not found "<< p <<" in " << s <<endl; 95 } 96 else{ 97 cout<< "Found " << p << " in " << s << " at " <<num<<endl; 98 } 99 } 100 return 0; 101 }
运行结果:

2、KMP算法应用问题
给定一个长度为n的字符串S,如果存在一个字符串P,重复若干次后P能够得到S,那么S叫做周期串,P叫做S的一个周期。
如:字符串abcabcabc为周期串,abc,abcabc是它的周期,其中abc是最小周期。设计算法,计算S的最小周期大小,如果不存在最小周期,返回-1。
问题分析:
计算S的next数组,这里求解的是原始的next数组。记last = next[n-1], p = n - 1 -last;如果n%p = 0,则p就是最小周期长度,前p个字符就是最小周期。自己可以画图理解一下,还是比较好理解的。
程序实现:
1 /*************************************** 2 FileName StringMinPeriod.cpp 3 Author : godfrey 4 CreatedTime : 2016/5/8 5 ****************************************/ 6 #include <iostream> 7 #include <cstring> 8 #include <vector> 9 #include <algorithm> 10 #include <stdio.h> 11 #include <stdlib.h> 12 13 using namespace std; 14 15 int StringMinPeriod(char* p){ 16 int plen = strlen(p); 17 if(plen == 0) 18 return -1; 19 int* next = new int[plen]; 20 int k = -1; 21 next[0] = -1; 22 int j = 0; 23 while(j < plen -1){ 24 if((k ==-1) || (p[j] == p[k])){ 25 k++; 26 j++; 27 next[j] = k; 28 } 29 else{ 30 k = next[k]; 31 } 32 } 33 34 next[0] = 0;//将首位恢复为逻辑上的零 35 int last = next[plen-1]; 36 if(last == 0) 37 return -1; 38 if(plen % (plen - last - 1) == 0) 39 return plen - last - 1; 40 delete[] next; 41 return -1; 42 } 43 44 int main() 45 { 46 char s[1024]; 47 int MinPeriod; 48 while(cin>>s){ 49 MinPeriod = StringMinPeriod(s); 50 cout<<"the string MinPeriod : " <<MinPeriod<<" "; 51 for(int i=0;i<MinPeriod;i++) 52 cout<<s[i]; 53 cout<<endl; 54 } 55 return 0; 56 }
运行结果:

转载请注明出处:
C++博客园:godfrey_88
posted on 2016-05-08 18:22 Brainer-Gao 阅读(629) 评论(0) 编辑 收藏 举报



