20182331 2019-2020-1《数据结构与面向对象程序设计》第10周学习总结

教材学习内容总结

无向图

1.图的概念（非线性结构）：允许树中每个结点与多个结点相连，不分父子结点。

2.图由顶点和边组成。

顶点由名字或标号来表示，如：A、B、C、D；
边由连接的定点对来表示，如：（A,B）,（C,D），表示两顶点之间有一条边。

3.无向图：顶点之间无序连接。
如：边（A,B）意味着A与B之间的连接是双向的，与（B,A）的含义一样。

4.邻接（邻居）：两个顶点之间有边连接。

5.自循环（悬挂）：自己连接到自己的边。

6.完全图：含有最多条边的无向图。例如：

无向图G是一个完全图。

7.路径：连接图中两个顶点的边的序列，可以由多条边组成。
<无向图中的路径是双向的。

8.路径长度：路径中所含边的数目（顶点个数减1）。

9.联通图：无向图中任意两个顶点间都有路径。例如：

完全图一定是连通图，连通图不一定是完全图。

10.环（回路）：第一个顶点与最后一个顶点相同且没有重复边的路径。例如：

11.无环图：没有环的图。

12.子图：类似集合中“子集”的概念，示例如下：

其中，（b），（c）是（a）的子图。

13.生成树：包含无向图G1所有顶点的极小连通子图称为G1的生成树。例如：

14.稀疏图与稠密图：有很少条边或弧（如e<nlogn，n是图的顶点数，e是弧数）的图称为稀疏图，反之称为稠密图。

有向图

1.有向图：顶点之间有序连接，边是顶点的有序对。

边（A,B）和（B,A）方向不同。

2.有向路径：连接两个顶点有向边的序列。

有向图中的有序对常用序偶表示，例如：

上图中路径 V0→V2→V3是从V0到V3的路径，但反过来不再成立。

注意联通有向图与无向图不同，有向边决定连通性。例如：

上图中左图为联通图，右图不联通，因为从任何顶点到顶点1都没有路径。

3.有向树是一个有向图，其中指定一个元素为根，则具有下列特性：

    任何顶点到根都没有连接。


    到达每个非根元素的连接都只有一个。


    从根到每个顶点都有路径。

顶点的度、出度、入度：

带权图

1.带权图（网络）：每条边都对应一个权值（数据信息）的图。（城市之间的航线、票价等）

带权图可以是无向的也可以是有向的。

2.带权图的边：由起始点、结束点和权构成。

有向图的每条边必须使用三元组表示。

常用的图算法

1.图的遍历：

2.广度优先遍历：从一个顶点开始，辐射状地优先遍历其周围较广的区域。

3.深度优先遍历：图的深度优先搜索，类似于树的先序遍历，所遵循的搜索策略是尽可能“深”地搜索图。

4.连通性：从任意结点开始的广度优先遍历中得到的顶点数等于图中所含顶点数。

生成树：包含图中所有顶点及图中部分边的一棵树。

5.最小生成树：所含边权值之和小于其他生成树的边的权值之和。

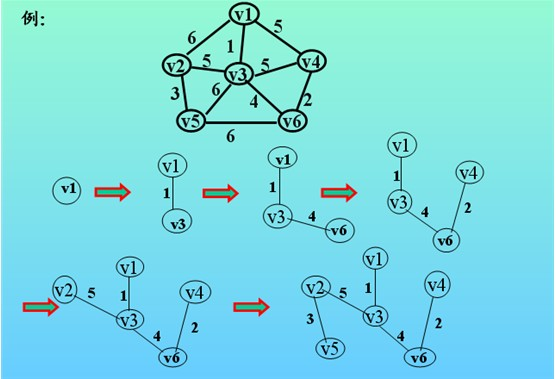
判定最短路径：

判定起始顶点和目标顶点之间是否存在最短路径（两个顶点之间边数最少的路径）。

在带权图中找到最短路径。（Dijkstra算法）
图的实现策略：

1.邻接矩阵：

2.无向图邻接矩阵：

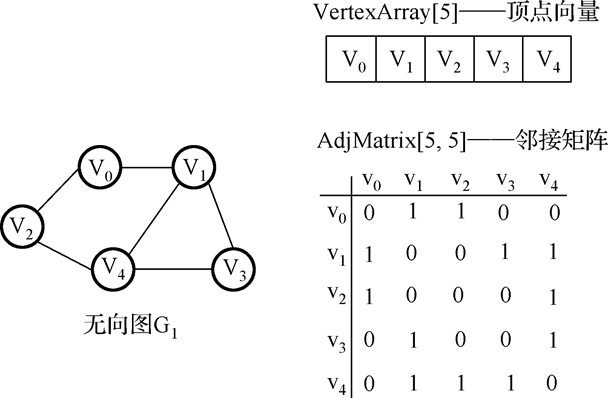
特点：对称，可压缩存储。顶点 vi 的度是邻接矩阵中第 i 行 1 的个数。

3.有向图邻接矩阵：

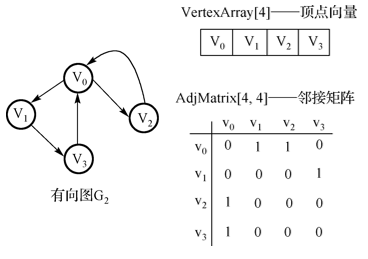
特点：不一定对称。顶点 vi 的出度是邻接矩阵中第 i 行 1 的个数。顶点 vi 的入度是邻接矩阵中第 i 列 1 的个数。

4.网的邻接矩阵：

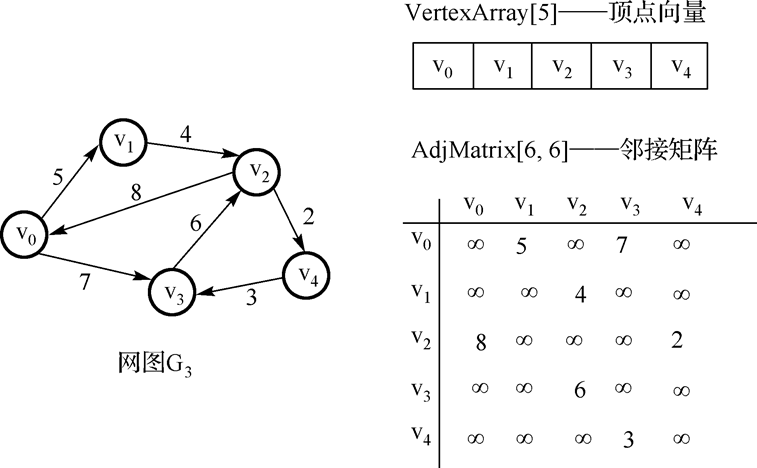
采用邻接矩阵表示图，优点：直观方便，运算简单。

时间复杂度：边查找O（1）；顶点度计算O（n）。
空间复杂度：O（n^2）（尽量不要用来表示稀疏图）。

5.边集数组：

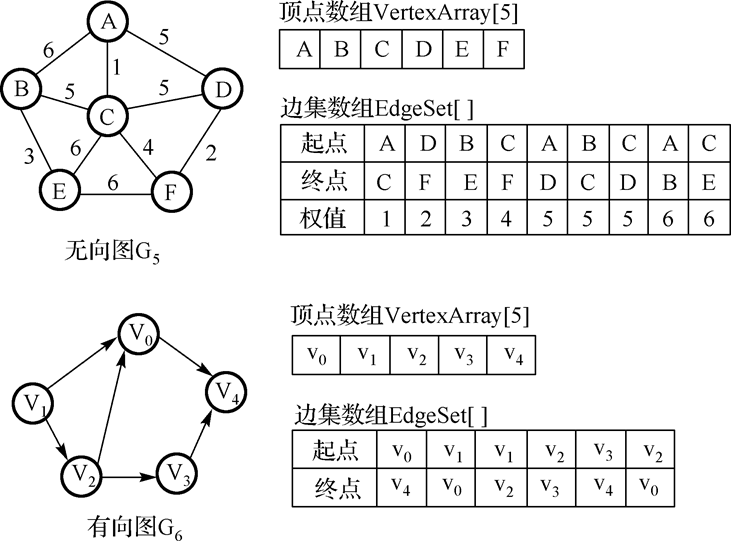
在边集数组中查找一条边或一个顶点的度都需要扫描整个数组，所以其时间复杂性为O（e）。

边集数组适合那些对边依次进行处理的运算，不适合对顶点的运算和对任一条边的运算。

边集数组表示通常包括一个 边集数组和一个顶点数组，所以其空间复杂性为O（n+e）。

从空间复杂性上讲， 边集数组也适合表示稀疏图。

6.无向图邻接表：

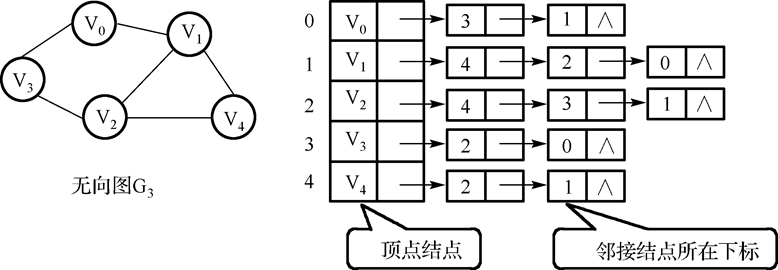
特点：若无向图中有 n 个顶点、e 条边，则其邻接表需 n 个头结点和 2e 个表结点。适宜存储稀疏图。
无向图中顶点 vi 的度为第 i 个单链表中的结点数。

7.有向图邻接表：

特点：顶点 vi 的出度为第 i 个单链表中的结点个数。
顶点 vi 的入度为整个单链表中邻接点域值是 i -1 的结点个数。
找出度易，找入度难。

8.逆邻接表：

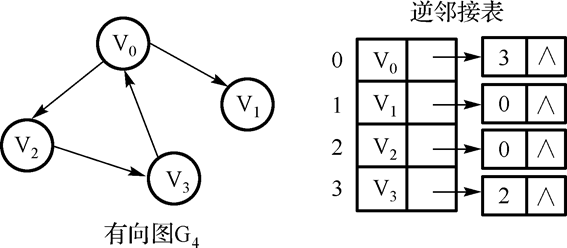
特点：顶点 vi 的入度为第 i 个单链表中的结点个数。
顶点 vi 的出度为整个单链表中邻接点域值是 i -1 的结点个数。
找入度易，找出度难。

9.带权邻接表：

邻接表用于表示稀疏图比较节省存储空间，因为只需要很少的边结点，若用于表示稠密图，则将占用较多的存储空间，同时也将增加顶点的查找结点时间。

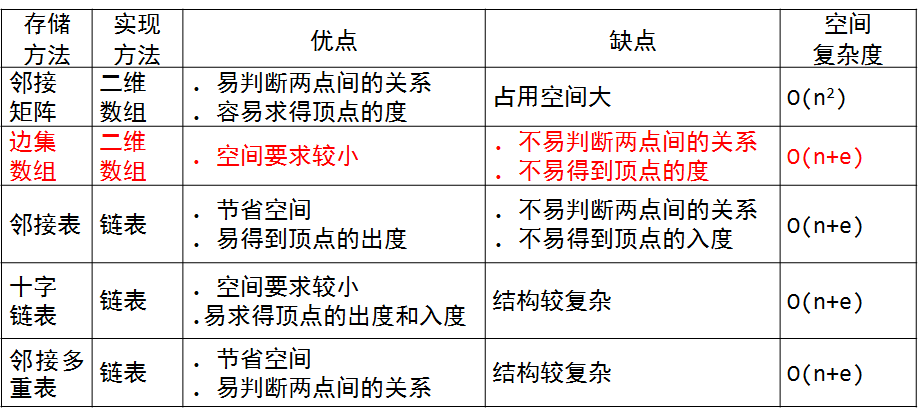
图的存储结构归结比较：

代码托管

教材学习中的问题和解决过程

问题1：广度优先遍历和深度优先遍历的实现过程
解决方案：

深度优先
深度优先遍历，从初始访问结点出发，我们知道初始访问结点可能有多个邻接结点，深度优先遍历的策略就是首先访问第一个邻接结点，然后再以这个被访问的邻接结点作为初始结点，访问它的第一个邻接结点。总结起来可以这样说：每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。

我们从这里可以看到，这样的访问策略是优先往纵向挖掘深入，而不是对一个结点的所有邻接结点进行横向访问。
具体算法表述如下：

1.访问初始结点v，并标记结点v为已访问。
2.查找结点v的第一个邻接结点w。
3.若w存在，则继续执行4，否则算法结束。
4.若w未被访问，对w进行深度优先遍历递归（即把w当做另一个v，然后进行步骤123）。
5.查找结点v的w邻接结点的下一个邻接结点，转到步骤3。

广度优先
类似于一个分层搜索的过程，广度优先遍历需要使用一个队列以保持访问过的结点的顺序，以便按这个顺序来访问这些结点的邻接结点。
具体算法表述如下：

1.访问初始结点v并标记结点v为已访问。
2.结点v入队列
3.当队列非空时，继续执行，否则算法结束。
4.出队列，取得队头结点u。
5.查找结点u的第一个邻接结点w。
6.若结点u的邻接结点w不存在，则转到步骤3；否则循环执行以下三个步骤：
```
  1). 若结点w尚未被访问，则访问结点w并标记为已访问。
  2). 结点w入队列
  3). 查找结点u的继w邻接结点后的下一个邻接结点w，转到步骤6。
```

代码调试过程中的问题和解决过程

问题1：在实现邻接矩阵的时候，遇到不清楚如何表示横纵两种数据，两个牌子，一套数据，知道应该用二维数组，但是实现起来还是遇到了困难，不知道该如何实现？
问题1解决方案：代码如下：


    public class asd {
    public static void main(String[] args) {
    int a[] = {0,1,2,3,4};
    int b[][] = new int[5][5];
    int i=0,j,count = 0;
    Scanner in = new Scanner(System.in);
    System.out.println("V(" + i + "):");
    for(i = 0;i < 5;i++){
        for(j = 0 ;j < 5 ; j++){
           b[i][j] = in.nextInt();
        }
        if(i < 4)
        {
            System.out.println("V(" + (i+1) + "): ");
        }
    }

    for(i = 0;i < 5;i++){
        System.out.print("V(" + i + "):   ");
        for(j = 0 ;j < 5 ; j++){
            System.out.print( b[i][j] + "  " );;
        }
        System.out.println();
    }

    for(i = 0;i < 5;i++){
        count   = 0;
        System.out.print("V(" + i + ")的出度为：  ");
        for(j = 0 ;j < 5 ; j++){
            if(b[i][j] != 0){
                count++;
            }

            //System.out.print( b[i][j] + "  " );;
        }
        System.out.println(count);
    }
    System.out.println();
    System.out.println();
    for(i = 0;i < 5;i++){
        count   = 0;
        System.out.print("V(" + i + ")的入度为：  ");
        for(j = 0 ;j < 5 ; j++){
            if(b[j][i] != 0){
                count++;
            }

            //System.out.print( b[i][j] + "  " );;
        }
        System.out.println(count);
    }

结对及互评

博客中值得学习的或问题：
- 学习深刻，自己有方法
- 代码中值得学习的或问题：
- 使用继承减少代码的重复编写
- 基于评分标准，我给本博客打分：8分。得分情况如下：
- 正确使用Markdown语法（加1分）
- 模板中的要素齐全（加1分）
- 教材学习中的问题和解决过程, 一个问题加1分
- 代码调试中的问题和解决过程, 一个问题加1分
- 有动手写新代码的加1分
- 结对学习情况真实可信的加1分

点评过的同学博客和代码

本周结对学习情况
20182309
- 结对学习内容
  -自学教材第19章
- 代码托管到码云上
- 完成课后自测题，并参考答案学习
- 完成课后练习题
- 完成程序设计项目，至少完成pp19.1，pp19.3

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）
目标	5000行	30篇	400小时
第一周	109/109	2/2	20/20
第二、三周	729/838	2/4	47/67
第四周	750/1588	2/6	22/89
第五周	1588/2698	2/7	34/133
第六周	1350/4035	2/9	24/157
第九周	3364/7399	5/14	97/254
第十周	618 /8071	1/15	22/276
第十一周	742 /8843	3/18	16/292
第十二、十三周	2815/11658	2/20	35/321

posted @ 2019-11-30 21:11 20182331 阅读(279) 评论(0) 编辑收藏举报

刷新页面返回顶部

20182331