leetcode刷题笔记五 最长回文子串 Scala版本

leetcode刷题笔记五 最长回文子串 Scala版本

源地址： leetcode刷题笔记五 最长回文子串 Scala版本

问题描述

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Example 2:

Input: "cbbd"
Output: "bb"

简要思路分析：

1.暴力法 针对以S串中任一字符开头的满足所有要求的子串进行判断，时间复杂度为O(n^3).

object Solution {
 def longestPalindrome(s: String):String = {
   var length = 0
   var maxLength = 0
   var start = 0

   if (s.isEmpty) return ""

   if (s.length == 1) return s
   
   //if (s.length == 2 && s == s.reverse) return s 

   for (i <- 0 until s.length) {
     for (j <- i+1 to s.length) {
       if (s.substring(i, j) == s.substring(i, j).reverse) {
         length = j - i
       }
       if (length > maxLength) {
         maxLength = length
         start = i
       }
     }
   }
     return s.substring(start, start + maxLength)
 }
}

2.动态规划

根据分析，构建状态转换方程。
$$
dp[i,j] = \begin{cases} 0 , \text{if } s(i) \text{ != } s(j) \ dp[i+1,j-1] , \text{if } s(i) \text{ = } s(j)\end{cases}
$$
具体情况如下：

(i) 空串 ， 直接返回空串

(ii) 初始化。

对于所有dp[i,i]置1，即所有单个字符可以被视为长度为1的子串。

对对角线内测数据进行判断，即对满足条件的dp[i,i+1]置1，否则置0

(iii) 按照状态转换方程，对于dp中剩余的位置中回文串置1.注意边缘条件

串	a	b	a	b	a
A	1
B	0	1
A	1	0	1
B	0	1	0	1
A	1	0	1	0	1

object Solution {
    def longestPalindrome(s: String): String = {
         var length = 0
   var maxLength = 1
   var start = 0
   var dp = Array.ofDim[Boolean](s.length,s.length)

   if(s == "") return ""

   //init dp Array
   for (i <- 0 until s.length-1){
     dp(i)(i) = true
     if(s(i) == s(i+1)){
       dp(i)(i+1) = true
       //println(i)
       start = i
       maxLength = 2
     }
     else{
       dp(i)(i+1) = false
     }
   }
   dp(s.length-1)(s.length-1) = true
   //dp.foreach(x => for (elem <- x) print ((elem).toString))

   for {
     k <- 2 to s.length
     i <- 0 to s.length - 3
     j = Math.min(i + k, s.length - 1)
   } {
       if (s(i) == s(j) && dp(i+1)(j-1) == true){
         dp(i)(j) = true
         //println("i: " + i.toString + " j: " + j.toString)
       }
       else dp(i)(j) = false
       length = j -i + 1
       if(dp(i)(j) == true && length > maxLength){
         maxLength = length
         start = i
       }

   }
   return s.substring(start,start+maxLength)
 }
}

注：这里使用boolean型二维数组，使用int型数组会超出内存需求。时间复杂度为O(n^2)级

3.Manachar算法

Manachar算法主要用于回文处理

Manachar算法准备部分 -- 将奇偶串变为奇数串(去除对称轴不确定性)

数学原理： 奇 + 偶 = 奇

具体做法：对字符串的首部、尾部和间隙加入相同的标记字符

i	1	2	3	4	5	6	7	8	9	10	11
原串	a	b	c	b	a
初始化串	#	a	#	b	#	c	#	b	#	a	#
P[i]	1	2	1	2	1	6	1	2	1	2	1
P[i]-1,回文串长度	0	1	0	1	0	5	0	1	0	1	0

i	1	2	3	4	5	6	7	8	9	10	11	12	13
原串	a	b	c	c	b	a
初始化串	#	a	#	b	#	c	#	c	#	b	#	a	#
P[i]	1	2	1	2	1	2	7	2	1	2	1	2	1
P[i]-1,回文串长度	0	1	0	1	0	5	0	1	0	1	0	1	0

Manachar 算法

假设 i 为当前字符所在改造后字符串的位置，P[i]为i位置对应的P值， pos为目前已访问的最大回文子串的中心位置，mx为pos+P[pos] （当前已访问最大回文子串的右端）

这里算法描述参考知乎 上牛客竞赛的说明：https://zhuanlan.zhihu.com/p/67171603

具体情况主要分为两大类：

1. i < mx

   对于i < mx的情况，主要通过回文对称机制处理。就这种情况下，可以继续细分为3种。

   （1）

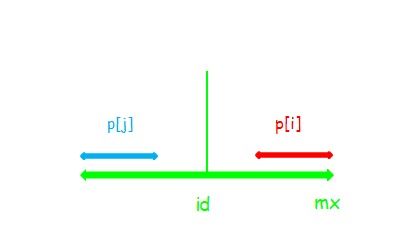
由图易知，显然此时 p[i] = p[j] 。

对于这种情况，串 i不可以再向两边扩张。

如果可以向两边扩张的话， p[j]也可以再向两边扩张，而 p[j]已经确定了，所以串 i不向两边扩张。

(2)

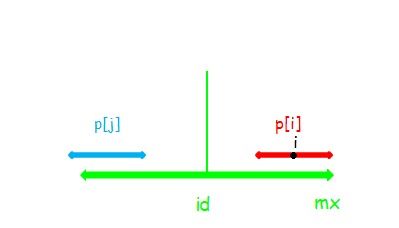
由图易知，此时p[i] = p[j] 。对于这种情况，串 i可以再向两边扩张。

​ （3）

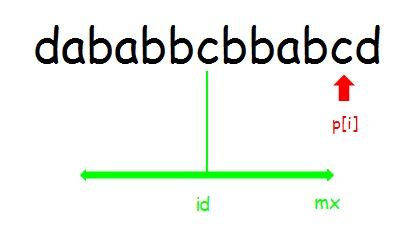
显然p[j]可以再拓展，但是由于已经抵达边界，不能有效的展开p[j]，从而p[i]的值不能直接使用p[j]的值，这是我们只能确定串i在m以内的部分是回文的，并不能确定串i和串j相同。所以我们认为串i的回文长度至少为mx-i.

综上，当i<mx时，p[i] = min(p[2*pos-i], mx-i)

2.i >= mx

这时 i已经跳出回文串后端mx。不能通过回文性质计算P[i]。我们需要将p[i]设为1.

结合以上两种情况，我们对p[i]的计算将采取以下方法：

//对 i<mx情况进行处理
(i < mx) match{
           case true => arrP(i) = math.min(arrP(2*pos-i), mx-i)
           //对i >= mx进行处理
           case _ => arrP(i) = 1
         }
		 //尝试对i暴力拓展
         while (sS(i-arrP(i)) == sS(i+arrP(i))) arrP(i)+=1
		//对mx，pos进行更新
         if (arrP(i)+i > mx) {
           mx = arrP(i) + i
           pos = i
         }

具体代码如下：

object Solution {
    def longestPalindrome(s: String): String = {

   //
   var start = 0
   var length = 0
   var pos = 0
   var mx = 0


   if (s == "" || s.length == 1)  s

   var sS = "^#"
   s.foreach(x => sS += x + "#")
   sS += "$"
   println(sS.length)


   var arrP = Array.ofDim[Int](sS.length)
   println(arrP.length)

   for(i <- 1 until sS.length-1 ){
      //arrP(i) = if (i < mx) math.min(arrP(2*pos-i), mx-i) else 1
     (i < mx) match{
        case true => arrP(i) = math.min(arrP(2*pos-i), mx-i)
        case _ => arrP(i) = 1
      }

      while (sS(i-arrP(i)) == sS(i+arrP(i))) arrP(i)+=1
      if (arrP(i)+i > mx) {
        mx = arrP(i) + i
        pos = i
      }
     //println("----------------------------")
     //println("i :" + i.toString)
     //println("arrP(i) :" + arrP(i).toString)
     //println("mx: " + mx.toString)
     //println("pos: "+pos.toString)

     if (arrP(i)-1 > length){
       length = arrP(i)-1
       start = (i - arrP(i))/2
     }
   }

   //arrP.slice(1,s.length-1).foreach(x => if (x > length) {length = x})
   //arrP.slice(0,sS.length).foreach(x => println(x))
   //return (length-1).toString
   return(s.substring(start,start+length))
 }
}

import "fmt"
func longestPalindrome(s string) string {
    slen := len(s)
    str := "#"
    for i:=0; i < slen; i++ {
        str += string(s[i]) + "#"
    }
    
    strLen := len(str)
    arr := make([]int, strLen)
    start, maxLen, maxRight, center := 0, 0, 1, 0

    for i := 0; i < strLen; i++ {
        if i < maxRight {
            mirror := 2 * center - i
            arr[i] = min(arr[mirror], maxRight - i)
        } 
        
        for left, right := i - (1 + arr[i]), i + (1 + arr[i]); left >= 0 && right < strLen && str[left] == str[right]; left, right = left-1, right+1 {
            arr[i] += 1
        }

        if i + arr[i] > maxRight {
            maxRight = i + arr[i]
            center = i
        }

        if arr[i] > maxLen {
            maxLen = arr[i]
            start = (i -maxLen)/2
        } 
    }

    return s[start: start+maxLen] 
}

func min(a int, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}