第四次实验报告

c语言程序报告

姓名：韦小闻     实验地点：第一教学楼514教室     实验时间：4月30日

一、实验目的与要求

1.编写由三角形三边求面积的函数

• 调用area()函数求三角形的面积
• 在求面积函数运用海伦公式

2.编写求N阶乘的函数

• 定义符号常量
• 使用长整型变量存放累乘积
• 使用全局变量存放累乘积

3.求两个整数的最大公约数

• 调用bcd()函数求两个整数的最大公约数
• 掌握辗转相除法求两个整数的最大公约数

4.打印输出指定图形

• 调用trangle()函数输出三角形
• 在trangle()函数中用for循环的嵌套输出指定的结果

5.模块化程序设计

• 编制一个函数facsum(m),返回给定正整数m的所有因子(包括1但不包括自身)之和
• 编制一个主函数，调用(1)中的函数facsum(),寻找并输出500以内的所有亲密数对
• 输出要有文字说明。在输出每对亲密数时，要求从小到大排列并去掉重复的亲密数对
• 所有函数中的循环均为for循环

二、实验内容

6.4.1.1.编写由三角形三边求面积的函数

1.问题的描述：编写程序，从键盘输入三角形的3条边，调用三角形面积函数求出其面积，并输出结果。

2.程序流程图：

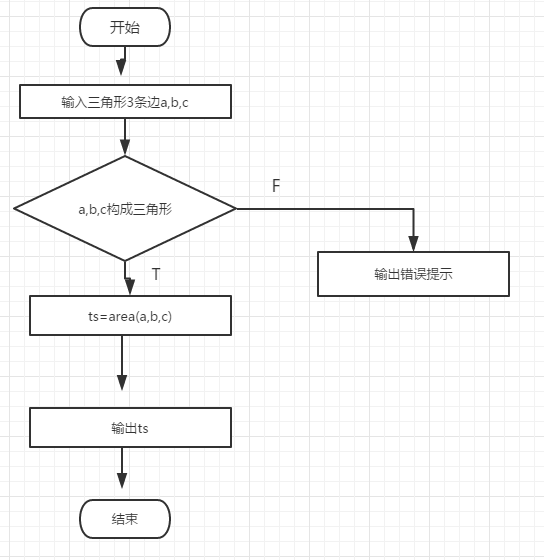
3.程序代码：

#include<math.h>
#include<stdio.h>
float area(float a,float b,float c)
{
 float s,p,area;
 s=(a+b+c)/2;
 p=s*(s-a)*(s-b)*(s-c);
 area=sqrt(p);
 return(area);
}
main()
{
 float x,y,z,ts;
 scanf("%f,%f,%f",&x,&y,&z);
 ts=area(x,y,z);
 if(x*x+y*y>=z*z&&y*y+z*z>=x*x&&x*x+z*z>=y*y)
 printf("area=%f\n",ts);
 else printf("data error!");
}

 

4.运行结果：主要难点就是三角形的面积算法，其次就是判断三角形的算法，最后函数调用，问题不大。

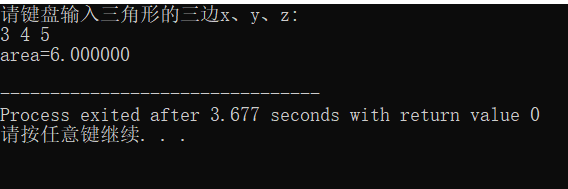
5.问题分析：

6.4.1.2、编写求N阶乘的函数

1.问题的描述：编写函数，求出从主函数传来的数值i阶乘值，然后将其传回主调函数并输出。

2.流程图：

3.实验代码：

4.运行结果：

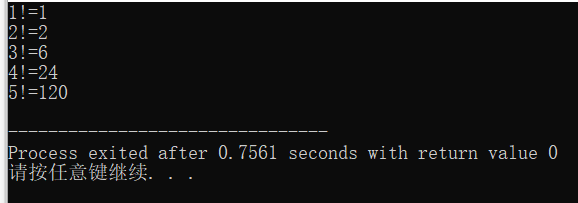
5.问题分析：主要就是如何定义局部静态变量，然后就是把求得的阶乘值保存在局部静态变量中，最后就是调用函数，难点就是这些，其他的没什么大问题。

6.4.1.3、求两个整数的最大公约数

1.问题的描述：编写程序，从键盘输入两个整数，调用gcd()函数求他们的最大公约数，并输出结果。

2.流程图：

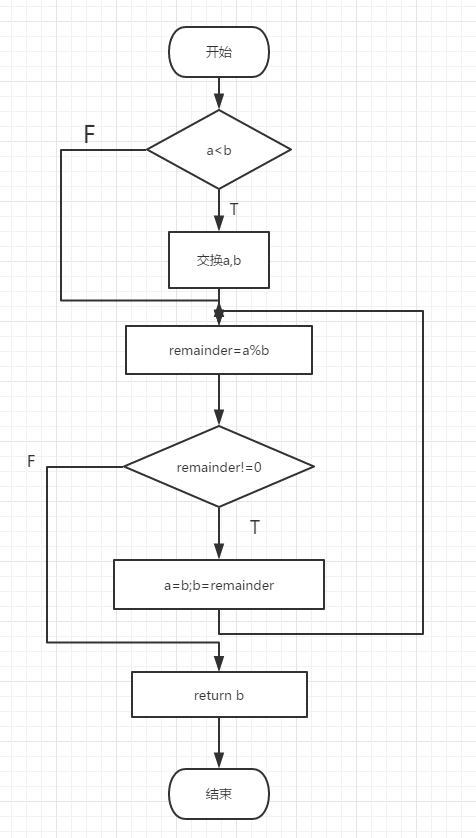
3.实验代码：

#include<stdio.h>
int gcd(int a,int b)
{
 int temp;
 int remainder;
 if(a<b)
 {
  temp=a;a=b;b=temp;/*交换a和b的值*/
 } 
 remainder=a%b;
 while(remainder!=0)
 {
  a=b;b=remainder;/*辗转相除求最大公约数*/
  break;
 }
 return b;
}
main()
{
 int x,y;
 int fac;
 printf("please input two integers:");/*提示输入两个整数*/
 scanf("%d,%d",&x,&y);/*输入两个数字*/
 fac=gcd(x,y);/*用输入的两个数调用求最大公约数的函数*/
 printf("The great common divisor is:%d",fac);
}

4.运行结果：

5.问题分析：这题难度较大，求最大公约数时需用的辗转相除法，这个我们是不知道的，后来老师讲了我就会用了。

6.4.1.4、打印输出指定图形

1.问题的描述：输入整数n，输出高度为n的等边三角形，当n的值为5，等边三角形为：

    *

   ***

  *****

 *******

**********

 

2.实验代码：

#include<stdio.h>
void trangle(int n)
{
 int i,j,k;
 for(i=0;i<=n;i++)
 {
  for(j=1;j<=(n-i);j++)
  printf(" ");/*打印每一行的空格*/ 
  for(k=1;k<=(2*i-1);k++)
  printf("*");/*打印每一行的*号*/ 
  putchar('\n');
  
 } 
}
main()
{
 int n;
 printf("please input one integers n:"); 
 scanf("%d",&n);
 printf("\n");
 trangle(n);/*调用函数打印出等边三角形*/ 
}

3.运行结果：

4.问题分析：这题之前遇到过，有一次实验报告就是写这个的，问题不大。

6.4..2.1模块化程序设计

1,问题描述：若正整数A的所有因子（包括1但不包括自身，下同）之和为B，而B的因子之和为A，则称A和B为一对亲密数。例如，6的因子之和为1+2+3=6，因此6与6为一对亲密数（即6自身构成一对亲密数）；又如，220的因子之和为1+2+4+5+10+11+20+22+44+55+110=284，而284的因子之和为1+2+4+71+142=220，因此，220与284为一对亲密数。
求500以内的所有的亲密数对。

2,流程图：

 

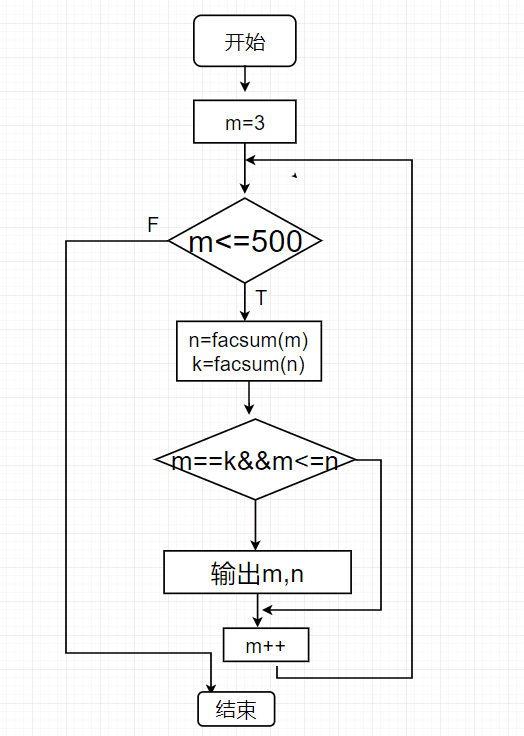
3.实验代码：

#include<stdio.h>
int facsum(int m)
{
 int  sum=1,f;
 for(f=2;f<=m/2;f++)/*for循环的循环体*/ 
 {
  if(m%f==0)
  sum=sum+f;
 }
 return sum;
} 
main()
{
 int m,n,k;
 for(m=3;m<=500;m++)/*求500以内亲密数对的for循环体*/ 
 {
  n=facsum(m);/*调用facsum求m的因子之和并存入k中*/ 
  k=facsum(n);/*调用facsum求k的因子之和*/ 
  if(m==k&&m<=n)/*判断是否是亲密数对的if条件语句*/ 
  printf("输出亲密对：%d,%d\n",m,n);
 }
}

4.运行结果：

5.问题分析：这题计算亲密对数的算法难度较大，还是参考流程图做的，如果没有提供流程图，是不会做的。

三、实验小结：

本次实验课任务量比较重，我们只做了5道题，这五道题对于我们来说还是有挑战性的，毕竟随随便便是做不出来，那些算法和细节太重要了。