[转]背包问题的贪心求解
题目
有一个背包,背包容量是M=150。有7个物品,物品可以分割成任意大小。
要求尽可能让装入背包中的物品总价值最大,但不能超过总容量。

思路
具有最优子结构性质和贪心选择性质。只要是所有物品的总重量大于背包容纳量,那么背包一定能装满。注意背包问题与0-1背包问题的区别。
这2类问题都具有最优子结构性质,极为相似,但背包问题可以用贪心算法求解,而0-1背包问题却不能用贪心算法求解。
算法逻辑
用贪心算法解背包问题的基本步骤:首先计算每种物品单位重量的价值v[i]/w[i],然后,依贪心选择策略,将尽可能多的单位重量价值最高的物品装入背包。若将这种物品全部装入背包后,背包内的物品总重量未超过C,则选择单位重量价值次高的物品并尽可能多地装入背包。依此策略一直地进行下去,直到背包装满为止。
代码实现
#include <iostream>
using namespace std;
//按照单位重量的价值量大小降序排列
void Sort(int n,float *w,float *v)
{
int i,j;
float temp1,temp2;
for(i=1;i<=n;i++)
for(j=1;j<=n-i;j++)//冒泡排序
{
temp1=v[j]/w[j];
temp2=v[j+1]/w[j+1];
if(temp1<temp2)
{
swap(w[j],w[j+1]);
swap(v[j],v[j+1]);
}
}
}
int main()
{
float w[101];//用来表示每个物品的重量
float v[101];//用来表示每个物品的价值量
float x[101];//表示最后放入背包的比例
int n;//物品数
float M;//背包最大容纳重量
cin>>n>>M;
//依次输入每件物品的重量和价值量
for(int i=1;i<=n;i++)
cin>>w[i]>>v[i];
//按照单位重量的价值量大小降序排列
Sort(n,w,v);
int i;
for(i=1;i<=n;i++)
x[i]=0;//初始值,未装入背包,x[i]=0
float c=M;//更新背包容纳量
for(i=1;i<=n;i++)
{
if(c<w[i]) break;//不能完全装下
x[i]=1;
c=c-w[i];
}
if(i<=n)
x[i]=c/w[i];
//输出
for(int i=1;i<=n;i++)
cout<<"重量为"<<w[i]<<"价值量为"<<v[i]<<"的物品"<<"放入的比例为"<<x[i]<<endl;
return 0;
}
最终结果
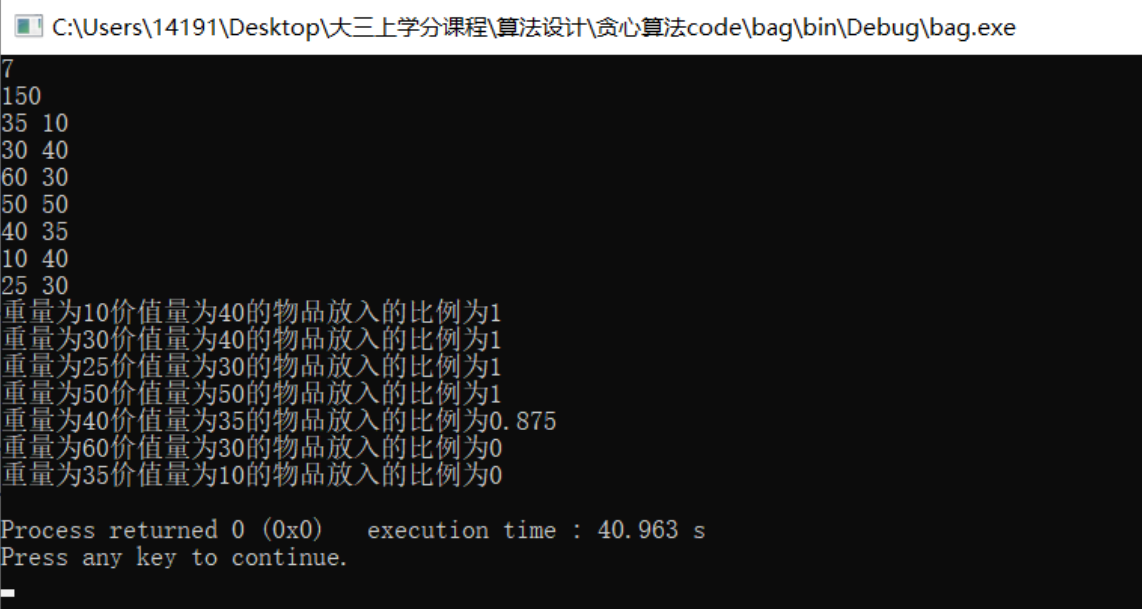
背包问题的贪心策略常见的有三种:
1.优先选择价值高的物品,这样可以保证装入背包的价值有效增长,但背包容量消耗过快。
2.优先选择重量小的物品,可以保证背包中装入尽可能多的物品,但物品的价值却不能保证有效增长。
3.结合物品的价值与重量,选择一个新的权重=价值/重量来衡量物品,优先装入权重大的,这样不仅能保证价值的有效增长,还能解决背包容量消耗过快的问题。
