一个动态规划的简单例题
动态规划(Dynamic Programming)
它是计算机中解决最优化问题的一种方法,效率高,速度快。
一般思路:
- 1、穷举法/暴力搜索
- 2、记忆化搜索/剪枝
- 3、改写成迭代形式
思想#
1.动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题
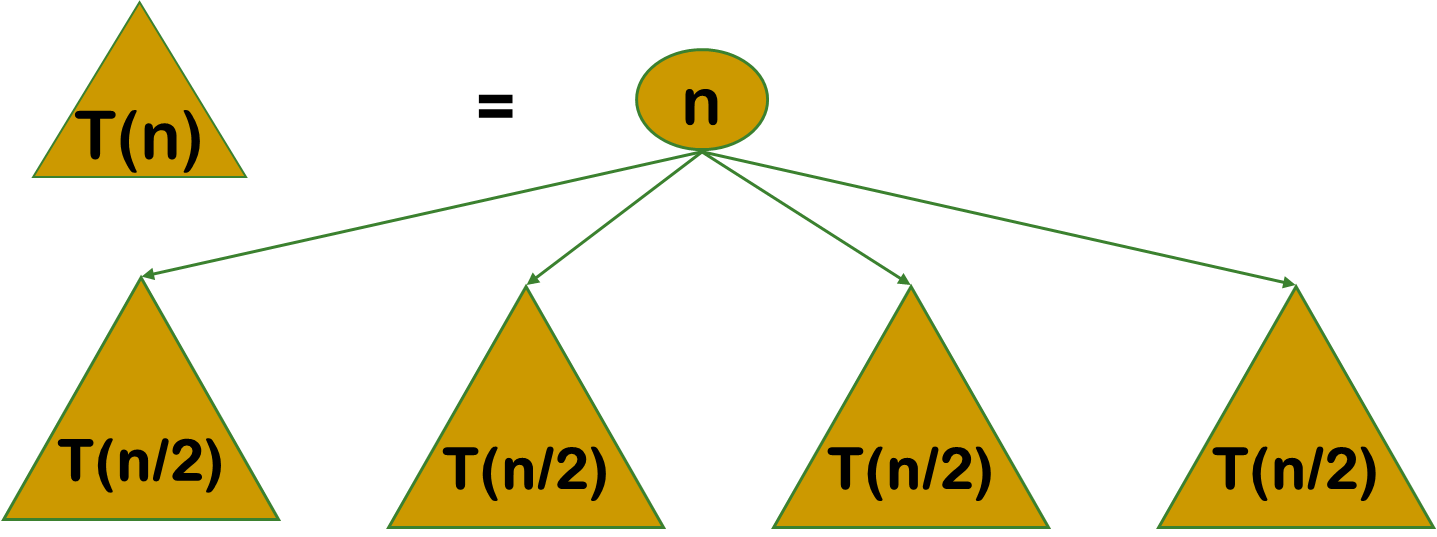
2.但是经分解得到的子问题往往不是互相独立的。不同子问题的数目常常只有多项式量级。在用分治法求解时,有些子问题被重复计算了许多次。
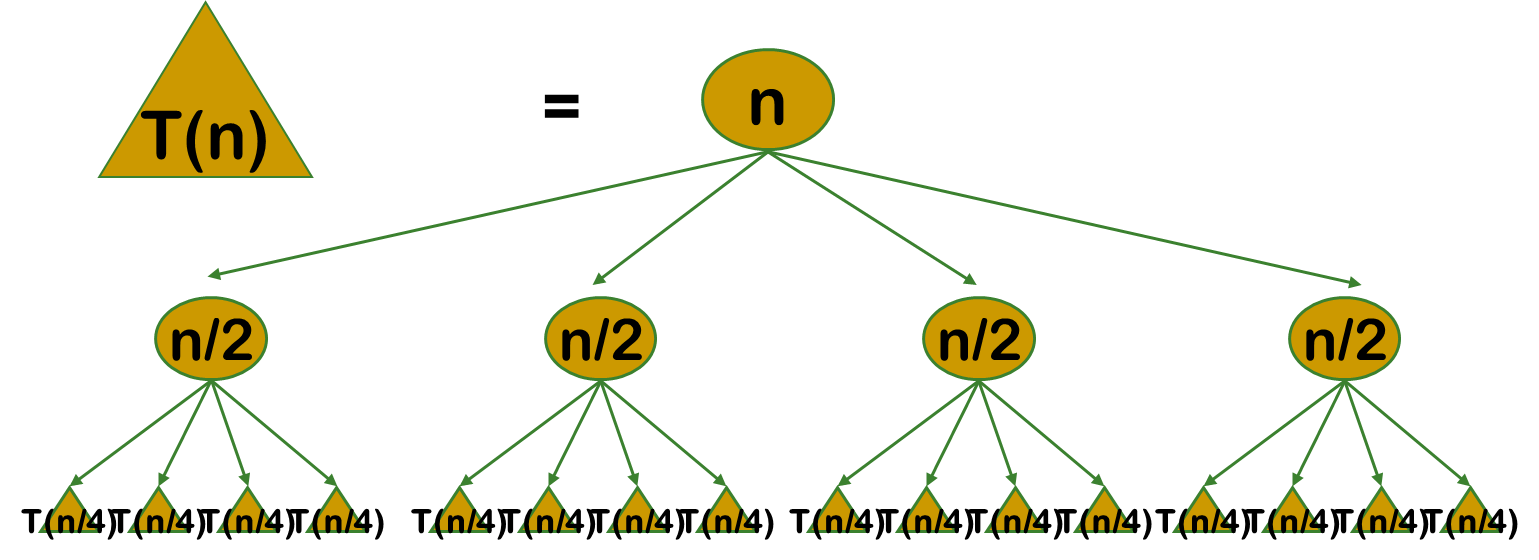
3.如果能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,就可以避免大量重复计算,从而得到多项式时间算法。
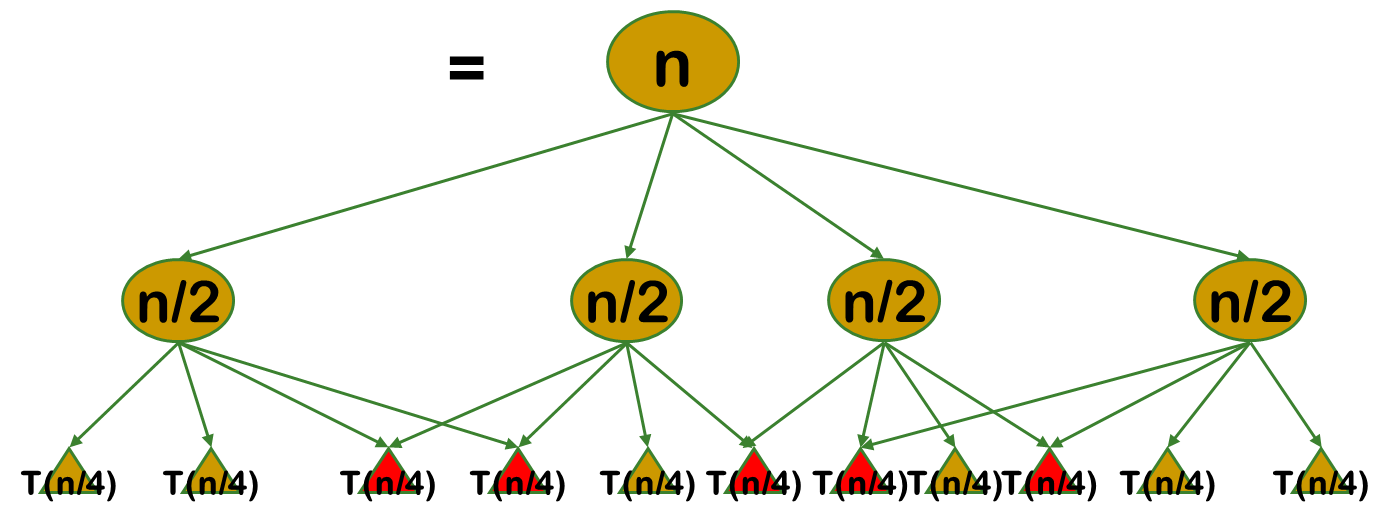
例题
e.g#
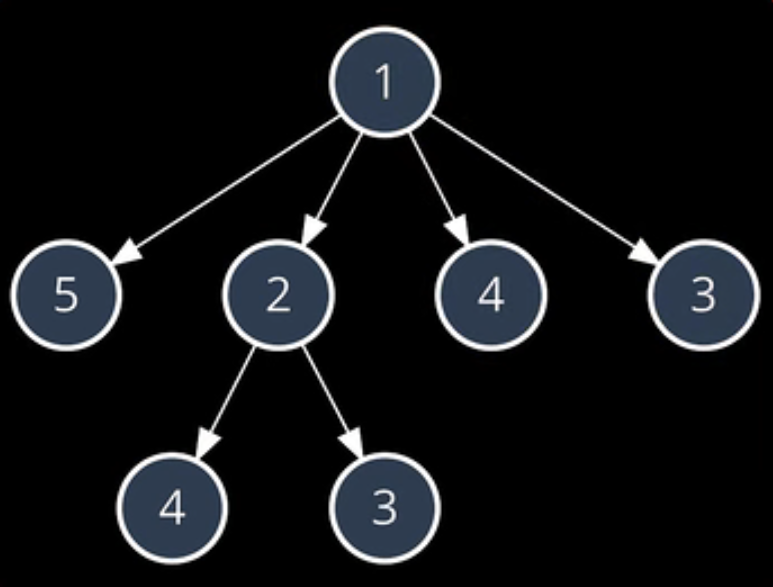
找出最长的递增的子序列 ,nums = [1,5,2,4,3]
给了一个无序的数组,要求我们找出其中最长的递增的子序列,比如:1,2,4就是其中的一个;1,2,3是另外一个。
我们可以将问题简化:要求这个算法只返回最长序列的“长度”
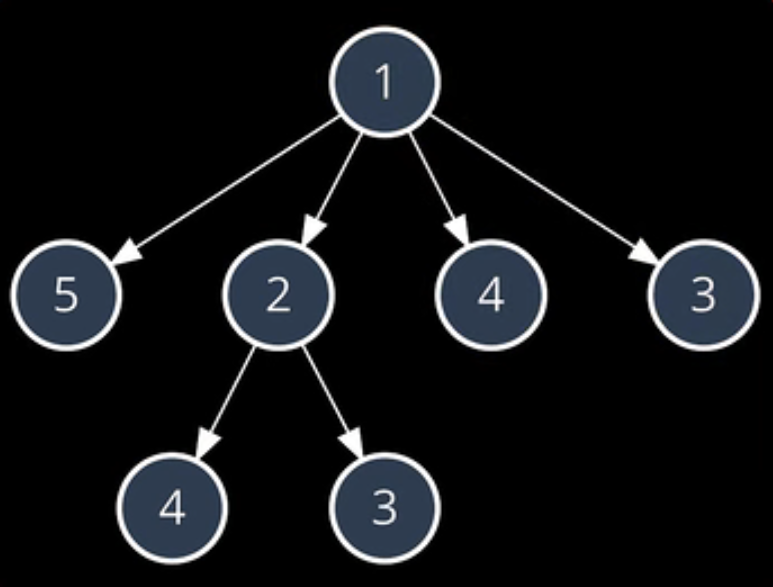
利用暴力枚举/暴力搜索:从“1”出发,最长递增子序列长度:3
算法实现:
def L( nums , i ):# 我们可以定义一个函数L,这个函数会返回从数组第i个数字开始的最长子序列长度
if i == len(nums) - 1 : # 取到最后一个数字
return 1
for j in range ( i + 1 ,len( nums ) ) : # 检查i后面的所有数字,将索引记为j
#遍历所有的j
if nums [ j ] > nums [ i ] : # 只要这个数比当前数大(也就是说可以构成递增序列)
max_len = max( max_len , L( nums , j ) + 1) # 递归的调用函数自身,去计算从j开始的最长子序列长度,然后+1得到目前这个序列的总长度
return max_len
# 接下来只需要对数组中的每一个数i ,依次调用L函数,然后选出长度最长的那个返回即可
def length_of_LTS(nums):
return max(
L(nums , i )for i in range ( len( nums))
)
# 可以带入之前的数据进行测试
nums = [1,5,2,4,3]
print(length_of_LTS(nums))
算法优化:记忆化搜索#
再次观察下方的遍历树,我们遍历子序列1,2,4的时候就已经计算过"从4开始的最大子序列的长度",后面遍历1,4的时候又计算了一次。因此算法存在大量重复的计算。
解决方案的关键是我们可以在第一次计算的时候,将结果保留下来。
def L( nums , i ):
if i in memo:# 看开头是否保存过这个答案
return memo [ i ]# 如果是,直接返回结果
# 否则再去计算答案
if i == len(nums) - 1: # 取到最后一个数字
return 1
for j in range ( i + 1 ,len( nums ) ) :
if nums [ j ] > nums [ i ]:
max_len = max( max_len , L( nums , j ) + 1) # 遍历所有的j
memo[ i ] = max_len # 哈希表,记录下“从i开始最长的子序列长度”
return max_len
def length_of_LTS(nums):
return max(
L(nums , i )for i in range ( len( nums))
)
这里用到了记忆化搜索,这也就是为什么大家常说用空间换时间
迭代/非递归的实现#
从最后的式子可以推至开头的式子,是不是很像数学归纳法?
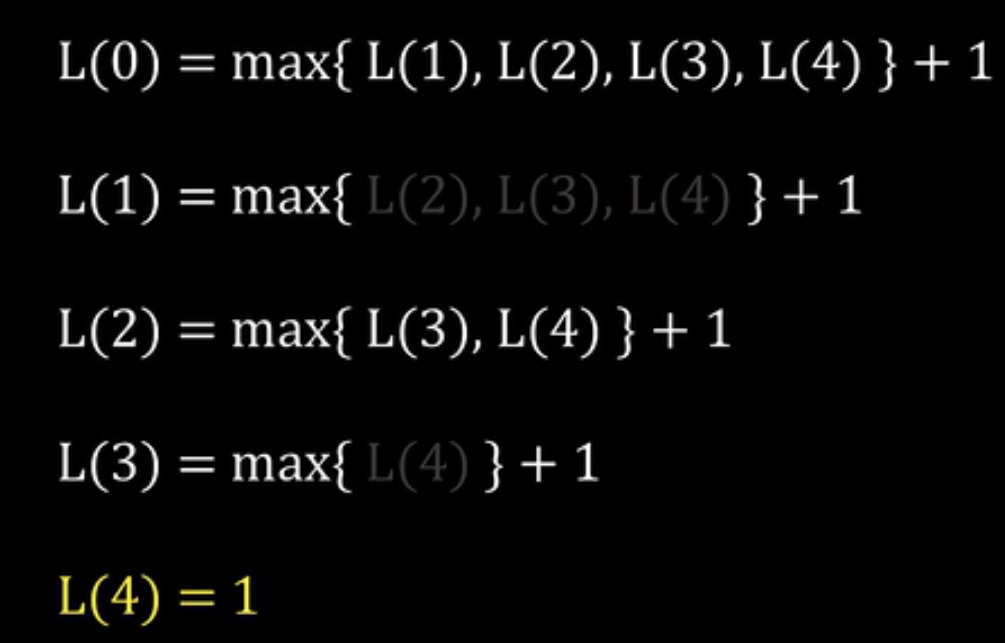
def length_of_LTS(nums);
n = len( nums ) # 5
L = [1 ] * n # initial value: [1,1,1,1,1]
# 通过两个循环,外面的循环代表从下往上的依次计算;里面的循环用于遍历括号中的这些数值,运算的结果可以存放到一个数组中,直接叫L
for i in reversed(range(n)): # i -> 4,3,2,1,0
for j in range(i + 1 , n):
if nums [ j ] > nums [ i ] :
L[ i ] = max(L[ i ],L [ j ] + 1)
return max(L)
10分钟彻底搞懂“动态规划”算法_哔哩哔哩_bilibili
配套视频的链接哦




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通