二分检索法
1.递归的基本思想
(1)何为递归?
递归顾名思义就是´递´和´归´
所谓的‘递’也就是“向下递去”,这个问题可以分解为若干个且形式相同的子问题,这些子问题可以使用相同的思路来解决。
所谓的‘归’也就是“归来的意思”,什么时候归来?所以涉及到了临界点,也就是‘递’中的分解终止条件。
递归的工作原理?
根据以上分析可以发现这个流程和栈的工作原理一致,递归调用就是通过栈这种数据结构完成的。整个过程实际上就是一个栈的入栈和出栈问题。然而我们并不需要关心这个栈的实现,这个过程是由系统来完成的。
递归的惯性解题思路
递归本质上类似数学中的归纳法,但又有所不同。(递归是从F(n)倒推到F(1),然后在F(1)回溯到F(n);相比于归纳法多了一步。)
void func(mode) {
if (endCondition) //临界条件
{
constExpression //处理方法
} else {
accumrateExpreesion //归纳项
mode = expression //步进表达式
func(mode) //调用本身,递归
}
}
递归的三要素
1、缩小问题规模
这个缩小问题规模可以根据归纳法先进行回推,比如让求S(n),我们可以先求当n=1的解决方法,再求n=2时的解决方法…一直归纳到S(n);这样我们就可以推导出关系式S(n)=S(n-1)+?
2、明确递归终止条件
递归既然有去有回,就必须有一个临界条件,当程序到达这个临界值就必须进行归来;否者就肯定会造成无线递归下去!
3、给出递归终止时的处理办法
根据上文中阐述的递归的工作原理,递归是通过栈来实现的;当程序到达临界条件时,后续必须进行出栈。了解函数的压栈和出栈过程,函数出栈也就是返回到上一个函数的调用处继续执行。例如求解F(n),递推式是F(n)=F(n-1)+F(n-2),终止条件F(1)=1,F(0)=0;它的流程是每次进行压栈F(n-1)、F(n-2),当达到终止条件时进行函数的出栈,那么返回什么值呢?根据递归的倒数第一步F(2)=F(1)+F(0)所以返回的是F(1)+F(0),也就是1.
分治法的基本思想
对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。【简单了说就是“分而治之”】
分治法所能解决的问题一般具有以下几个特征:
(1)该问题的规模缩小到一定的程度就可以容易地解决
(2)该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
(3)利用该问题分解出的子问题的解可以合并为该问题的解;
(4)该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题
解决该问题的步骤
问题:给定N个数据和待查找的数据x,采用二分查找算法来搜索x,输出x在N个数据中的位置
(1)解题思路
取数组中间索引mid=(begin+end)/2,比较待搜索值与中间值,如果待搜索值>中间值,则去中间索引的右边继续搜索,反之去左边;就这样循环下去,直到搜索到该值或者begin<end时终止程序。
/**
* @param arr 待搜索数组
* @param begin 头索引
* @param end 尾索引
* @param x 待搜索值
* @return 对应的下标
* 缺点:对于某种极端的情况需要一直进行搜索(比如1~100这种均衡的情况,如果刚好搜索1这个数,就需要搜索6次【50->25->12->6->3->1】
*/
public static int binarySearch(int[] arr, int begin, int end, int x) {
int mid = (begin + end) / 2;
while (begin <= end) {
if (arr[mid] > x) {
end = mid - 1;
} else if (arr[mid] < x) {
begin = mid + 1;
} else if (arr[mid] == x){
return mid;
}
mid = (begin + end) / 2;
}
return -1;
}
(2)分析以上算法思想的弊端
根据它的 int mid = (begin+end)/2 ,我们可以推算二分算法适用于什么场景;
假设一个数组为arr[1,2,3,4,5…,98,99,100] ,我们要找寻1这个值,那么需要几次找到呢?看下面的运行结果可以看出经历了六次循环调用才找到;如果找value=50,那么一次就能成功!所以这个调用多少次与mid的取值也有很大关系;
对二分查找算法进行优化
分析mid=(begin+end)/2,看出begin、end无法做出改变,那么只有对1/2进行改动;mid=begin + (begin+end) / {(value-arr[begin])/(arr[end]-arr[begin])},根据上文中找寻1,我们可以算出mid = 1。
根据上文进行分析,这个插值查找算法是对二分查找算法的改进。mid=begin + (begin+end) / {(value-arr[begin]) / (arr[end]-arr[begin])},这也就是插值查找算法。
-
优化思路如下:
-
上述二分思想f = 1 / 2 (f为变化率) -
将mid随着x值的大小做不断变化 f = (x - arr[begin]) / (arr[end] - arr[begin]) -
则 mid=f * (begin+end)
插值优化
/**
* @param arr 待搜索数组
* @param begin 头索引
* @param end 尾索引
* @param x 待搜索值
* @return 对应的下标
* 上述方法对于【1~100】这种均衡的极端情况不适用,所以需要进行优化处理
* 说到底是中间值的取法问题(好的中间值取法能够快速定位的搜索值),所以该二分查找优化的本质上是对中间值取法的优化
* 优化思路如下:
* 上述方法f = 1 / 2 (f为变化率)
* 将mid随着x值的大小做不断变化 f = (x - arr[begin]) / (arr[end] - arr[begin])
* 则 mid=begin + f * (begin+end)
*/
public static int binarySearch(int[] arr, int begin, int end, int x) {
int mid = (begin + end) * (x - arr[begin]) / (arr[end] - arr[begin]);
while (begin <= end && x > arr[begin] && x < arr[end]) {
if (arr[mid] > x) {
end = mid - 1;
} else if (arr[mid] < x) {
begin = mid + 1;
} else if (arr[mid] == x) {
return mid;
}
mid = begin + (begin + end) * (x - arr[begin]) / (arr[end] - arr[begin]);
}
return -1;
}
递归求解
递归方式
/**
* mid = (begin + end) / 2
* @param arr 待搜索数组
* @param begin 头索引
* @param end 尾索引
* @param x 待搜索值
* @return 对应的下标
*/
public static int binarySearch(int[] arr, int begin, int end, int x) {
if (begin > end) {
return -1;
}
int mid = (begin + end) / 2;
if (arr[mid] > x) {
return binarySearch(arr, begin, mid - 1, x);
} else if (arr[mid] < x) {
return binarySearch(arr, mid + 1, end, x);
} else {
return mid;
}
}
插值优化
/**
* int mid = begin + (begin + end) * [(x - arr[begin]) / (arr[end] - arr[begin])];
* @param arr 待搜索数组
* @param begin 头索引
* @param end 尾索引
* @param x 待搜索值
* @return 对应的下标
*/
public static int binarySearch(int[] arr, int begin, int end, int x) {
if (begin > end || x < arr[begin] || x > arr[end]) {
return -1;
}
int mid = begin + (begin + end) * (x - arr[begin]) / (arr[end] - arr[begin]);
if (arr[mid] > x) {
return binarySearch(arr, begin, mid - 1, x);
} else if (arr[mid] < x) {
return binarySearch(arr, mid + 1, end, x);
} else {
return mid;
}
}
测试结果
待搜索数组:int[] arr = {1, 3, 4, 5, 8, 11, 23, 77};
public static void main(String args[]){
int[] arr = {1, 3, 7, 5, 8, 6, 23, 77};
int result = binarySearch(arr,0,arr.length - 1,77);
System.out.println(result);
}
当搜索x = 3时,结果如下
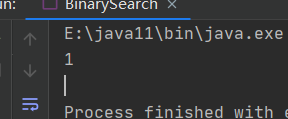
当搜索x = -11时,结果如下
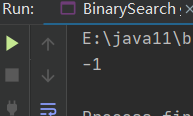
当搜索x = 156时,结果如下
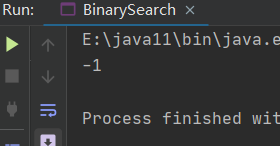
当搜索x =77时,结果如下
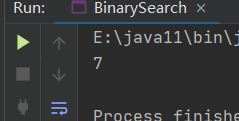
时间复杂度#
总共有n个元素,每次查找的区间大小就是n,n/2,n/4,…,n/2^k(接下来操作元素的剩余个数),其中k就是循环的次数。
由于n/2k取整后>=1,即令n/2k=1,
可得k=log2n,(是以2为底,n的对数),所以时间复杂度可以表示O()=O(logn)
空间复杂度#
递归的次数和深度都是log2 N,每次所需要的辅助空间都是常数级别的:
空间复杂度:O(log2N )




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通