bzoj3994 [SDOI2015]约数个数和

 传送门：http://www.lydsy.com/JudgeOnline/problem.php?id=3994

【题解】

这是一个比较重要的等式，反演常见套路之一：

那么有了这个等式我们就可以感性推导化简

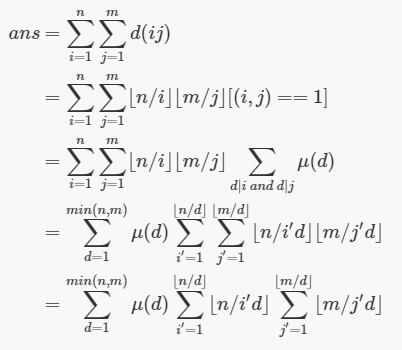
第一个等号到第二个等号待证。

然后我们又有，于是令

那么答案即为

接下来好像就是根号分段的事情了

暴力根号分段求下f，再暴力根号分段求每个询问即可。

安利一波，公式by leanote编辑器

复杂度O(nsqrt(n)+Tsqrt(n))

# include <stdio.h>
# include <string.h>
# include <algorithm>
// # include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
const int M = 5e5 + 10;
const int mod = 1e9+7;

# define RG register
# define ST static

int T, n, m;

const int F = 50000;
bool isnp[F + 10];
int p[F/3], pn=0, mu[F + 10];
ll s[F + 10], f[F + 10]; 

inline ll gF(int n) {
    ll ret = 0;
    for (int i=1, lst; i<=n; i=lst+1) {
        lst = n/(n/i);
        ret = ret + (ll)(n/i) * (lst-i+1);
    }
    return ret;
}

inline ll gG(int n, int m) {
    if(n > m) swap(n, m); 
    ll ret = 0;
    for (int i=1, lst; i<=n; i=lst+1) {
        lst = min(n/(n/i), m/(m/i));
        ret += (ll)(s[lst]-s[i-1])*(f[n/i]*f[m/i]);
    }
    return ret;
}

int main() {
    mu[1] = 1; 
    for (int i=2; i<=F; ++i) {
        if(!isnp[i]) {
            p[++pn] = i;
            mu[i] = -1;
        }
        for (int j=1; j<=pn && i*p[j] <= F; ++j) { 
            isnp[i*p[j]] = 1;
            if(i%p[j] == 0) {
                mu[i*p[j]] = 0;
                break;
            }
            mu[i*p[j]] = -mu[i];
        }
    }
    
    for (int i=1; i<=F; ++i) s[i] = s[i-1] + mu[i], f[i] = gF(i); 
    
    scanf("%d", &T); 
    while(T--) {
        scanf("%d%d", &n, &m);
        printf("%lld\n", gG(n, m));
    }

    return 0;
}