「6月雅礼集训 2017 Day7」三明治

【题目大意】

$1 \leq n,m \leq 400$

N字形表示：上图第1行第1个那种；Z字形表示上图第1行第2个那种。

【题解】

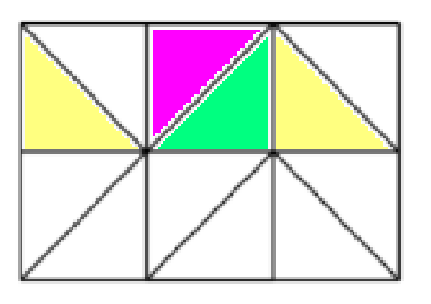
很容易得到结论：

考虑如果紫色比绿色先消去，那么黄色一定会比对应的白色先消去（这样才能消去白色）。

然后我们可以知道，设取走$(x, y)$靠左的正方形，要$L(x,y)$步，那么$L(x,y) \geq L(x,y-1)$，同理也有$L(x, y) \geq L(x, y+1)$。

然后我们对于这个就可以进行一行一行的dfs了，dfs的时候可能会搜到原来已经搜过的状态，我们令flag(x, y) = 2表示(x, y)已经被消掉过，flag(x, y) = 1表示(x, y)正在被消去的过程中，如果搜到flag(x, y) = 1，就说明形成了环状的依赖关系，答案就是-1. 如果flag(x, y) = 2，表示之前已经消过了，返回0即可。

然后。。卡卡常就过了。

判断字符比判断bool慢，所以用bool代替char的map；然后因为判断新的$(x', y')$在不在边界里要判断很多，如果在边界外也返回0，所以我们直接设置他们的flag = 2即可。

然后就过了。

# include <stdio.h>
# include <string.h>
# include <iostream>
# include <algorithm>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;

const int N = 4e2 + 10, M = 2e5 + 10, inf = 1e9;

# define ST static
# define RG register

int n, m;
ST bool mp[N][N];
ST int f[N][N], g[N][N];
ST int flag[N][N];
const int dx[] = {1, 0, -1, 0}, dy[] = {0, 1, 0, -1};

inline int dfs(int x, int y, int face) {
    if(flag[x][y] == 1) return inf;
    if(flag[x][y] == 2) return 0;
    flag[x][y] = 1;
    int ret = 1;
    if(mp[x][y]) {
        ret += dfs(x + dx[face], y + dy[face], face);
        face ^= 3;
        ret += dfs(x + dx[face], y + dy[face], face);
    } else {
        ret += dfs(x + dx[face], y + dy[face], face);
        face ^= 1;
        ret += dfs(x + dx[face], y + dy[face], face);
    }
    flag[x][y] = 2;
    if(ret > inf) ret = inf;
    return ret;
}
    

int main() {
//    freopen("sandwich.in", "r", stdin);
//    freopen("sandwich.out", "w", stdout);
    cin >> n >> m;
    for (RG int i=1; i<=n; ++i) {
        getchar();
        for (RG int j=1; j<=m; ++j) mp[i][j] = (getchar() == 'N');
    }
    for (RG int i=1; i<=n; ++i) {
        memset(flag, 0, sizeof flag);
        for (RG int j=1; j<=m; ++j) flag[0][j] = flag[n+1][j] = 2;
        for (RG int j=1; j<=n; ++j) flag[j][0] = flag[j][m+1] = 2;
        for (RG int j=1; j<=m; ++j) f[i][j] = min(inf, f[i][j-1] + dfs(i, j, 3));
    }
    for (RG int i=1; i<=n; ++i) {
        memset(flag, 0, sizeof flag);
        for (RG int j=1; j<=m; ++j) flag[0][j] = flag[n+1][j] = 2;
        for (RG int j=1; j<=n; ++j) flag[j][0] = flag[j][m+1] = 2;
        for (RG int j=m; j; --j) g[i][j] = min(inf, g[i][j+1] + dfs(i, j, 1));
    }
    for (RG int i=1, ans; i<=n; ++i, puts(""))
        for (RG int j=1; j<=m; ++j) {
            ans = min(f[i][j], g[i][j]);
            if(ans == inf) printf("-1 ");
            else printf("%d ", ans << 1);
        }
    return 0;
}