[Trick] 格路记数 - 反射容斥

Perface

模拟赛不会被冲烂了。

Problem I

从 $(0,0)$ 到 $(n,m)$ 方案数。

解法：
$C(n+m,m)$。

Problem II

从 $(0,0)$ 到 $(n,m)$ 方案，但是不能经过 $y=x+b$ 的直线。

解法：
考虑映射法。

以一条路径第一次碰到直线的位置为起点，之后所有的路线和 $y=x+b$ 对称，这样可以不重不漏的映射完每一条路线。我们发现，这些路径的终点都是 $(m-b,n+b)$。

答案为:$C(n+m,n)-C(m+n,m-b)$

Problem III

从 $(0,0)$ 到 $(n,m)$ 方案，但是不能经过 $y=x+b$ 和 $y=x+c$ 的直线。

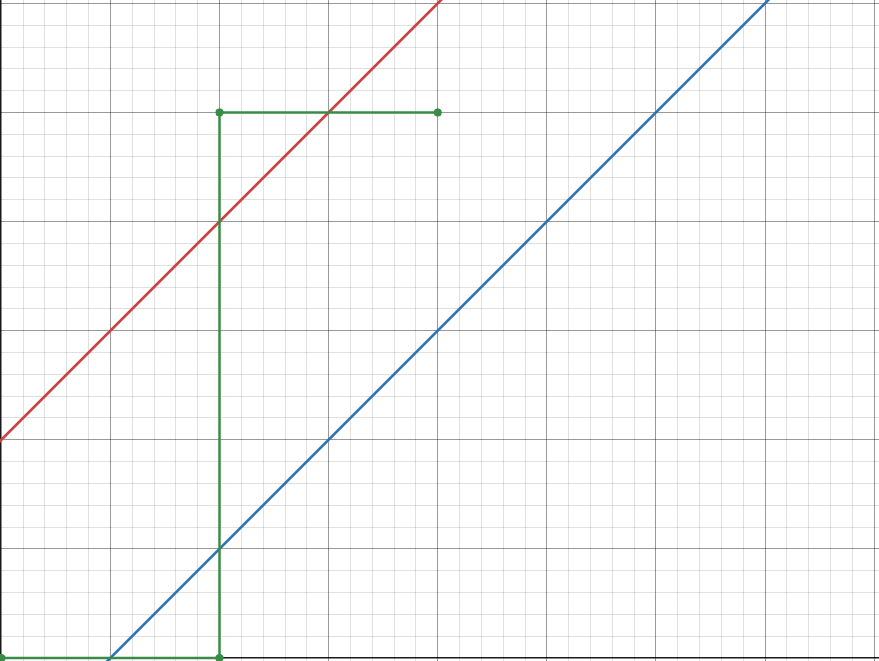
当第一次碰到蓝色线段时，我们进行翻折。

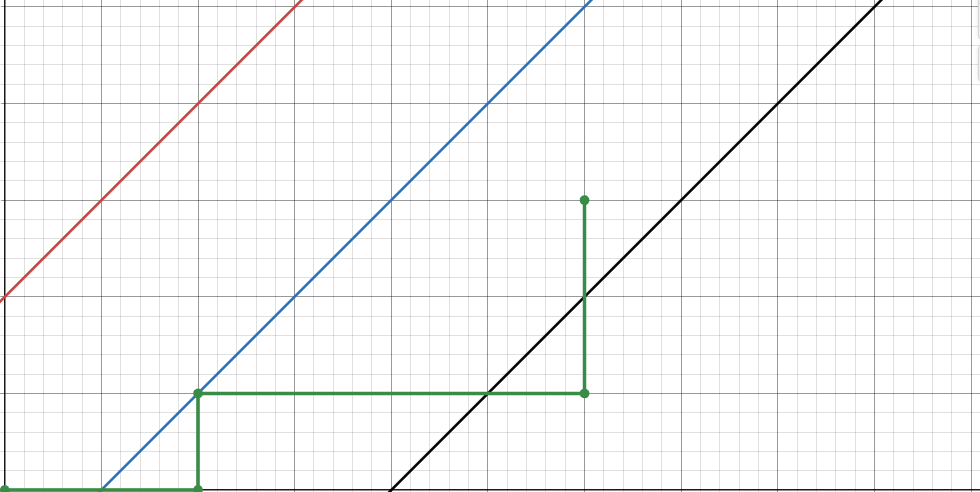
碰到红色线段，也就是对称的黑色线段时，再次翻折。

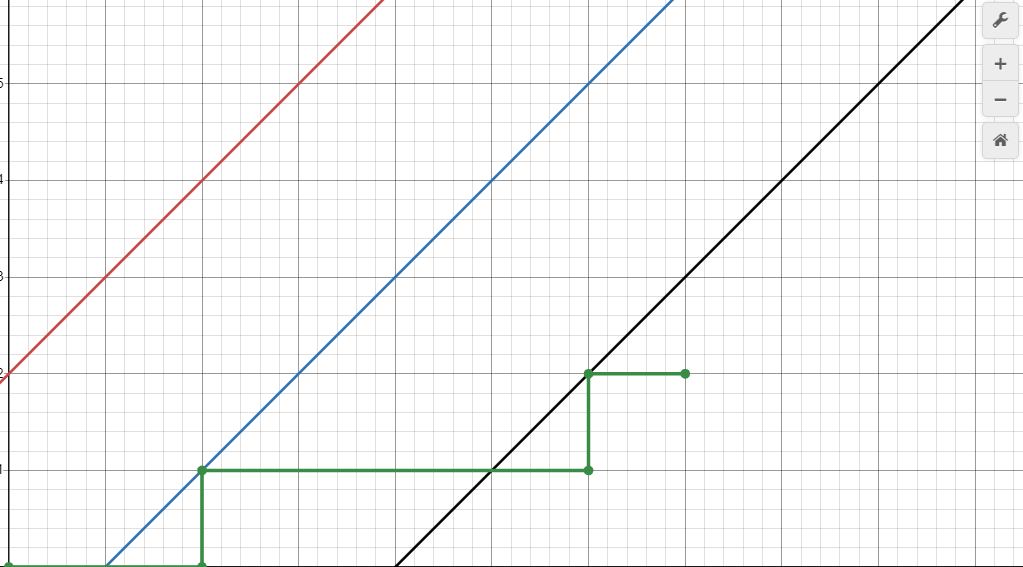
因此，穿过两次线段的我们也映射完了。

观察一下，本质上就是将终点与线段进行对称。

对于一条线依次经过了 $y=x+b$,$y=x+c$，记反射序列为 $bc$，但是如果经过一条线两次 $bbc$ 我们也看做 $bc$，因为我们记第一次碰到折线为对称点做到不重不漏。

那么，答案就是 $ans=\empty-b-c+bc+cb-bcb-cbc+bcbc+cbcb-...$ (容斥原理)

因此，我们需要推出一个对称点的公式，快速求出 $cbcbcb$ 点的对称坐标。

不难发现，本质上就是线和终点关于线对称，不清楚的直接看图：

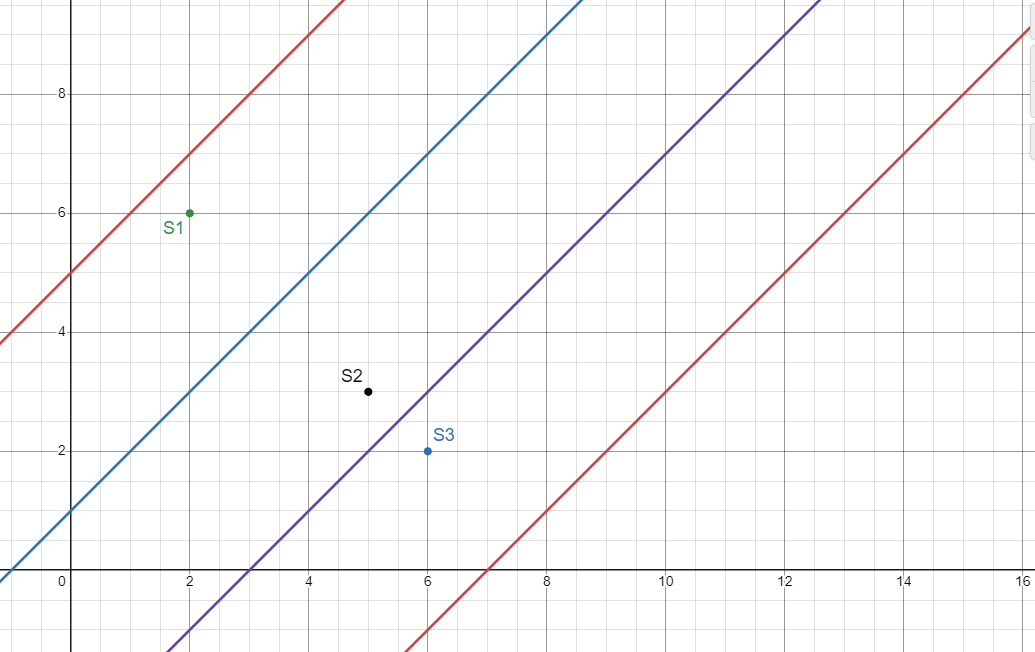
容易知道一个点 $(x,y)$ 对于 $y=x+b$ 对称点为 $(y-b,x+b)$，直线为 $y=x+c$ 变为 $y=x+2b-c$，我们只需要动态维护两条直线然后模拟即可。

考虑边界情况。不难发现每两次坐标会变化 $2|b-c|$，也就是时间复杂度为 $O(\frac{n+m}{|b-c|})$。

被创飞了。

注意到这些点都在一条线上，也就是 $x+y$ 始终不变，预处理这一条线的组合数即可。

inline void mirror(ll &x,ll &y,ll b){y-=b,x+=b;swap(x,y);}
inline void mirror(ll &c,ll b){c=2*b-c;}
inline ll P(ll x){return C[min(x,n+m-x)];}
ll g(ll b,ll c)
{
	ll x=n,y=m;
	ll sum=0,cur=1;
	while(x>=0&&y>=0)
	{
		sum=(sum+mod+P(x)*cur)%mod;
		mirror(x,y,c);
		mirror(b,c);
		swap(b,c);
		cur=-cur;
	}
	return sum;
}
inline ll f(ll b,ll c){return m-n>=b&&m-n<=c?(-P(n)+g(b-1,c+1)+g(c+1,b-1)+mod)%mod:0;}