网络流 & 二分图基本知识

重拾网络流，真正感受了它的妙处。
这一篇重点在于证明，应用可以看我以前写的。

二分图

二分图是什么

简单来说，你可以把一个图分成两部分点，两部分点间有边相连，但是每部分点两两间没有边相连。

二分图判定的充要条件

一个图是二分图的充要条件是不存在奇环。
充分性：对于任意一个二分图，由于每个部分内部都没有边，因此一个点从出去自己部分再回到自己部分都是经过两条边，充分性得证。

必要性：对于一个没有奇环的图，随便钦定一个点为黑色，然后与它相连的点为白色，与白色相连的点为黑色，将整个图染色，我们发现出现同色点之间存在一条边的条件就是存在奇环，所以必要性得证。

怎么判定

• 模拟染色即可
• 使用扩展域并查集，将每个点分成黑白两个点，然后两个点连边就是黑白合并，白黑合并，如果两个点同色已经在同一集合中，说明不是二分图，这个技巧让我们可以动态加边判定二分图，删边可以去了解一下线段树分治。

二分图的最大匹配

二分图最大匹配的意思就是在每个点只被覆盖一次的情况下选最多的边。
如图，这个图的最大匹配是 $4$。

那么这个怎么算呢？
我们引入两个概念：

• 交替路：从一个点出发，每次交替走一条匹配边和一条非匹配边
• 增广路：从一个点出发走交替边，这条交替路未匹配边比匹配边多一条。

匈牙利算法的思想就是不断增广，找到最大匹配。
因为增广路把所有交替边和非交替边一反就是一组新的方案。

贪心的不断增广，一定可以找到正确答案。
如果你学了网络流，这里可以这样解释，对于未匹配前，我们所有的点都是有向边，即 $U\to V$。对于选过的边，我们建一条 $V\to U$ 的反边，找到合法方案。

匈牙利算法事件复杂度 $O(nm)$，可以建网络流模型达到 $O(n\sqrt m)$。

König 定理

最小点覆盖：选最少的点，满足每条边至少有一个端点被选。
二分图中，最小点覆盖 $=$ 最大匹配。

感性理解：如果在最大匹配选的点集中，有一条边两点都没有被选，那么这一定是一个新的匹配。

现在我们来构造并证明这个定理。

Step 1.

把所有边都剔除，只剩下最大匹配选的边，求这些边的最小点覆盖，可以得到：最小点覆盖 $=$ 最大匹配。所以原图的最小点覆盖 $\ge$ 最大匹配。我们来证明等号成立。

Step 2.

我们从所有右边没有匹配边的点开始走交替路，给走过的节点都打上记号。
我们选右边没有标记的点和左边有标记的点。
因为原图中不存在增广路，所以所有的路径都是从右边开始，右边结束。
因此，左边走过的点一定是某条最大匹配边的点。右边没走过的点也是某条最大匹配边的点。
考虑到没有任何一条最大匹配边能右边没有标记且左边有标记，一个点不会有两条匹配边，因此我们刚好选中了最大匹配那么多点。

Step 3.

现在证明这些点恰好覆盖了所有边。
是否存在一条边，左右都没有被选上呢？
首先，如果是匹配边，那么它肯定被选了。
对于非匹配边，它没有被选中仅当它右边有标记且左边没有标记。这是不存在的，因为非匹配边如果右边没有被匹配才会被打上标记，然后这条边就会被走并且打上左边的标记。
得证。

最大独立集

要求在二分图中选最多的点，且不存在任何一对匹配。
定理：最大独立集=点数-最小覆盖点

在最小覆盖中，每条边都被至少有一个顶点被选，所以取反就使得每条边至多一个点被选。
在最大独立集中，每条边至多一个点被选，取反后每条边至少一个点被选。
因此这两个东西可以互相取反。

可以看我以前写的：二分图练习

至此，二分图部分结束。

网络流

什么是网络最大流？

在一张网络上，起点有无限流量，每条边有流量限制，问重点流量最大是多少。

怎么实现？

一般的贪心，我们找到一条能流到终点的路就流，这就叫增广路。
我们可以贪心的增广得到最大流。吗？
不一定。

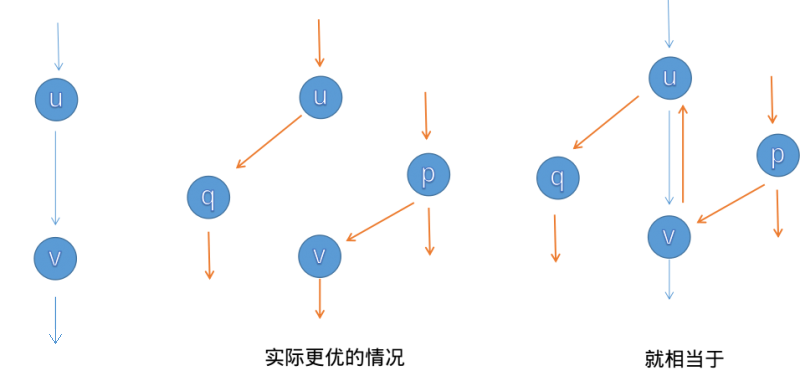
我们需要引入“反悔”边，反边，这样我们如果走出左边那种不优路径的话，如图三，我们会进行“反悔”，可以证明，反悔完的所有方案与原方案都是一一对应且等价的。

我们可以一直 dfs 增广。但这是很蠢的，时间复杂度是 $O(\text{流量大小\times m})$，非常鬼畜。

EK 算法

算法步骤：

bfs 增广，找到增广路就退出。
时间复杂度 $O(nm^2)$。

引理：增广最短路不降

在不断寻找增广路的时候，最短路的单调不降的。
考虑反证法，设第一个使最短路变短的点 $v$，使得 $s\to v$ 路径经过增广以后路径长度变短。即 $d'_v<d_v$，$d'_v=d'_u+1$

不妨设 $v$ 是从 $u$ 走过来的。我们有意设了第一个满足变短的点，因此 $u$ 并不变短，即 $d'_u\ge d_u$。

我们可以证明，增广前不存在 $u\to v$ 这条边，因为存在的话，可以发现 $d_v\le d_u+1\le d'_u+1=d'_v$，与假设相矛盾。

所以 EK 肯定流过了 $(v,u)$ 这条边，而且这是一条满流的边，因为是 bfs 增广，所以 $v\to u$ 在原图最短路上，即 $d_u= d_v+1$，得 $d_v= d_u-1$。因为 $d_u-1\le d'_u-1=d'_v-2$，与假设矛盾，得证。

定理：最多增广次数为 $O(nm)$

我们设一条边成为关键边，即这条边出现在最短路上，增广后被清空。不妨设为 $u\to v$，即 $d_v=d_u+1$。这样它会被 bfs 遍历到。这时候，$u\to v$ 将会从图中消失，变为 $v\to u$。

考虑 $u\to v$ 重新出现，即 $v\to u$ 在增广路上。此时：$d'_u=d'_v+1$

我们知道 $d'_u\ge d_u$，$d'_v\ge d_v$。

所以 $d'_u\ge d'_v+1\ge d_v+1=d_u+2$

所以每条边最多做关键边 $\dfrac{n-1}{2}$ 次，正反边都算，满打满算总共增广次数为 $O(nm)$。

时间复杂度

考虑到每次遍历图为 $O(n+m)$，总时间复杂度易得为 $O(nm^2)$。

Dinic 算法

最主流、最推荐的算法，CCF 唯一指定网络流标准算法，绝对不会卡！
时间复杂度是 $O(n^2m)$。

流程

我们知道，EK 的缺陷在它太笨了，每次找到增广路就从头再找一次。
所以我们要改造 EK，我们从原图跑一次 bfs 跑到 $t$，记录下每条路径，然后做聪明的增广，也就是不在到每个点最短路上的边全是废边（暂且认为），然后贪心的在这个分层图上增广，能流就流。

这样改造完还是 $O(nm^2)$ 的，因为没有改变什么实质，非常蠢笨。下面有几个优化。

常数优化

如果访问到一个点它退回来一个流量 $0$ 时，那么这个方向就是废的，可以给它打上飞舞标记，当前轮不走这条路。

必须的优化

当前弧优化，使 Dinic 有质的飞跃。
具体的，走到一个点，如果前面某些点流满了，就不遍历了，很简单，没用。

一个看似无用的优化，却让我们算法有质的提升！
这让我们笨笨的算法变成聪明算法了！每次它都会聪明的找到一条合法的增广路！

最聪明的优化在于，每次增广后，它会直接剔除掉一个点，而不是边！那么，每次增广最坏是 $O(m)$ 的，$n$ 个点，最短路长度上界为 $n$，时间复杂度是 $O(n^2m)$。

总结

在最大流中，Dinic 是最基本的算法。

最大流最小割定理

对于一对 $(s,t)$，定理：最大流 = 最小割

Part 1

证明：任意一个流小于任意一个割
是这样的，对于任意一个流来说考虑自己流过量的大小就行了，但是割考虑的就多了

显然的，对于一个流来说，这些流量只会小于等于流量上界，最小割割掉的是流量上界那么多，所以得证。

Part 2

证明：只有在最大流的时候，最大流可以与一个割取等号。

因为是最大流，显然的，不存在任何一条增广路，使得 $s$ 到 $t$ 有流量。
我们把所有满流的边拎出来，就变成了一个割边集，这是一个合法的割。

Part 3

证明：最大流等于最小割
我们知道，任意流量小于最大流。任意割集大于流量，大于等于最小割。割集又可以和最大流取等，所以最小割等于最大流。

Hall 定理

这个东西可以用最大流最小割一秒明白。
设左边点为 $V_1$，右边点为 $V_2$。
我们知道，把二分图转为网络流模型后，若求解最小割，不难发现，我们只会割 $s$ 与左边点的边或者 $t$ 与右边点的边(选择割掉中间的边是个非常笨的选择)，我们假如保留的左边的点集 $S$，那么我们显然要割掉右边与 $S$ 相连的所有边 $N(S)$，即 $\min(|V_1|-|S|+|N(S)|)$。这个东西就是扩展 Hall 定理。当时时刻刻满足 $|S|=|N(S)|$，就是 Hall 定理。根据最小割最大流容易理解。

最大权闭合子图

一个经典应用。
问：给出一张有向图，你要在里面选一个点集，使得任意一个点的出边都在点集内，每个点有权值，求权值和的最大值。

正难则反，考虑选上所有的点，然后舍弃掉一些。

建立超级原点和超级汇点，将超级原点与所有权值为正的点连边权值为正点权值，将所有权值为负的点和汇点连边，权值为其绝对值。原网络的边权值设为 $INF$。

我们只关注正权值。最终的权值就是所有与 $s$ 相连的边。

我们看看割掉这个图的一条边意味什么：

• 割掉 $s$ 的边：删去一个正点的权值
• 割掉 $t$ 的边：加上一个负点的权值

我们看看不割边是否合法：说明 $s$ 能到 $t$，你必须选择一些负边的权值，或者删掉某个正点的权值，这是不合法的，我们只需要求解最小割即可。

费用流

费用流中 Dinic 就是飞舞，EK 更快，因为存在相同费用的增广路很少。

概念

现在每条边流过一单位流量要给钱，求得到最大流同时给钱最少。

基本算法

将 Dinic 或者 EK 中的 bfs 找同距离的增广改为找同费用是增广路，改为 spfa 求最短路即可，因此 Dinic 很飞舞，基本不会出现费用相同的增广路。

这实现是非常简单的，若增广次数为 $f$ (上限我哪知道，没人分析，但是不会超过最大花费，你可以看做是花费大小），则时间复杂度为 $O(fnm)$。

下面我们来讲解原始对偶算法，复杂度是 $O(fm\log m)$。

过程

局限性一眼顶针，spfa 太飞舞了，于是，dij 启动！
我们知道 dij 不能跑负边，而费用流有反向边因此必然存在负边，怎么办呢？

不妨回忆一下我们以前学的 Johnson 全员最短路，对于每个点加上一个势能，给它改造成正的就能跑 dij 了。

首先，如果有负边，我们可以先跑一次 BF，把它改成正的。
具体的，建立超级原点向每个点连边得出最短路 $h$，将一条 $u\to v$ 的边 改为 $w(u,v)+h_u-h_v$。

然后我们把视角转到跑 EK 中，刚刚跑完第一次 dij。

此时我们看看原来的图发生了什么变化：某些正向边消失，某些反向边出现，我们发现反向边是个非常难搞的东西，此时我们需要修改 $h$ 函数来对整个图大改。

直接给出结论：只需一个操作，就是把所有 $h_i$ 加上对于的 $d_i$ 即可，$d$ 是刚刚 dij 跑出来的最短路数组。

我们看看这为什么是正确的。

首先，对于没有被访问的边，对于 $u,v$，有 $d_u+h_u-h_v+w(u,v)\ge d_v$

移项易得 $(d_u+h_u)-(d_v+h_v)+w(u,v)\ge 0$，因此没有任何问题。

对于被访问的边，那么这时候会出现反向边，基于在最短路上的边，我们知道，此时有 $d_u+h_u-h_v+w(u,v)= d_v$，移项得 $(d_u+h_u)-(d_v+h_v)+w(u,v)= 0$。

那么，我们看看反向边，就是 $(d_v+h_v)-(d_u+h_u)-w(u,v)$，这也是 $0$，所以我们可以放心跑 dij 了！

其实费用流时间复杂度还是很玄学……