abc353f 题解

大分讨，由于没注意到细节挂大分。

下面称大小为 \(n\times n\) 的为大格子，\(1\times 1\) 的为小格子。把 \(n\times n\) 个小格子组成的正方形称为一个部分。

分析

我们先来讨论一般情况。

思考一

对于 \(n\ge3\) 的一般情况，如果要求任意两个大格子到对方的距离最小，怎么做？

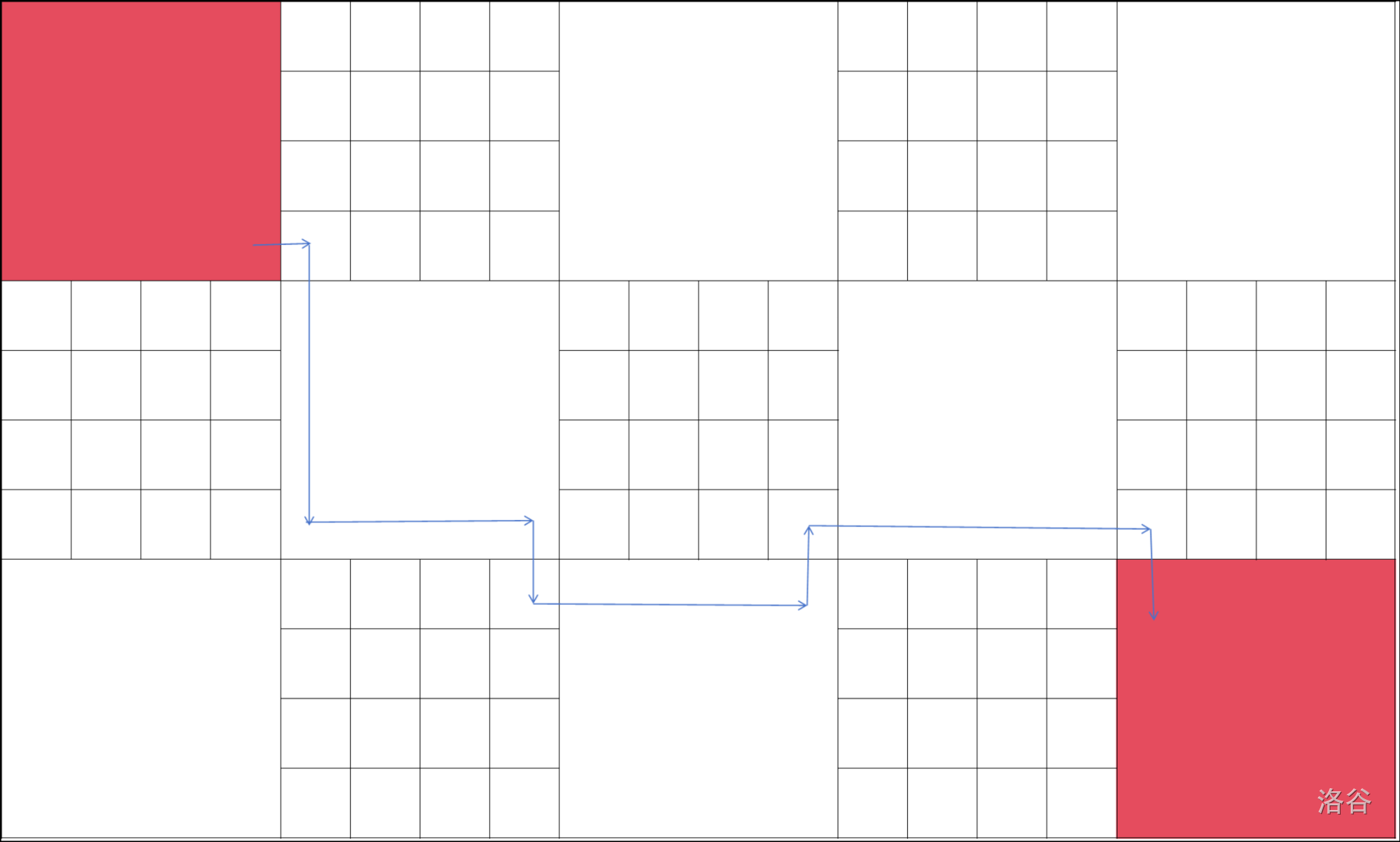
根据贪心，我们不难把行走拆为两个部分：

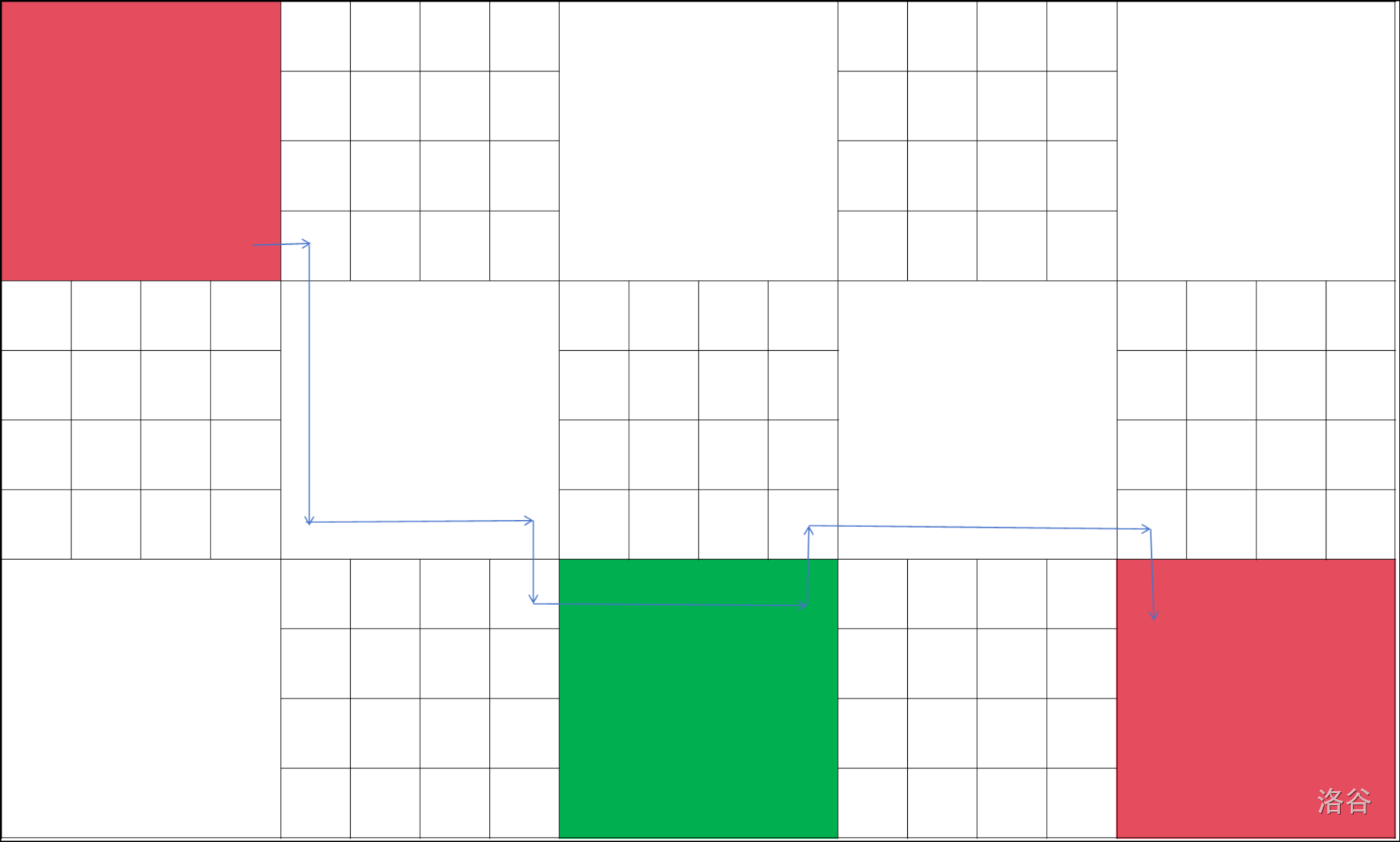
• 部分一
  从左上角红色格子到绿色格子部分。

• 部分二
  从绿色格子到右下角红色格子部分。

我们发现，假设如果从任意一个点到另一个点，它的路径是这样的：

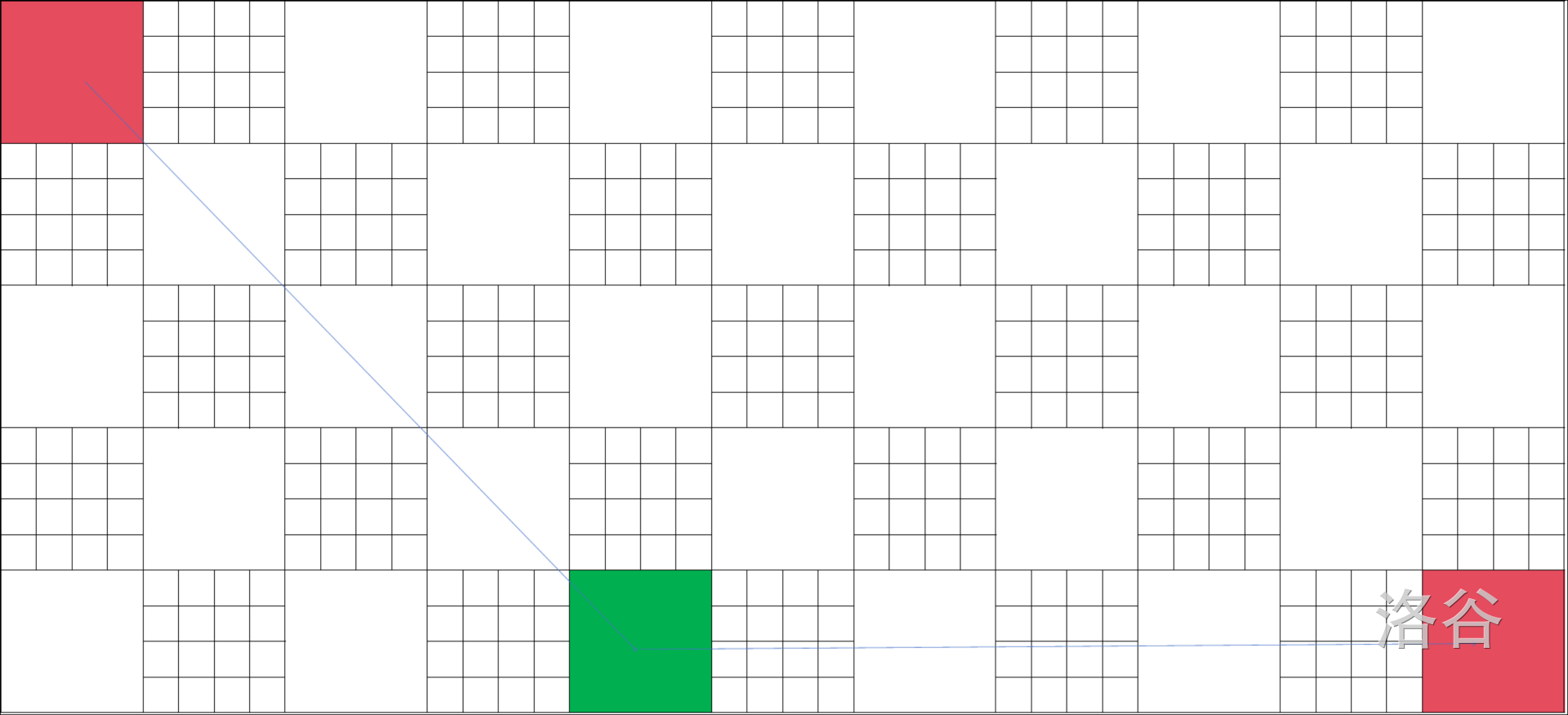
每一部分贪心的走。我们发现相邻两个大格子需要走两次，然后分析一下，不难得出距离公式：
\(D(sx,sy,tx,ty)=2\times \max(|sx-sy|,|tx-ty|)\)。

思考二

如果起点、终点在小格子里怎么办？

没有关系。我们这些情况转化为大格子的情况。

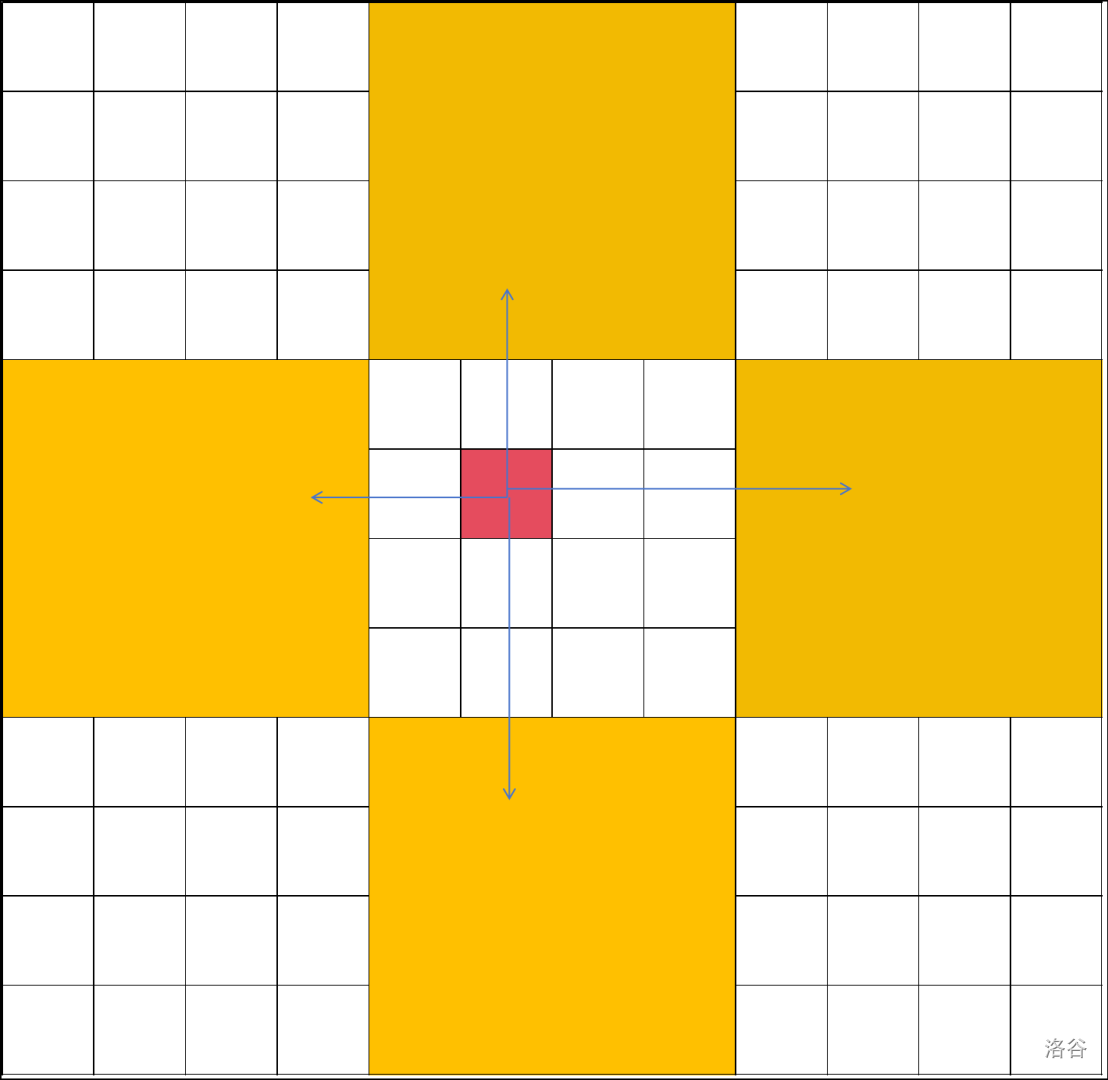
然后计算权值时再加上蓝色线条部分的长度即可。
这里最多会计算 \(4\times 4=16\) 次。

思考三

如果在起点，终点在同一部分里，怎么办？

对于在大格子，答案显然是 \(0\)。

对于小格子，似乎是两点之间的曼哈顿距离？
不对！这就是笔者挂分的点！

它还可以绕出去……具体可以看图。

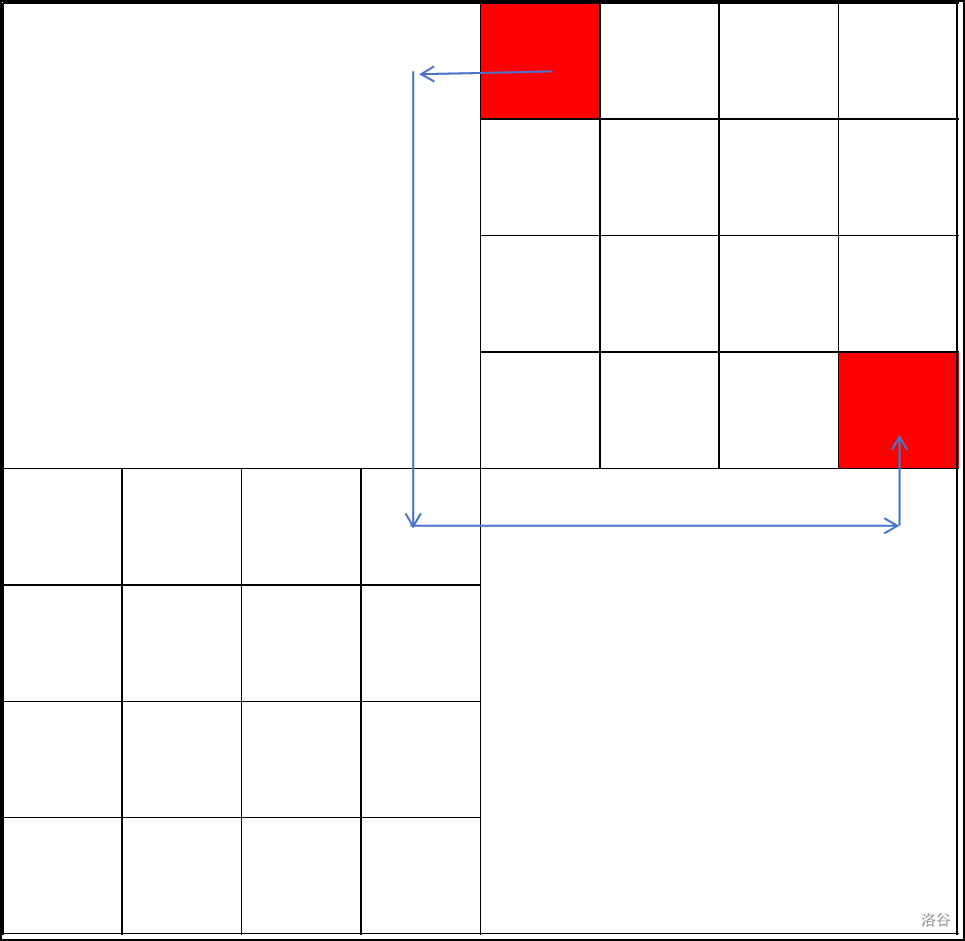
所以要归并到上面的情况一起计算。

思考四

似乎做完了？
不，还有特殊情况。

• \(n=1\)

输出曼哈顿距离即可。

• \(n=2\)

这个改变的地方在这里：

从绿色格子到终点的部分，我们选择直接穿过所有格子。

因为绕两次需要穿过四次格子，直接穿过却只需要三次。
特判一下即可。

至此，这道题就完工了。

Code

#include<bits/stdc++.h>
#define N 600005
#define ll long long
using namespace std;
struct node{
	ll x,y;
};
ll n;
ll sx,sy,tx,ty;
ll d(ll sx,ll sy,ll tx,ll ty)
{
	ll P=max(abs(sx-tx),abs(sy-ty));
	if(n^2) return P*2;
	else return min(abs(sx-tx),abs(sy-ty))*2+(abs(abs(sx-tx)-abs(sy-ty)))/2*3;
}
node B(ll x,ll y)
{
	node tmp;
	tmp.x=x/n;
	tmp.y=y/n;
	return tmp;
}
node S[5],T[5];
ll ds[5],dt[5];
ll sn=1,tn=1;
ll ans=4e18;
ll w[5];
int main()
{
	scanf("%lld",&n);
	scanf("%lld%lld%lld%lld",&sx,&sy,&tx,&ty);
	if(n==1)
	{
		printf("%lld",abs(sx-tx)+abs(sy-ty));
		return 0;
	}
	S[0]=B(sx,sy),T[0]=B(tx,ty);
	if(S[0].x==T[0].x&&S[0].y==T[0].y)
	{
		if((S[0].x&1)==(S[0].y&1)) ans=abs(sx-tx)+abs(sy-ty);
		else
		{
			printf("0");
			return 0;
		}
	}
	if((S[0].x&1)==(S[0].y&1))
	{
		sn=4;
		S[1]=(node){S[0].x-1,S[0].y};ds[1]=abs(S[0].x*n-sx)+1;
		S[2]=(node){S[0].x,S[0].y-1};ds[2]=abs(S[0].y*n-sy)+1;
		S[3]=(node){S[0].x+1,S[0].y};ds[3]=abs(S[0].x*n+n-sx);
		S[4]=(node){S[0].x,S[0].y+1};ds[4]=abs(S[0].y*n+n-sy);
	}
	else S[1]=S[0];
	if((T[0].x&1)==(T[0].y&1))
	{
		tn=4;
		T[1]=(node){T[0].x-1,T[0].y};dt[1]=abs(T[0].x*n-tx)+1;
		T[2]=(node){T[0].x,T[0].y-1};dt[2]=abs(T[0].y*n-ty)+1;
		T[3]=(node){T[0].x+1,T[0].y};dt[3]=abs(T[0].x*n+n-tx);
		T[4]=(node){T[0].x,T[0].y+1};dt[4]=abs(T[0].y*n+n-ty);
	}
	else T[1]=T[0];
	for(int i=1;i<=sn;i++)
	{
		for(int j=1;j<=tn;j++)
		{
			ll dis=d(S[i].x,S[i].y,T[j].x,T[j].y);
			ans=min(ans,dis+ds[i]+dt[j]);
		}
	}
	printf("%lld",ans);
	return 0;
}