[多项式] FFT小计
引入
给出两个多项式 \(A,B\) ，计算它们相乘的结果。
我们能轻易写出 code：
for(int i=0;i<=n;i++)
for(int j=0;j<=n;j++)
C[i+j]+=A[i]*B[j];
然后超时了。
FFT 是一种将多项式乘法优化成 \(O(n\log n)\) 的神仙算法。
接下来会介绍傅里叶的四个神仙 trick。
分析
上面的式子没有任何优化空间。
什么意思呢？就是怎么乱搞都优化不了。于是我们看看天才算法是怎么搞的。
点值表示法
我们知道 \(n\) 个点确定一条 \(n-1\) 次多项式。
所以我们把多项式转到平面上。
我们随便取 \(2n+1\) 个点，先在 \(A\) 中计算出这些点，表示成 \((x,y_A)\)，然后在 \(B\) 中计算出这些点：\((x,y_B)\) ，然后我们就能很容易计算出 \(y_C=y_A\times y_B\) 。然后我们用 \(n\) 个点确定一条多项式。
天才思路！但是是不是有什么不对的地方？
计算一个点是 \(O(n)\) 的，然后有 \(n\) 个点要计算...时间复杂度 \(O(n^2)\)。
如果只是随便取点，就是低估了傅里叶的上限了。
递归计算
我们想想我们有没有知道一个点 \(x_1\) 的值，就能马上另一点的值呢？
我们先来看二次函数 \(f(x)=x^2\) ：
如果知道 \(f(5)=25\)，马上就能知道 \(f(-5)=25\)。
再来看看三次函数 \(f(x)=x^3\)，和二次函数一样，但是加个负号就行，说人话就是奇偶函数。
我们推广到多项式这一般形式：
\(A(x)=16x^5+22x^4+7x^3+5x^2+13x+8\)
我们把奇偶次数分开一下：
假设我们算出 \(x\) 点的取值为 \(p+q\) ，那么 \(-x\) 点的取值不就是 \(q-p\) 吗！
也就是说，我们现在只需要取 \(\frac{n}{2}\) 这么多点就行了。
然后能不能继续拓展？
这个看起来能递归的样子：
我们定义函数 \(D(A)\) 表示给这个函数一个 \(n\) 次的多项式，它会返回 \(n+1\) 个点和它们的取值。
我们看看这个式子：
我们看看括号的式子，我们把 \(x^2\) 看成 \(x\) ，这不就是子问题吗！
所以递归求解就行了！
举个例子，假设我们计算 \(x_1,x_2,x_3,x_4,-x_1,-x_2,-x_3,-x_4\)，我们计算子问题 \(x_1^2,x_2^2,x_3^2,x_4^2\) 的取值就行了。
等等，是不是有些问题？
新要计算的数全是平方项，都是正数，不存在相反数，所以递归不成立(悲)。所以难道就只能结束了吗？
取点
这里是 FFT 算法最天才的部分。
我们想想刚才的递归。
假设第一轮取的四个数是 \(x_1,x_2,-x_1,-x_2\)
那么第二轮的两个数是 \(x_1^2,-x_1^2\)
最后一轮取的数就是 \(x^4\)，好消息是，最后一轮这个 \(x\) 我们可以随便取，所以我们令 \(x=1\)。
我们往下推，\(x^4=x_1^2\)，所以我们取 \(x_1=1\)，所以我们已经确定了两项：\(x_1=1,-x_1=-1\)。
我们看另一部分， \(x_2^2=-x_1^2=-1\)，所以 \(x^2_2=-1\) 这不显然无解吗。
所以傅里叶最天才的部分就到了，实数部分没有，取虚数不就行了！
所以 \(x_2=i\)。
我们继续看上面的例子。
我们计算子问题 \(x_1^2,x_2^2,x_3^2,x_4^2\) 的取值。
假设我们满足 \(x_2^2=-x_1^2,x_4^2=-x_3^2\)
这个时候我们计算 \(x_1^4，x_3^4\) 就行。
最后，我们发现，其实我们就是解一个方程： \(x^8=1\)
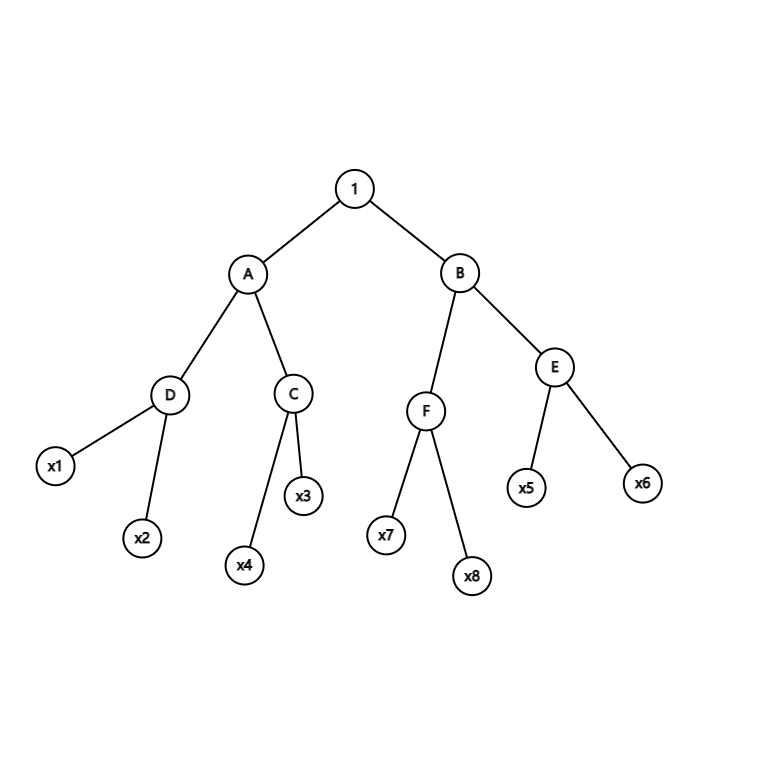
整个流程是一棵二叉树。
我们想要对于每个节点，它的两个叶子节点成相反数，当前节点的值等于叶子节点值的平方。
看这个图，也可以说，FFT 一次性就是在处理每一层的信息，我们也能感受到 FFT 的时间复杂度：\(O(n\log n)\) 。
问题来了：这些数怎么取呢？
这部分不是 FFT 重点，请看 这个。
知道单位根以后，这部分就很简单了。
我们看看这个图：
\(A:\omega_2^0(=1),B:\omega_2^1\)
\(D:\omega_4^0(=1),C:\omega_4^2,F:\omega_4^1,E:\omega_4^3\)
所以，对于任意一个点，若是 \(\omega_n^k\)，那么它的儿子分别是 \(\omega_{2n}^k,\omega_{2n}^{k+n}\)。
于是，我们在 \(O(n\log n)\) 的优秀时间复杂度内完成了取点。
点值转多项式
这个怎么办呢？
拉插的 \(O(n^2)\) 明显无法接受。
我们知道最终的点值表示：\(G(k)=\sum\limits_{i=0}^{n-1}F(i)(\omega_n^k)^i\)
emm这个正推很搞，直接给出结论： \(F(k)\times n=\sum\limits_{i=0}^{n-1}(\omega_n^{-k})^iG(i)\)
我们反证。
我们把 \(G(i)\) 给带入一下。
\(\sum\limits_{i=0}^{n-1}(\omega_n^{-k})^iG(i)\)
\(=\sum\limits_{i=0}^{n-1}(\omega_n^{-k})^i\sum\limits_{j=0}^{n-1}F(j)(\omega_n^i)^j\)
\(=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1}\omega_n^{-ik}F(j)\omega_n^{ij}\)
\(=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1}F(j)\omega_n^{i(j-k)}\)
我们分类讨论一下。
-
\(1.j=k\)
此时原式子等价于 \(nF(k)\)。 -
\(2.j\ne k\)
我们定义 \(p=j-k\)。
原式等价于
\(=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1}F(p+k)\omega_n^{ip}\)
我们把 \(j\) 枚举提前，相当于枚举 \(p\) 。
\(=\sum\limits_{j=0}^{n-1}\sum\limits_{i=0}^{n-1}F(p+k)\omega_n^{ip}\)
我们看这个部分。
\(\sum\limits_{i=0}^{n-1}F(p+k)\omega_n^{ip}\)
\(=F(p+k)\sum\limits_{i=0}^{n-1}\omega_n^{ip}\)
玄学的地方就在这里：
设 \(S=\sum\limits_{i=0}^{n-1}(\omega_n^{p})^i\)
则 \(\omega_n^pS-S=\omega_n^n-\omega_n^0=0\)
由于 \(p\ne 0\)，所以 \(\omega_n^p\ne 1\)，所以 \(S=0\)。所以这一部分没有贡献。
所以我们看到这个公式：
\(F(k)\times n=\sum\limits_{i=0}^{n-1}(\omega_n^{-k})^iG(i)\)
\(\times n\) 那一项我们最后消掉即可。然后我们发现这个式子怎么长得和得到的式子这么像啊，所以我们直接对 \(G\) 做转点值，但是系数是 \(\omega_n^0,\omega_n^{-1},\omega_n^{-2}...\omega_n^{-(n-1)}\)。这与 \(\omega_n^0,\omega_n^{n-1},\omega_n^{n-2}...\omega_n^{1}\) 等价。所以可以进行 \(FFT\) 加速。
还是详细写一下这里：
举个例子：
\(\omega_4^{0},\omega_4^{-1},\omega_4^{-2},\omega_4^{-3}\)
那么根据 DFT 能得到：
\(\omega_8^{0},\omega_8^{-1},\omega_8^{-2},\omega_8^{-3},\omega_8^{4},\omega_8^{3},\omega_8^{2},\omega_8^1\)
改造一下就是：
\(\omega_8^{0},\omega_8^{-1},\omega_8^{-2},\omega_8^{-3},\omega_8^{-4},\omega_8^{-5},\omega_8^{-6},\omega_8^{-7}\)
所以可以进行迭代。
至此，经过了四个神仙优化的锤炼后，理论部分终于完工。
代码部分
我们知道原理后，代码变得异常好写。
#include<bits/stdc++.h>
#define ld double
#define N 2000005
using namespace std;
const ld Pi=acos(-1);
int n,m;
struct CP{
ld x,y;
}f[N*2],g[N*2],tmp[N*2];
CP operator +(CP a,CP b){return (CP){a.x+b.x,a.y+b.y};}
CP operator -(CP a,CP b){return (CP){a.x-b.x,a.y-b.y};}
CP operator *(CP a,CP b){return (CP){a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x};}
void FFT(CP *f,int len,bool flag)
{
if(len==1) return;
CP *fl=f,*fr=f+len/2;
for(int i=0;i<len;i++) tmp[i]=f[i];
for(int i=0;i<len/2;i++)
fl[i]=tmp[(i<<1)],fr[i]=tmp[(i<<1)|1];
FFT(fl,len/2,flag),FFT(fr,len/2,flag);
CP cur=(CP){1,0},w=(CP){cos(2*Pi/len),(flag?1:-1)*sin(2*Pi/len)};
for(int i=0;i<len/2;i++)
{
tmp[i]=fl[i]+cur*fr[i];
tmp[i+len/2]=fl[i]-cur*fr[i];
cur=cur*w;
}
for(int i=0;i<len;i++) f[i]=tmp[i];
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<=n;i++) scanf("%lf",&f[i].x);
for(int i=0;i<=m;i++) scanf("%lf",&g[i].x);
for(m=n+m+1,n=1;n<m;n<<=1);
FFT(f,n,1);FFT(g,n,1);
for(int i=0;i<n;i++) f[i]=f[i]*g[i];
FFT(f,n,0);
for(int i=0;i<m;i++)
printf("%d ",(int)(f[i].x/n+0.5));
return 0;
}
虽然没超时，但是很慢。
其中 \(*f\) 是指向 \(f\) 数组的指针。\(f+x\) 可以取到 \(f\) 往后 \(x\) 位的指针。
接下来介绍迭代实现。
迭代实现
我们回到这个性质：
对于一个操作 \(\omega_n^k\)，它的左节点是 \(\omega_{2n}^k\)，右节点是 \(\omega_{2n}^{n+k}\)
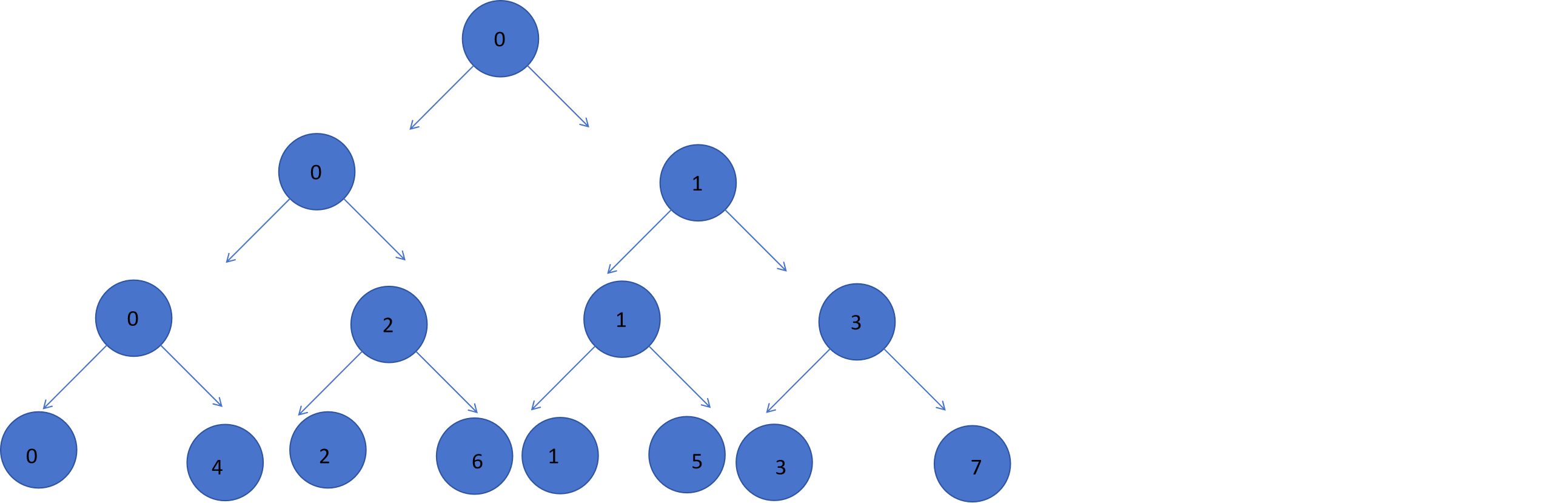
画的太屎了
我们可以发现，在第 \(x\) 层往右走，那么它会加上 \(2^x\)，往左则不变。
我们再仔细想想这个操作：
- 如果往左走，不变。
- 如果往右走，在最高位补 \(1\)。
我们分析最后一层第 \(6\) 个数(不算 \(0\))。
将 \(6\) 进行二进制拆分，显然是 \(110\)。
那么我们能分析它的行走规律：第 \(1\) 层右走，第 \(2\) 层右走，第 \(3\) 层左走。
所以它的值就是 \(2^0+2^1=3\)。
我们可以发现，每个数本质上就是当前的数翻转。
这个东西叫蝴蝶变换。
我们把最后一层的搞出来以后，往后的就直接搞就行了。
这样就把递归去了。
所以现在问题就是……
怎么快速求出一个数 \(x\) 的二进制翻转呢？
\(n\log n\) 固然可做，但是太慢了。
假设我们已经处理出 \(0\to x-1\)，怎么求 \(x\) 的翻转？
举个例子：
我们求 \((00110)1\) 的翻转。
我们已经知道了 \(0(00110)\) 的翻转。
所以我们先得到 \(0(00110)\) 的翻转：\((01100)0\)
我们知道，括号部分是我们想要的，我们右移一位就得到了。
最后判断第一位是不是 \(1\)，是的话在最高位补就 ok 了。
数列求完后，我们想想怎么改变原数组，我们知道开一个新数组是很浪费时间的。我们想要原地搞。
比如说，\(x\) 的翻转是 \(!x\) ，\(!x\) 的翻转就是 \(x\)。所以我们交换一下这两个位置的数就行了。
我们的迭代 FFT 火热出炉！
#include<bits/stdc++.h>
#define ld double
#define N 2000005
using namespace std;
const ld Pi=acos(-1);
int n,m;
int tr[N*2];
struct CP{
ld x,y;
}f[N*2],g[N*2];
CP operator +(CP a,CP b){return (CP){a.x+b.x,a.y+b.y};}
CP operator -(CP a,CP b){return (CP){a.x-b.x,a.y-b.y};}
CP operator *(CP a,CP b){return (CP){a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x};}
void FFT(CP *f,int n,bool flag)
{
for(int i=0;i<n;i++)
if(i<tr[i]) swap(f[i],f[tr[i]]);
for(int k=2;k<=n;k<<=1)
{
int len=(k>>1);
CP cur=(CP){1,0},w=(CP){cos(2*Pi/k),(flag?1:-1)*sin(2*Pi/k)};
for(int i=0;i<n;i+=k)
{
cur=(CP){1,0};
for(int j=i;j<i+len;j++)
{
CP tmp=cur*f[j+len];
f[j+len]=f[j]-tmp;
f[j]=f[j]+tmp;
cur=cur*w;
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<=n;i++) scanf("%lf",&f[i].x);
for(int i=0;i<=m;i++) scanf("%lf",&g[i].x);
for(m=n+m+1,n=1;n<m;n<<=1);
for(int i=0;i<n;i++) tr[i]=(tr[i>>1]>>1)|((i&1)?(n>>1):0);
FFT(f,n,1),FFT(g,n,1);
for(int i=0;i<n;i++) f[i]=f[i]*g[i];
FFT(f,n,0);
for(int i=0;i<m;i++) printf("%d ",(int)(f[i].x/n+0.5));
return 0;
}
所以差不多就结束了，这已经是最经典的 FFT 了。
附加：三次变两次 FFT
我们定义一个函数 \(T(x)\)，\(T(x)=F(x)+G(x)i\)。
然后给它平方一下。\(T(x)=F(x)^2-G(x)^2+2F(x)G(x)i\)
所以虚部就是我们想要的，这样两次就能搞了。
所以一般数满足的，多项式一般都有，这个时候多项式就产出来全家桶了。
