[dp 小计] SOSdp
复健 SOSdp(sum over subsets dynamic programming)。
引入
令 \(F(x)=\sum\limits_{u\subseteq x} A(u)\) 其中 \(A\) 为给定数组，求出 \(\forall x, F(x)\) 。
思路一
暴力枚举子集，时间复杂度 \(O(4^n)\)。
思路二
优化子集枚举，时间复杂度 \(O(3^n)\)。
思路三
考虑 SOSdp 。
考虑到每次求 \(F(x)\) 时都是重复暴力枚举，这一步会浪费很多时间，同时，我们会联想到 dp 的思想，利用上一次的结果加速转移。
如果按照普通状压 dp 的思想，如果我们从一个状态 \(mask\) 的所有子集转移而来，很明显会产生重复贡献，如果从单一状态转移过来，枚举其它状态时间复杂度只是一个 \(\frac{1}{2}\) 的常数，我们需要一种巧妙的 dp ，使每个贡献都是有效的，并且快速就能转移。
因此，我们设计一个新的状态：\(g[mask][i]\) ，表示在考虑前 \(i\) 位已经确定的情况下，\(mask\) 的子集和。注意这的前 \(i\) 位是二进制的前 \(i\) 位，是从小到大的。
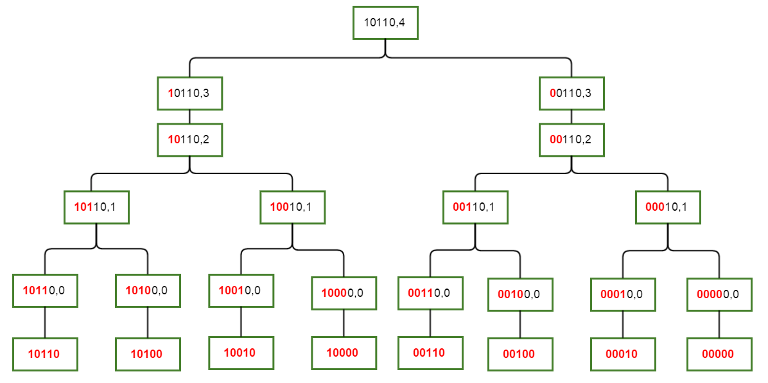
我们来看这个 codeforces blog 上的图。
其中，红色部分是摁死部分，这一部分不能变动，也没有计算子集贡献，黑色部分的子集和已经计算完毕，也就是说，我们任意取黑色部分的子集和红色部分的全集的并集已经计算完毕了。
这张图是十分的清晰易懂的。
举个例子 ， \(g[10010][1]=A(10000)+A(10010)\)
那么我们看图也知道怎么转移了。
注意这不是一棵树，是一个 DAG 。
为什么能做到不重不漏呢？因为我们加入了摁死红色部分的限制条件，因此分开的两个子问题是无交的。
这就很妙的解决了转移的问题。时间复杂度 \(O(n2^n)\)。
一种更通俗的理解就是，枚举每个 \(1\) 的位置，子问题就是不取当前的 \(1\) 和取当前的 \(1\) 。
一般的，子集 dp 都可以使用滚动数组优化，在草稿纸上推好柿子就行。
子集 dp 在优秀的时间复杂度内能处理复杂的子集问题。
for(int mask=0;mask<(1<<n);mask++) f[mask]=a[mask];
for(int i=1;i<=n;i++)
{
for(int mask=0;mask<(1<<n);mask++)
if(mask&(1<<i-1)) f[mask]+=f[mask^(1<<i-1)];
}
为什么正着枚举是正确的？
因为贡献的这一位在这一轮循环不会更新。
题目
有些很板的题套套容斥就能做，不讲了。
Subset
天才题。
问题是这样的：
\(3\) 个操作
- 增加一个数 \(x\)
- 删除一个数 \(x\)
- 求 \(x\) 的子集个数
\(Q\le2\times 10^5,x\le 2^{16}\)
我们想想怎么求单一个 \(mask\) 的子集和。
明显，朴素的算法就是 \(2^{bit}\) 枚举子集。但是这样过不了。
我们可以利用折半搜索的思想。
把一个数 \(x\) 拆成两部分，前 \(a\) 位和后 \(b\) 位。
我们预处理 \(x\) 的前 \(a\) 位，暴力把每个前 \(a\) 位的所有超集都预处理好。时间复杂度 \(O(2^a)\)。
对于后 \(b\) 位，相当于问后 \(b\) 位的子集和。这个你也可以直接爆搞，时间复杂度 \(O(2^b)\) 。
综上，时间复杂度位 \(O(Q(2^a+2^b))\) 。
这是怎么想到这种逆天思路的？
点击查看代码
#include<bits/stdc++.h>
#define ll long long
#define N 200005
#define M 16
#define cut 8
#define full 255
//using namespace std;
int q;
struct node{
int d[(1<<cut)+5];
inline void add(int x,int v){d[x]+=v;}
int ask(int x)
{
int sum=0;
for(int mask=x;;mask=x&(mask-1))
if(!mask) return sum+d[0];
else sum+=d[mask];
}
}b[(1<<cut)+5];
void updata(int x,int v)
{
int bit=(x>>cut),mask,num;
mask=num=full^bit;
while(1)
{
b[mask|bit].add(x&full,v);
if(!mask) return;
mask=(mask-1)#
}
}
int main()
{
scanf("%d",&q);
while(q--)
{
char opr;
int x;
scanf("%s%d",&opr,&x);
if(opr=='c') printf("%d\n",b[x>>cut].ask(x&full));
else updata(x,opr=='a'?1:-1);
}
return 0;
}
一些比较难的题（待补）
Jersey Number
题意：给出字符串，求两个区间字符交集不为空的个数。
思路：容斥
转为求区间交集为空个数。
然后有 \(O(n^2)\) 个区间，爆算肯定爆。
然后我们发现可以像扫描线那样快速处理区间。
然后就变成了经典问题，选两个数与起来为 \(0\) 。
Covering Sets
这个东西我们要用到一个新的东西：高维差分。
高维差分就是给出 \(mask\) 的子集和，倒推回 \(mask\) 的状态。
怎么倒推呢？
我们先举一个简单的例子：
\(\{101\}\Rightarrow \{101\},\{100\},\{001\},\{000\}\)
我们需要减去 \(\{100\},\{001\},\{000\}\) 这一坨东西。
好像很难办的样子，每次减掉有可能会重又有可能会漏。
我们可以借助 SOSdp 的思想。
定义 \(f[mask][i]\) 表示我们已经确定了前 \(i\) 位时候的子集和。
我们继续看这个图：
我们按死黑色部分，存储了红色部分的所有子集和。
我们看看怎么转移。
如果 \(mask\) 第 \(i\) 位是 \(0\) ，那么很明显，摁死这一位是没有意义的，也就是说这一位没有子集贡献，直接转移 \(f[mask][i]=f[mask][i-1]\) 即可。
否则，这一位就是又贡献的了。也就是说第 \(i\) 位是 \(1\) 的情况。
我们怎么得到第 \(i\) 位的贡献呢？
那么就是很简单的容斥，这一位所有子集的贡献减去不选这一位的贡献，也就是 \(f[mask]=f[mask][i+1]-f[mask\oplus 2^i][i+1]\) ，也就是我们要强制确定这一位选的数。
这个直接滚动数组碾过去就行。
回到这道题。
经典考虑贡献，对于这道题，就是一个很容易计算 \(mask\) 的和问题，对于单一贡献，套差分即可。
CF1679E
牛逼题。
一些经典拆贡献的做法就不解析了，现在我们直接转到问题最难的部分。
我们发现这个维护的东西是个指数。
答案是 \(mask\) 的位数然后乘上每个指数的答案。
你会发现这个指数太难维护了。
然后因为底数很小，直接枚举底数爆搞就行。天才！
时间复杂度 \(O(n^2+k^22^k)\)。
