LCA 算法 ： dfn 序

洛谷题解区那个题解马蜂让我读到自闭，这篇文章，详细的讲一讲这个算法。

一种基于预处理的快速 LCA 算法。
预处理需要 \(O(n\log n)\) 查询 ，\(O(1)\)，空间复杂度 \(O(n\log n)\)。

根据 dfn 序的性质，若 \(u\) 是 \(v\) 的祖先，那么 $dfn_u<dfn_v $，因为先遍历节点再遍历子树，所以 \(u\) 先会遍历到。
所以，我们知道，节点 \(u\) 的祖先存在 \(1\to dfn_u\) 这一段路径上。

所以，对于节点 \(u,v\) ，\(lca(u,v)\) 一定在 $1\to \min(dfn_u,dfn_v)$ 之间。
然而这样很难搞。因为我们不知道求出来的是不是 \(lca\) ，可能查到很高的祖先，甚至根节点。
所以我们考虑查询 \(lca\) 的儿子节点。

不妨设 \(dfn_u<dfn_v\) 我们思考怎么查询。
我们可以确定，\(dfn_u\to dfn_v\) 这一段是绝对不存在祖先节点的，因为最近公共祖先起码在 \(1\to dfn_u\) 这个范围内。

然后，根据 \(dfn\) 序的美妙性质，\(u\) 能遍历到 \(v\)，肯定往上跑到 \(lca\) 至少一次然后选择去了子树 \(v\) 。所以我们查询 \([dfn_u,dfn_v]\) 区间内 \(deep\) 最小值，就是 \(lca\) 儿子。可以理解为，这次走到的，就是 \(lca\to v\) 时链的第一个点。
这是在不同子树的情况，如果在相同子树，也就是说 \(lca=u\) ，那我们等价转化问题，查询 \([dfn_u+1,dfn_v]\) 不就行了吗。

然后对于情况 \(1\) ，\(dfn_u\) 肯定不是最小的。因为不同子树。

所以我们算法完成了：

点击查看代码

#include<bits/stdc++.h>
#define N 500005
#define ll long long
using namespace std;
int n,m,root;
int head[N],tot=1;
struct edge{
	int to,next;
}e[N*2];
void add(int u,int v)
{
	e[tot]=(edge){v,head[u]};
	head[u]=tot++;
}
int dfn[N],tim,dep[N];
int f[N][20],w[N],lg[N],fa[N];
void dfs(int now,int f)
{
	dep[now]=dep[f]+1;
	dfn[++tim]=now;
	w[now]=tim;
	fa[now]=f;
	for(int i=head[now];i;i=e[i].next)
	{
		int son=e[i].to;
		if(son==f) continue;
		dfs(son,now);
	}
}
int cmp(int u,int v){return dep[u]<dep[v]?u:v;}
int lca(int u,int v)
{
	if(u==v) return u;
	u=w[u],v=w[v];
	if(u>v) swap(u,v);
	++u;
	int len=lg[v-u+1];
	return fa[cmp(f[u][len],f[v-(1<<len)+1][len])];
}
int main()
{
	scanf("%d%d%d",&n,&m,&root);
	for(int i=1;i<n;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		add(u,v);
		add(v,u);
	}
	dfs(root,0);
	lg[0]=-1;
	for(int i=1;i<=n;i++) lg[i]=lg[i>>1]+1,f[i][0]=dfn[i];
	for(int i=n;i>=1;i--)
		for(int j=1;j<=lg[n-i+1];j++)
			f[i][j]=cmp(f[i][j-1],f[i+(1<<j-1)][j-1]);
	while(m--)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		printf("%d\n",lca(u,v));
	}
	return 0;
}

和题解那篇写的差不多，但是我觉得他数组压缩、压行太严重了。
便于理解，最后给出一个例子。

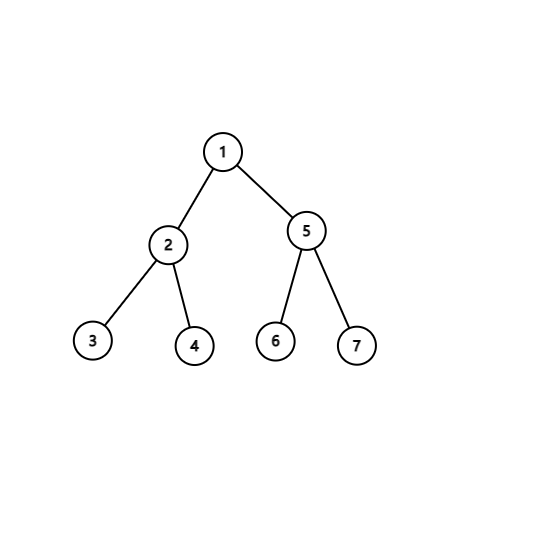
上面这棵树的其中之一 dfn 序为：
\(1,5,7,6,2,4,3\)
求解 \(4,7\) 的 \(lca\) ，很明显，经过了 \(2\) 这个点，这个点就是 \(lca\) 的儿子。
求解 \(4,5\) 的 \(lca\) ，很明显，经过了 \(2\) 这个点，这个点就是 \(lca\) 的儿子。
求解 \(4,3\) 的 \(lca\) ，很明显，经过了 \(3\) 这个点，这个点就是 \(lca\) 的儿子。

综上，我们只需要在对应区间内找到最小深度点即可。