2-SAT 小计

前置知识：
Tarjan ，SCC缩点。

引入

有一堆人要吃饭。
第一个人：
我想吃香精煎鱼，不想吃香菜逢仁鸡 。
第二个人：
我不想吃油饼，不想吃香精煎鱼。
第三个人：
我想吃油饼，也想吃香菜逢仁鸡。

你是厨师，你做的菜要满足上面所有人的口味两个的任意之一。
这怎么办？
这就是经典的 2-SAT 问题。

介绍

科学家证明了 n-SAT 问题中， \(n\ge 2\) 只能暴力做。
我们看看 \(n=2\) 怎么乱搞。

首先，可以把原问题抽象成布尔变量问题。
及 \(a_x=p\or a_y=q\)
我们想想这代表什么。
这意味着，当我不满足 \(a_x=p\) 时，我一定要满足 \(a_y=q\)
相反也是同理的。可以发现，这可以代表所有合理的情况。
不妨设计 \(2n\) 个点，\(x\) 点表示 \(x\) 取 \(1\) 的时候，\(x+n\) 点表示 \(x\) 取 \(0\) 的时候。
把 \(u\to v\) 链接一条有向边，表示取了 \(u\) 就必须取 \(v\)。
下图是一个例子。

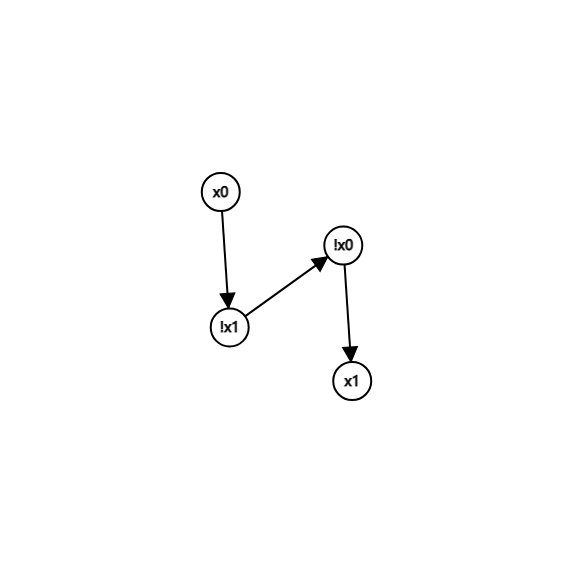
我们发现，我们可以根据图轻松的构造出一组合法的解。
那什么时候不合法呢？
我们发现，这是一个有向图，那么只要 \(x\) 取和 \(x\) 不取互相约束，就无解。
也就是这俩个点不能在一个 SCC 里面。
判断就很简单了。怎么构造方案呢？

我们知道，如果两个点取和不取都连一起了，那么我们选择后面取的那个，就是拓补序大的那个。
由于 Tarjan 算法算出来的染色就是逆拓扑序，所以判断哪个颜色小就是哪个。