算法笔记 Manacher

简单介绍

Manacher ，中文马拉车，是一种能在 \(O(n)\) 的时间内找到最长回文子串的优秀算法

问题引入

问题：给定字符串 \(s\) 求出 \(s\) 的最长回文子串并输出长度
\(|S|\le 10^7\)

思考

算法 \(1\)

我会暴力！
\(O(n^2)\) 枚举所有子串 ，\(O(n)\) 判断
时间复杂度 \(O(n^3)\)

算法 \(2\)

暴力太浪费时间
分析回文串的特质
容易发现 对于长度为奇数每个回文串 一定有一个对称中心
对于偶数 同理
因此我们 \(O(n)\) 枚举每个对称中心 暴力往两端拓展即可
鉴于分类讨论麻烦 我们在每个字符间插入特殊符号即可避免分类讨论


为了不越界判断 通常我们会在 \(s_0\) 这里插入一个与所有字符不一样的字符
这样做是为了判断超界 思考一下 不这样做 \(s_0\) 与 \(s_{n+1}\) 两个字符是相同的 这样会一直超界匹配下去

建串 code

void build()
{
	n=strlen(t+1);
	s[0]='>',s[1]='#';
	for(int i=1;i<=n;i++)
		s[i<<1]=t[i],s[(i<<1)|1]='#';
	n=(n<<1)|1;
}

其它算法

哈希 + 二分 ：判断用哈希和二分 时间复杂度 \(O(n\log n)\)
哈希 + 答案单调：不断扩展 时间复杂度为大常数 \(O(n)\)

马拉车

马拉车是一个神奇的算法 它能在看似 \(O(n^2)\) 的复杂度做到 \(O(n)\) 处理
时间复杂度浪费在多次判断字符串相等
因此 引入一个变量 \(mr\) 和 \(mid\) 表示过程到的最右边于中点

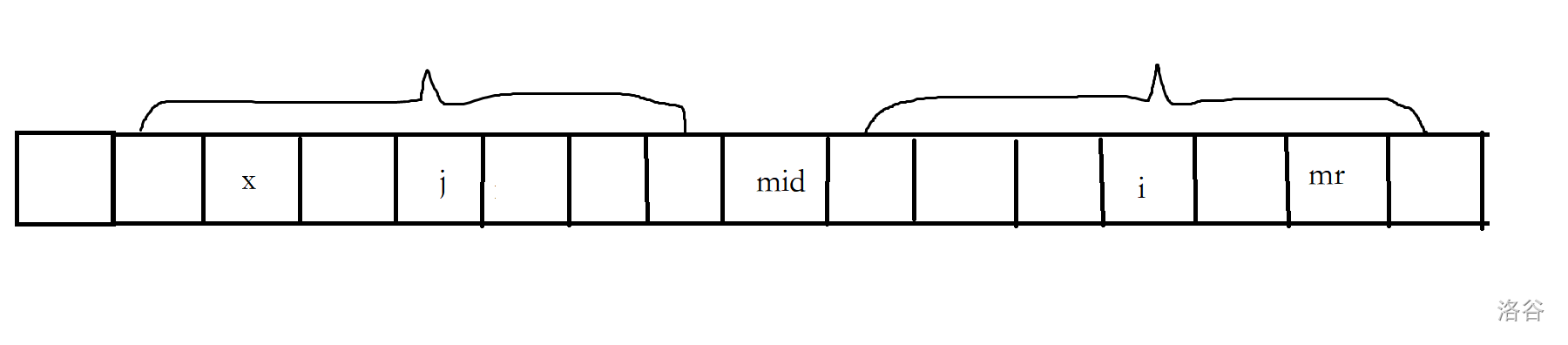
如图 对称区间为 \(x\to mr\)
假如 \(i\) 在 \(mid\to mr\) 之间
那么 我们可以借助 \(i\) 的对称点 \(j\) 快速更新答案
但是又不能超过 \(x\) 左边 因为左边并不能保证对称的性质
所以可以预处理为 \(p_i=\min(p_j,mr-i+1)\)
预处理完后进行暴力扩展
对于 \(j\) 的计算 使用中点公式即可
\(\because (i+j)/2=mid\therefore j=mid\times 2-i\)
对于不在区间内的 直接暴力扩展即可

code

#include<bits/stdc++.h>
#define N 22000005
using namespace std;
int n,cnt;
char t[N],s[N];
void build()
{
	n=strlen(t+1);
	s[0]='>',s[1]='#';
	for(int i=1;i<=n;i++)
		s[i<<1]=t[i],s[(i<<1)|1]='#';
	n=(n<<1)|1;
}
int ans;
int mr,mid;
int p[N];
void solve()
{
	for(int i=1;i<=n;i++)
	{
		if(i<=mr) p[i]=min(p[mid*2-i],mr-i+1);
		while(s[i-p[i]]==s[i+p[i]]) p[i]++;
		if(i+p[i]>mr) mr=i+p[i]-1,mid=i;
		ans=max(ans,p[i]-1);
	}
}
int main()
{
	scanf("%s",t+1);
	build();
	solve();
	printf("%d",ans);
	return 0;
}

关于时间复杂度

不会证明
感性理解 \(mr\) 是递增的