后缀数组小计
0 前言
被迫上班了属于是
前置知识
- 倍增
- 基数排序
基数排序
这个很好理解
举个例子 : 对 \(n\) 对二元组 \((x,y)\) 排序 优先比较关键字 \(x\) 相同再比较关键字 \(y\)
第一步:以 \(y\) 为基准 从小到大把所有二元组排序 得到 \(y\) 递增的序列
第二部:以 \(x\) 为基准 从小到大把所有二元组排序 得到 \(x\) 递增的序列
因为保证原数列顺序不变 在 \(x\) 递增的同时 \(y\) 也是递增的 排序完毕
令值域为 \(w\) 时间复杂度为 \(O(w)\)
举个例子:
原 : \((3,4)\space (3,1)\space (1,5)\space (2,4)\)
第一次排序 : \((3,1)\space (3,4)\space (2,4)\space (1,5)\)
第二次排序 : \((1,5)\space (2,4)\space (3,1)\space (3,4)\)
听起来很简单 但是代码可不简单
#include<bits/stdc++.h>
#define N 10000005
#define M 1000005
using namespace std;
int n,a[N],b[N];
int cnt[N],sa[N],lsa[N];
int m,seed;
long long ans;
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
cin>>a[i]>>b[i];
for(int i=1;i<=n;i++) cnt[b[i]]++;
for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1];
for(int i=1;i<=n;i++) lsa[cnt[b[i]]--]=i;//第 16 行
//----------------------------
memset(cnt,0,sizeof cnt);
for(int i=1;i<=n;i++) cnt[a[i]]++;
for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1];
for(int i=n;i>=1;i--) sa[cnt[a[lsa[i]]]--]=lsa[i];//第 20 行
for(int i=1;i<=n;i++)
cout<<sa[i]<<"\n";
return 0;
}
来分析一下代码 先看分割线上的部分一:按第二关键字排序
- step \(1\) .记录下 \(y\) 出现次数
- step \(2\) .记录前缀和(废话)
- step \(3\) .得到排名
举个例子 :
\((1,4),(2,3),(1,3),(2,2),(3,1)\)
处理后得到的 \(cnt\) 数组:\(1,1,2,1\)
前缀和:\(1,2,4,5\)
我们惊奇的发现 第二关键字的顺序已经确定了
\(y=1\) 为 \(1\to 1\)
\(y=2\) 为 \(2\to 2\)
\(y=3\) 为 \(3\to 4\)
\(y=4\) 为 \(5\to 5\)
任意的,对于 \(y=x\) 在排列中的位置不就是 \(cnt_{x-1}+1\to cnt_x\) 吗!
如第 \(16\) 行 第二关键字的放入不需要任何顺序 直接按顺序放入即可
现在来到第二部分 同第一部分思想一样 这次处理的是第一关键字
如第 \(20\) 行 这次放入就有顺序了 我们按照处理完第二关键字的次序从后往前放入
为什么?因为我们能保证第一关键字有序的同时要保证第二关键字有序
因此 因为填数是从后往前填的 所以应该先填第二关键字大的
第一次处理出了从小到大的第一关键字 所以要反着遍历
1 基本概念
我们规定如下的数组:
- \(rk[i]\) 表示开头下标为 \(i\) 的后缀的排名
- \(sa[i]\) 即常说的后缀数组 表示排名为 \(i\) 的后缀开头下标
显然 有性质 \(sa[rk[i]]=rk[sa[i]]=i\)
理解一下:
对于 \(sa[rk[i]]=i\) 表示取出第 \(i\) 个后缀的排名 再引用该排名的位置即 \(i\)
对于 \(rk[sa[i]]=i\) 表示取出排名为 \(i\) 的后缀的位置 再求出该位置的排名即 \(i\)
(OI wiki 的图)
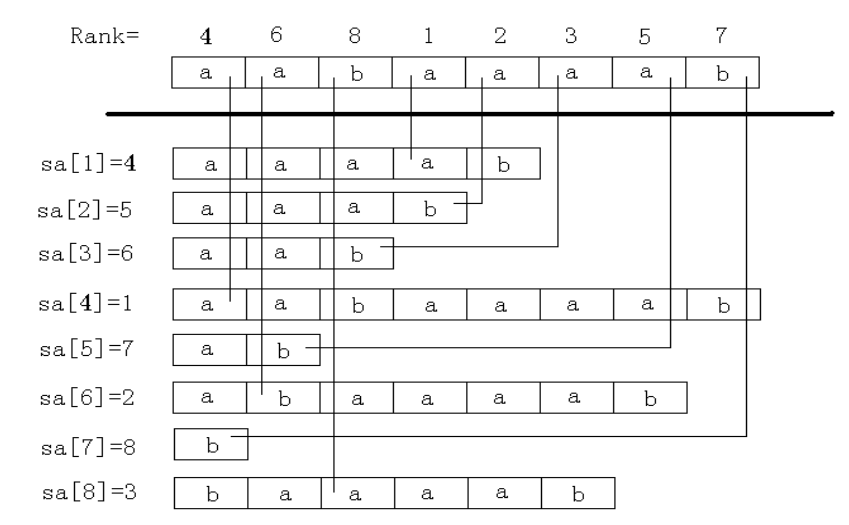
2 后缀数组求法
不难发现 只需要求出 \(rk\) 数组 \(sa\) 数组自然就能求出
1.\(O(n^2\log n)\)
这个肯定自己想都能想出来
先 \(O(n)\) 枚举所有后缀 然后使用快排
因为字符串比较时间是 \(O(n)\) 的 因此总的时间复杂度是\(O(n\times n\log n)\) 即 \(O(n^2\log n)\)
2.\(O(n\log^2 n)\)
我们发现时间瓶颈 \(n\) 卡在了 \(O(n)\) 的比较上
我们想想怎么优化排序 于是倍增法就出来了
主要思想就是一部分 一部分粘合
(OI wiki)
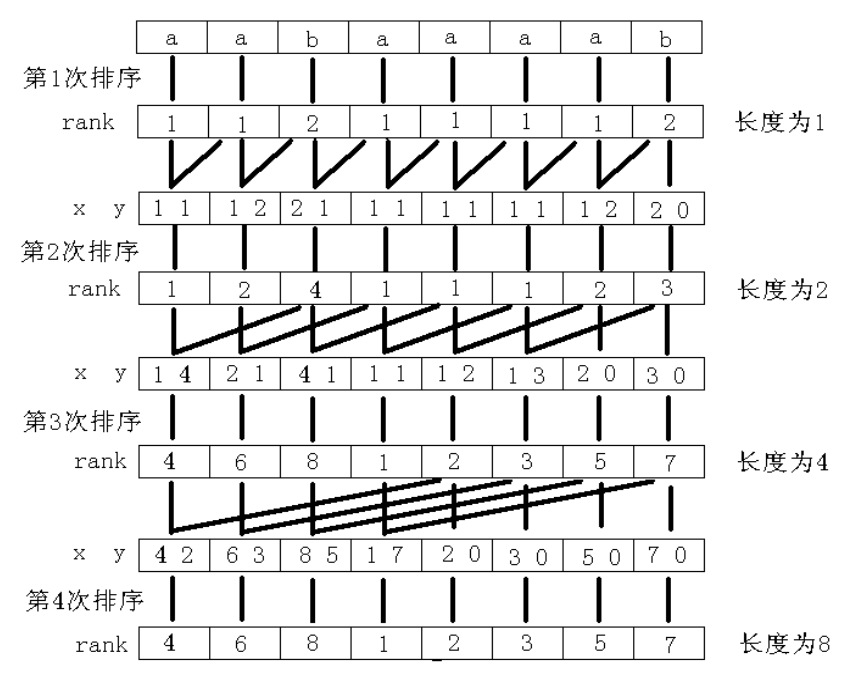
这一部分很好理解
以 最长的后缀 (下标从 \(1\) 开始为例)
首先 得到单个字母的 \(rank\) 值 (第一步)
然后 求出子串 \([1\to 2]\) 当前的 \(rank\)
怎么求?很好理解 记录第一关键字 \(x=rk1\) 第二关键字 \(y=rk2\)
排序所有的 \((x,y)\) 二元组可以得到所有当前的后缀排名
这时 会发现最后一位已经无法向后拓展了 (即第二次排序时最后的第二关键字)
那么 这时 记这位为 \(0\)
思考一下 这样 就与字符串比较的规则相符了
然后 同理 第三次求出子串 \([1\to 4]\)
第四次求出子串 \([1\to 8]\)
这样 不难发现 当所有的数第二关键字为 \(0\) 时 此时便得到了所有后缀
此时 第一关键字便是 \(sa\) 数组
非常巧妙的方法 这样 将比较是时间复杂度缩短为常数级别
现在分析时间复杂度
不难发现 倍增的次数为 \(O(\log n)\)
每次使用快排 时间复杂度 \(O(n\log n)\)
总体时间复杂度 \(O(n\log^2 n)\)
别看理论简单 代码却很抽象
#include<bits/stdc++.h>
#define N 1000005
using namespace std;
char s[N];
int n;
int sa[N],rk[N*2],lrk[N*2];
int k;
bool cmp(int a,int b)
{
return rk[a]^rk[b]?rk[a]<rk[b]:rk[a+k]<rk[b+k];//先以第一关键字排序 再以第二关键字排序
}
int main()
{
scanf("%s",s+1);
n=strlen(s+1);
for(int i=1;i<=n;i++) sa[i]=i,rk[i]=s[i];//初始化 将第一次排名处理好 存入未排序的sa数组
for(k=1;k<n;k<<=1)
{
sort(sa+1,sa+1+n,cmp);//算出当前子串数组的sa 下面的步骤就是用sa推rk
memcpy(lrk,rk,sizeof rk);//复制一份rk数组
int p=0;
for(int i=1;i<=n;i++)
if(lrk[sa[i]]==lrk[sa[i-1]]&&lrk[sa[i]+k]==lrk[sa[i-1]+k])
rk[sa[i]]=p;//枚举排名 i 比较与上一个拼接是否相同 相同就不是增大的排名
else rk[sa[i]]=++p;
}
for(int i=1;i<=n;i++) printf("%d ",sa[i]);
return 0;
}
注意几个细节 \(k\) 是全局变量 否则无法参加 cmp 函数的计算
理解难点在于用 \(sa\) 推 \(rk\)
以求 \(rk_2\) 为例
- step \(1\) 通过 \(sa\) 数组取出在新 \(rk\) 中排名为 \(1\space 2\) 的位置
- step \(2\) 比较在旧 \(rk\) 中排名为 \(1\space 2\) 时的拼接是否相同
- step \(3\) 如果有效 在新 \(rk\) 中 排名为 \(1\space 2\) 位置的值
3.\(O(n\log n)\)
非常简单的优化
容易发现 瓶颈在于快排
发现有 \(x,y\le n\) 的性质
双关键字排序将快排换为基数排序即可
注意一开始的 \(x,y\le 122\) \((z=122)\)
code
#include<bits/stdc++.h>
#define N 1000005
using namespace std;
char s[N];
int n,m=128;
int lsa[N],sa[N],rk[N*2],lrk[N*2],cnt[N];
int k;
void Qsort()
{
memset(cnt,0,sizeof cnt);
for(int i=1;i<=n;i++) cnt[rk[i+k]]++;
for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1];
for(int i=1;i<=n;i++) lsa[cnt[rk[i+k]]--]=i;
memset(cnt,0,sizeof cnt);
for(int i=1;i<=n;i++) cnt[rk[i]]++;
for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1];
for(int i=n;i>=1;i--) sa[cnt[rk[lsa[i]]]--]=lsa[i];
return;
}
int main()
{
scanf("%s",s+1);
n=strlen(s+1);
for(int i=1;i<=n;i++) sa[i]=i,rk[i]=s[i];
for(k=1;k<n;k<<=1)
{
Qsort();m=n;
memcpy(lrk,rk,sizeof rk);
int p=0;
for(int i=1;i<=n;i++)
if(lrk[sa[i]]==lrk[sa[i-1]]&&lrk[sa[i]+k]==lrk[sa[i-1]+k])
rk[sa[i]]=p;
else rk[sa[i]]=++p;
}
for(int i=1;i<=n;i++) printf("%d ",sa[i]);
return 0;
}
理论结束 建议两种代码都写一次
3 后缀数组基础应用
这里的应用只需要知晓后缀数组的本质因素
1.前后缀大小比较
例题:here
思考:
很明显,破环为链
直接把 \(s\) 复制一遍粘到后面去
由于题目求的只是该循环最后一个字符 因此 直接求出后缀数组即可
举个例子:
\(\text{abcda}\to \text{abcdaabcda}\)
可以发现 我们已经把要求的循环串都变成了某一后缀的固定长度前缀 且只需要到最后一个字符
这样 比较后缀数组即可
比如 \(\text{abcdaabcda} , \text{aabcda}\)
当比较了前 \(5\) 位时 会取第 \(5\) 位字母 后面的字串没有意义
练习 : P2870
补充:当同时比较前后缀大小时 需要在字符串末尾插入一个极小数 这样 长度比较小的后缀才会小于长度比较长的前缀
2.在线求文本串中的模式串
例题:here
只需要做到 52pts 即可
思考:当我们求出 sa 以后 所有的后缀大小已经确定
那么 每个模式串一定是某个后缀的前缀
既然后缀已经排好序了 那我们直接在后缀中找这个前缀即可
因为每个后缀开始位置不同 因此只要有一个后缀前缀于模式串相同便有 \(1\) 的贡献
令当前模式串为 \(T\) 比较字符串的时间复杂度是 \(O(|T|)\) 的 因此总的时间复杂度是 \(O(|S|+|T|\log|S|)\)
虽然没有 AC 自动机的 \(O(|S|+|T|)\) 优秀 但是优点在于它是一个在线算法
核心 code
int cmp(string t,int pos)
{
if(n-pos+1<t.size()) return t<s.substr(pos,n-pos+1);
if(t==s.substr(pos,t.size())) return 2;
return t<s.substr(pos,t.size());
}
int query(string s,bool k)//k=1 为最右边
{
int l=1,r=n;
while(l<=r)
{
int mid=(l+r)/2;
if(cmp(s,sa[mid])==2)
{
if(k) l=mid+1;
else r=mid-1;
continue;
}
if(cmp(s,sa[mid])) r=mid-1;
else l=mid+1;
}
if(k) return l-1;
else return r+1;
}
4 \(height\) 数组
学 sa 不学 height 相当于白学
\(99\)% 的 sa 题目都与 height 有关
我们给出如下定义:
- \(lcp(x,y)\)
\(lcp(x,y)\) 为字符串 \(x\) 与 \(y\) 的最长公共前缀的长度
举个例子 , \(acdefb\) 与 \(acfdae\) 的最长公共前缀长度是 \(2\space (ac)\) - \(height\) 数组
令 \(height_1=0 , height_i=lcp(sa_i,sa_{i-1})\) 即第 \(i\) 名后缀与 \(i-1\) 名后缀的 \(lcp\)
(网图)
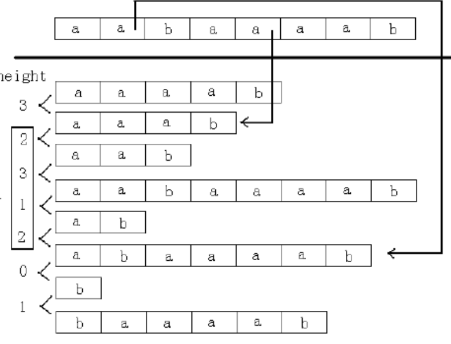
左边一列即为 \(height\) 数组
- \(H\) 数组
令 \(H_i=height[rk[i]]\) 即第 \(i\) 位后缀与它前一名后缀的 \(lcp\)
如上图 \(H=\{3,2,1,0,3,2,1,0\}\)
性质:
1. \(H_i\ge H_{i-1}-1\)
证明:
当 \(H_{i-1}\le1\) 性质显然成立
当 \(H_{i-1}>1\) 时,不难理解
不妨令第 \(i-1\) 位后缀为 \(s_1\) 它前一名为 \(s_2\)
第 \(i\) 位后缀为 \(t_1\) 它前一名为 \(t_2\)
我们知道 \(s_1=c+t_1\) 其中 \(c\) 为某个字符
从 \(s_1\) 到 \(t_1\) 相当于在开头去掉 \(c\)
那么 去掉 \(s_2\) 的开头字符一定有 \(H_{i-1}-1\) 的贡献
我们知道 后缀排好序后一定是从小到大的
根据此性质 容易得到 \(H_i\ge H_{i-1}-1\)
2.\(lcp(i,j)=lcp(j,i)\)
3.\(lcp(i,i)=len[i]=n-sa[i]+1\)
这两条性质显然
4.LCP Lemma
LCP Lemma : 对于任意 \(1\le i<j<k\le n\) 有 \(lcp(i,k)=\min(lcp(i,j),lcp(j,k))\)
证明:首先,令 \(\min(lcp(i,j),lcp(j,k))=p\)
因为 \(i,j\) 前 \(p\) 个字符相同 \(j,k\) 前 \(p\) 个字符相同
所以 \(i,k\) 前 \(p\) 个字符相同
现在证明 \(lcp(i,k)\le p\) 假设 \(lcp(i,k)>p\)
令 \(i,j,k\) 对应字符串为 \(u,v,w\)
钦定 \(lcp(i,j)=p\)
那么 根据假设 \(u[p+1]=w[p+1]\) 且 \(u[p+1]\ne v[p+1]\)
根据 \(i,j,k\) 在 sa 数组中 前 \(p\) 位相同
得到 \(u[p+1]\le v[p+1]\le w[p+1]\)
所以 \(u[p+1]=v[p+1]=w[p+1]\) 与条件矛盾
同理 对于 \(lcp(j,k)\) 自证不难
对于 \(lcp(i,j)=\min(lcp(i,j),lcp(j,k)\) 成立
5.LCP Theorem
LCP Theorem : 对于 \(i<j\) 有 \(lcp(i,j)=\min(height_{i+1}\to height_j)\)
证明:
\(\\min(height_{i+1}\to height_j)=min(lcp(k-1,k))\space (i+1\le k\le j)\)
由 LCP Lemma 可得
\(lcp(i,j)\)
\(=\min(lcp(i,i+1),lcp(i+1,j))\)
\(=min(lcp(i,i+1),lcp(i+1,i+2),lcp(i+2,j))\)
同理 经过归纳易证
\(height\) 的求法
根据性质 \(1\) 暴力求即可
code
void gethei()
{
int k=0;
for(int i=1;i<=n;i++)
{
if(k) k--;
while(s[i+k]==s[sa[rk[i]-1]+k]) ++k;
hei[rk[i]]=k;
}
}
根据性质 \(H_i\ge H_{i-1}-1\)
\(k\le n\),\(k\) 只会减 \(n\) 次 ,加 \(2n\) 次 因此时间是 \(O(n)\) 的
5 \(height\) 数组的应用
1 子串的 \(lcp\)
由于每个子串都是某个后缀的前缀 只需要计算两个后缀的 \(lcp\) 稍加处理即可
2 子串的大小
假设比较 \(S[a...b]\) 与 \(S[c...d]\)
计算 \(lcp(a,c)=p\) 若 \(p\ge \min(|A|,|B|)\) 就比较 \(|A|,|B|\) 即可
否则 比较 \(rk_a\) 与 \(rk_c\) 即可
3 不同子串数目
根据 不同子串数目 \(=\) 总子串数目 \(-\) 相同子串数目
因为子串为后缀前缀 相同子串即为最大公共前缀
因此 原式 = \(\frac{n(n+1)}{2}-\sum\limits_{i=1}^nheight_i\)
按照后缀排序的顺序枚举 每次新增的子串都是以其为开头的 因为 \(lcp\) 部分已经算过 不能重复计算
为什么不用算前面的?实际上,对于 \(i\) 我们取的是 \(max(lcp(1,i),lcp(2,i),lcp(3,i)...)\)
明显 \(lcp(i-1,i)\) 有最大值 即 \(height_i\) 得证
\(height\) 数组有很多灵活的运用 上面只是部分 还需多做题巩固!

