模拟套题 12.9
不敢想象这是曾经初二的人做的
T1 非皇后
大意:给定 \(R\) 行 \(C\) 列的 棋盘 你可以随便在一个格子放一个非皇后 要求不能走直线和对角线 走 \(M\) 步
将走过的格子按顺序记起来 求最终有多少种不同排列
Solution
dp 裸题
定义 \(f_{i,j,k}\) 为走了 \(i\) 次 ,到格子 \((j,k)\) 的方案
容易有转移 $f_{i,j,k}=\sum\limits f_{i-1,x,y} \space $
其中 \(x,y\) 不是同行同列不是对角线
用四个前缀和优化一下就好了
时间复杂度 \(O(RCM)\)
T2 染色
给出 \(n\) 个结点 \(m\) 条边的无向图。有k种不同的颜色,编号 \(1\) 至 \(k\) 。现在你要对这n个结点染色,每个结点只能染一种颜色。还有一个特殊要求:凡是有边相连的两个结点,它们的颜色编号的和不能等于 \(z\) 。问有多少种不同的染色方案
\(n,m\leq 18\space k\leq 10^9\)
Solution
正面思考非常麻烦 看到 \(n,m\le 18\) 那肯定和 \(2^n\) 脱不了关系
颜色很大 不能装压 还有 \(2^n\) 次方的算法还有枚举 和 容斥
显然 可以容斥
直接枚举不满足的边 然后分类讨论即可
用并查集维护 时间复杂度是 \(O((n+m)2^m\log n)\) 并查集常数很小 可以接受
最大是 993ms
T3 子序列整数
给定字符串 \(S\) 和整数 \(n\)
求出有多少个不同的 \(S\) 的子序列 \(P\) 使得 \(n|P\)
\(|S|\le 5000\space n\le1000\)
Solution
难度还行
考虑难度在于 不同的 子序列
要是没有这个条件 一个 dp 划过去即可 时间复杂度 \(O(n^2|S|)\)
怎样才能保证每次产生的都是不同的呢?
我们要保证 每个数只记最开始出现的一次
根据这个,每个数的开头都是固定的了 注意 \(0\) 不能开头
这个时候手玩样例是最佳选择
\(Instance:\)
\(12412412\)
\(1\)
\(2,12\)
\(4,14,24,124\)
\(11,21,121,41,141,241,1241\)
\(22,12,42,142,242,1242,112,212,121,412,1412,2412,12412\)
\(...\)
一手玩玩 规律马上就出来了
能往下接的必须从上一个相同的数开始
记一下 \(last_{num}\) 即可
分析时间复杂度
\(O(n^2|S|) \to O(n|S|)\) 有常数 \(10\)
因为每个点的转移都是一部分 所以时间复杂度大大降低
均摊一下就有了
T4 三角形
前置芝士:This
想了三天才做出来 用了挺多数学课是时间推 同机房的 Sktn0089 大神 30min 就切了 而且方法快多了
很毒瘤的一道题

第一步肯定是手玩样例
手玩一下 不难发现合理的只有两种情况
- 1.在目前已经围成的三角形内部 此时随便连都是三个
- 2.在目前围成的三角形延长线的里面 这样会扩大三角形的面积
最后成的三角形的外围是固定的
我们可以这样拆分一个排列:
\([P_1,P_2,P_3],P_4,[P_5],P_6,P_7,[P_8],···,[P_n]\)
其中 有括号的表示 三角形 的坐标发生改变
这样 每种排列都有一个唯一的跳跃
我们用一个状态来记录这些排列:\(f_{i,j,k}\) 表示第 \(i,j,k\) 个点构成了三角形
这样似乎就可 dp 转移了
但这是错的 我们的想法是转移维护三角形的扩大(情况1) 可是 这样无法维护情况 \(2\)
往三角形内部一放 可能就不是排列了
怎么办?
为此 我们再加一维 \(t\) 表示三角形内部的点
这样 每个排列就被我们表示出来了 因为三角形内部的是任意的 可以计做一维
这样 我们的 dp 就出来了
对于情况 \(1\) 有 \(f(i,j,k,t)+=f(i,j,k+1,t)\times k\)
对于情况 \(2\) 判断 \((i,j,k)\) 外面的点 \(x\) 能把这个图连成三角 \((i,j,x)\) 有\(f_{i,j,k,t}+=f_{i,j,x,P}\)
\(P\) 的处理后面会讲
最终的答案就是 \(f_{p1,p2,p3,0}\) 其中 \(p1,p2,p3\) 是最终的顶点
现在主要问题处理完了 下面就是细节
- 怎么判断一个点在不在三角形内部?
\(Solution\)
用最简单的方法 面积法
对于三角形内任意一点 \(P\) 有 \(S_{\Delta ABC}=S_{\Delta ABP}+S_{\Delta APC}+S_{\Delta PBC}\)
其中 对于 \(S_{\Delta ABC}=\frac{1}{2}\times |A_x\times B_y+B_x\times C_y+C_x\times A_y-A_y\times B_x-B_y\times C_x-C_y\times A_x|\)
- 怎么判断一个点在这个三角形外围能成三角?
这个是整道题最难的地方
经过大量列举分类 有两种思路
- 1 斜率
求出三种斜率 讨论即可
分类太大 作死了没做出来
- 2 交点
我觉得这是最好的方法
枚举这个点连接三角形的顶点
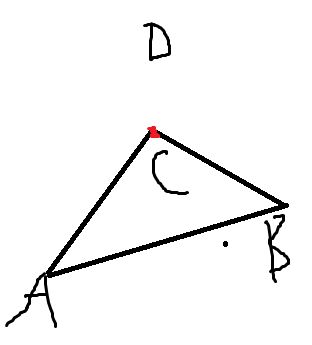
图上 C D 就是顶点 D 在 A B 延长线之间
怎么判断?
与其判断一个点在两条线之间 不如判断两个点在一条线两侧 即 A B 在 CD 两侧
这个用解析式做出交点判断即可 同时 C D 在交点同侧
通过推理一大坨方程就可以了
注意这里还有两个分类 就是他们 y 相同的情况
注意是不能 dp 的 因为我们无法处理点
Code
T1
#include<bits/stdc++.h>
#define N 205
#define ll long long
using namespace std;
int n,m,w;
const ll mod=(1e9)+7;
ll f[N][N][N],h[N],l[N],a[N*2],b[N*2],sum=1;
void add(ll &a,ll b)
{
a=(a+b)%mod;
}
int main()
{
scanf("%d%d%d",&n,&m,&w);
for(int k=1;k<=w+1;k++)
{
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
f[k][i][j]=(sum-h[i]-l[j]-a[i+j]-b[i-j+m]+f[k-1][i][j]*3)%mod;
sum=0;
memset(h,0,sizeof(h));
memset(l,0,sizeof(l));
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
ll v=f[k][i][j];
add(sum,v);
add(h[i],v);
add(l[j],v);
add(a[i+j],v);
add(b[i-j+m],v);
}
}
printf("%lld",(sum+mod)%mod);
return 0;
}
T2
#include<bits/stdc++.h>
#define N 25
#define ll long long
using namespace std;
const ll mod=1000000007;
int n,m;
ll k,z,ans,sum;
vector <int> E[N];
int vis[N],val[N];
int u[N],v[N];
int fa[N],w[N];
int find(int x)
{
return fa[x]^x?fa[x]=find(fa[x]):x;
}
void merges(int x,int y)
{
fa[find(x)]=find(y);
}
void dfs(int x,int v)
{
if(val[x]!=0)
{
if(val[x]!=v) w[find(x)]=1;
return ;
}
val[x]=v;
for(int i=0;i<E[x].size();i++)
{
int to=E[x][i];
dfs(to,-v);
}
}
void init()
{
for(int i=1;i<=n;i++)
{
fa[i]=i;
w[i]=val[i]=vis[i]=0;
E[i].clear();
}
}
int main()
{
scanf("%d%d%lld%lld",&n,&m,&k,&z);
for(int i=1;i<=m;i++)
scanf("%d%d",&u[i],&v[i]);
for(int i=0;i<(1<<m);i++)
{
init();
int cnt=0;
sum=1;
for(int j=1;j<=m;j++)
if(i&(1<<j-1))
{
cnt++;
vis[u[j]]=vis[v[j]]=1;
E[u[j]].push_back(v[j]);
E[v[j]].push_back(u[j]);
merges(u[j],v[j]);
}
for(int j=1;j<=n;j++)
if(!val[j]&&vis[j]) dfs(j,1);
for(int j=1;j<=n;j++)
if(!vis[j]) sum=sum*k%mod;
else
{
if(j!=find(j)) continue;
if(w[j])
if(!(z&1)&&k>=z/2) ;
else sum=0;
else
sum=sum*max(0ll,min(k,z-1)-max(z-k,1ll)+1)%mod;
}
if(cnt&1) ans=(ans-sum)%mod,ans=(ans+mod)%mod;
else ans=(ans+sum)%mod;
}
printf("%lld",ans);
return 0;
}
T3
#include<bits/stdc++.h>
#define N 5005
#define ll long long
using namespace std;
const ll mod=1000000007;
int n,lst[15],len,vis[15];
char s[N];
ll f[N][1005],ans;
int main()
{
scanf("%d%s",&n,&s);
len=strlen(s);
for(int i=1;i<=len;i++)
{
int x=s[i-1]-'0';
if(vis[x]||x==0) continue;
vis[x]=1;
f[i][x%n]=1;
}
for(int i=0;i<=9;i++) lst[i]=1;
for(int i=1;i<=len;i++)
{
int x=s[i-1]-'0';
for(int j=lst[x];j<=i-1;j++)
{
for(int k=0;k<n;k++)
f[i][(k*10+x)%n]+=f[j][k],
f[i][(k*10+x)%n]%=mod;
}
lst[x]=i;
ans=(ans+f[i][0])%mod;
// for(int k=0;k<n;k++) cout<<f[i][k]<<" ";
// cout<<"\n";
}
printf("%lld",ans);
return 0;
}
/*
24 1020402
1
10
12
2
102
12120
1
2
12
11
21
121
22
122
112
212
1212
*/
T4
#include<bits/stdc++.h>
#define N 45
#define ll long long
#define ld long double
using namespace std;
int n;
ll f[N][N][N][N];
int Ct[N][N][N];
const ll mod=(1e9)+7;
ll A[N],ans;
struct point{
int x,y;
}a[N];
int S(point a,point b,point c)
{
return abs(a.x*b.y+b.x*c.y+c.x*a.y-a.y*b.x-b.y*c.x-c.y*a.x);
}
int In(point x,point y,point z,point q)
{
return S(x,y,q)+S(x,z,q)+S(y,z,q)==S(x,y,z);
}
ld slope(point a,point b)
{
return 1.0*(a.y-b.y)/(a.x-b.x);
}
bool checks(point a,point b,point c,point x)
{
if(a.x==b.x&&c.x==x.x) return 0;
ld k1,k2,b1,b2,crosx,crosy;
if(a.x==b.x)
{
k1=slope(c,x),b1=c.y-k1*c.x;
crosx=a.x,crosy=k1*crosx+b1;
}
else if(c.x==x.x)
{
k2=slope(a,b),b2=a.y-k2*a.x;
crosx=c.x,crosy=k2*crosx+b2;
}
else
{
k1=slope(c,x),k2=slope(a,b);
b1=c.y-k1*c.x,b2=a.y-k2*a.x;
crosx=1.0*(b2-b1)/(k1-k2),crosy=k1*crosx+b1;
}
return ((crosx>=a.x&&crosx<=b.x)||(crosx>=b.x&&crosx<=a.x)) && ((crosy>=c.y&&crosy>=x.y)||(crosy<=c.y&&crosy<=x.y));
}
bool check(point a,point b,point c,point x)
{
return checks(a,b,c,x)|checks(a,c,b,x)|
checks(b,a,c,x)|checks(b,c,a,x)|
checks(c,a,b,x)|checks(c,b,a,x);
}
ll dfs(int x,int y,int z,int t)
{
if(t<0) return 0;
if(f[x][y][z][t]!=-1) return f[x][y][z][t];
f[x][y][z][t]=0;
f[x][y][z][t]+=1ll*dfs(x,y,z,t+1)*(t+1)%mod;
f[x][y][z][t]%=mod;
for(int i=1;i<=n;i++)
if(x!=i&&y!=i&&z!=i&&In(a[x],a[y],a[z],a[i]))
{
if(check(a[x],a[y],a[i],a[z])) f[x][y][z][t]+=dfs(x,y,i,t-(Ct[x][y][z]-Ct[x][y][i]-1));
if(check(a[x],a[z],a[i],a[y])) f[x][y][z][t]+=dfs(x,z,i,t-(Ct[x][y][z]-Ct[x][z][i]-1));
if(check(a[z],a[y],a[i],a[x])) f[x][y][z][t]+=dfs(y,z,i,t-(Ct[x][y][z]-Ct[z][y][i]-1));
f[x][y][z][t]%=mod;
}
// cout<<x<<" "<<y<<" "<<z<<" "<<t<<" "<<f[x][y][z][t]<<"\n";
return f[x][y][z][t];
}
int main()
{
scanf("%d",&n);
A[0]=1;
for(int i=1;i<=n;i++)
scanf("%d%d",&a[i].x,&a[i].y);
memset(f,-1,sizeof(f));
for(int x=1;x<=n;x++)
for(int y=1;y<=n;y++)
for(int z=1;z<=n;z++)
{
if(x==y||z==x||y==z) continue;
int tmp=0;
for(int i=1;i<=n;i++)
if(x!=i&&y!=i&&z!=i&&In(a[x],a[y],a[z],a[i])) tmp++;
f[x][y][z][tmp]=6;
Ct[x][y][z]=tmp;
}
for(int x=1;x<=n;x++)
for(int y=1;y<=n;y++)
for(int z=1;z<=n;z++)
{
if(x==y||z==x||y==z) continue;
if(Ct[x][y][z]==n-3)
{
ans=dfs(x,y,z,0);
}
}
printf("%lld",ans);
return 0;
}

