8.17模拟赛小结

前言

最卡常的一集

T1 激光通讯原题

题意：给你一个大小不超过 $100\times 100$ 的矩阵其中有一个起点，终点和一些障碍物求从起点到终点不碰到障碍物的最小转弯次数

思考一开始肯定是想记忆化 dfs 但是那样写了下发现麻烦于是改成了 bfs
容易发现转弯次数能小就小所以将普通的队列改成一个堆即可
时间复杂度 $O(n^2\log n^2)$

Code

#include<bits/stdc++.h>
#define N 105
using namespace std;
int n,m,sx,sy,ex,ey,ans=1e9;
char c[N][N];
int vis[N][N][2];//0横1竖 
int dx[]={0,0,1,-1},dy[]={1,-1,0,0};
struct point {
	int x,y,w,v;
};
bool operator < (point a,point b)
{
	return a.v>b.v;
}
priority_queue <point> q; 
void bfs()
{
	q.push((point){sx,sy,0,0});
	q.push((point){sx,sy,1,0});
	while(!q.empty())
	{
		point x=q.top();
		q.pop();		
		if(x.x>n||x.y>m||x.x<1||x.y<1||c[x.x][x.y]=='*') continue;
		if(x.x==ex&&x.y==ey)
			ans=min(ans,x.v);
		vis[x.x][x.y][x.w]=1;
		for(int i=0;i<2;i++)
		{
			int xx=x.x+dx[i],yy=x.y+dy[i];
			if(vis[xx][yy][0]) continue;
			q.push((point){xx,yy,0,x.v+x.w});
		}
		for(int i=2;i<4;i++)
		{
			int xx=x.x+dx[i],yy=x.y+dy[i];
			if(vis[xx][yy][1]) continue;
			q.push((point){xx,yy,1,x.v+1-x.w});
		}
	}
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>m>>n;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			cin>>c[i][j];
			if(c[i][j]=='C')
				if(sx==0) sx=i,sy=j;
				else ex=i,ey=j;
		}
	bfs();
	cout<<ans;
	return 0;
}

T2 树

题意：已知一棵二叉树点的编号为 $1\to n$ 且中序遍历也为 $1\to n$ 给出这棵树的层次遍历求这棵树的先序遍历

思考：了解过平衡树 BST 堆之类的就知道原树就是一个 BST 因此满足左儿子小于根右儿子大于根的性质因此每个子树都必定是一个区间然后这个子树的根就是层次遍历最靠前的点 于是用一棵线段树维护即可时间复杂度 $O(n\log n)$

#include<bits/stdc++.h>
#define N 300005
using namespace std;
int n,a[N],id[N];//id:每个数的下标 
int tr[4*N];
void Pushup(int x)
{
	if(id[tr[x*2]]>id[tr[x*2+1]]) tr[x]=tr[x*2+1];
	else tr[x]=tr[x*2];
}
void builds(int l,int r,int x)
{
	if(l==r)
	{
		tr[x]=l;
		return;
	}
	int mid=(l+r)/2;
	builds(l,mid,x*2);
	builds(mid+1,r,x*2+1);
	Pushup(x);
}
int query(int l,int r,int L,int R,int x)
{
	if(l>R||r<L) return -1;
	if(l>=L&&r<=R) return tr[x];
	int mid=(l+r)/2;
	int ls=query(l,mid,L,R,x*2),rs=query(mid+1,r,L,R,x*2+1);
	if(ls==-1) return rs;
	if(rs==-1) return ls;
	if(id[ls]>id[rs]) return rs;
	return ls;
}
void solve(int l,int r)
{
	if(l>r) return;
	int root=query(1,n,l,r,1);
	printf("%d ",root);
	solve(l,root-1);
	solve(root+1,r);
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]),id[a[i]]=i;
	builds(1,n,1);
	solve(1,n);
	return 0;
}

T3 石头剪刀布

$n\le 2000$

很毒瘤
错误的思路：前$i$个数最长上升序列长度为$j$ 钦定每次最后取的数是 $k$ 的方案数
因为这道题要求的是全局所以不能钦定一个点

运用全局 dp

设全局状态 $f_{i,p_0,p_1,p_2}$ 表示到了 $i$ 时结尾是 $0,1,2$ 的最长串长度为 $p_0,p_1,p_2$ 考虑转移
易得初始化状态 $f_{0,0,0,0}=1$ 若当前第 $i$ 位取了 $1$ 根据一个小 dp 可知$f_{i-1,p_0,p_1,p_2}$ 就应该贡献给 $f_{i,p_0,max(p_0+1,p_1),p_2}$ 所以可以根据这个枚举 $i,p_0,p_1,p_2$ 最后统计答案时将 $f_{n,p_0,p_1,p_2}$ 贡献给 $ans_{max(p_0,p_1,p_2)}$即可
时间复杂度 $O(n^4)$ 可以得到 40pts
Code

#include<bits/stdc++.h>
#define N 55
#define ll long long
using namespace std;
ll mod=998244353;
int n,a[N][8];
char c[8];
int f[N][N][N][N],ans[N]; 
void add(int &x,int &y)
{
	x=(1ll*x+1ll*y)%mod;
}
int main()
{
	scanf("%d",&n);	
	for(int i=1;i<=n;i++)
	{
		scanf("%s",c+1);
		for(int j=strlen(c+1);j>=1;j--)
			a[i][c[j]-'0']=1;
	}
	f[0][0][0][0]=1;
	for(int i=1;i<=n;i++)
	{
		for(int p0=0;p0<=i;p0++)
		for(int p1=0;p1<=i;p1++)
		for(int p2=0;p2<=i;p2++)
		{
			if(a[i][0]) add(f[i][max(p0,p2+1)][p1][p2],f[i-1][p0][p1][p2]);
			if(a[i][1]) add(f[i][p0][max(p1,p0+1)][p2],f[i-1][p0][p1][p2]);
			if(a[i][2]) add(f[i][p0][p1][max(p2,p1+1)],f[i-1][p0][p1][p2]);
		}
	}
	for(int p0=0;p0<=n;p0++)
	for(int p1=0;p1<=n;p1++)
	for(int p2=0;p2<=n;p2++)
		add(ans[max(p0,max(p1,p2))],f[n][p0][p1][p2]);
	for(int i=1;i<=n;i++)
		printf("%d ",ans[i]);
	return 0;
}

考虑优化这个 dp
容易发现有很多多余状态
可知 $p_0,p_1,p_2$ 其中一个是从任意其它一个加 $1$ 转移过来的因此它们两两之间的差不可能大于2 为什么？已知
$p_0\ge p_2+1$
$p_1\ge p_0+1$
$p_2\ge p_1+1$
结合三项试若满足其中两项则剩余一项一定不满足因此它们的差是不会超过 $2$ 的

所以可以剪枝优化状态

时间复杂度可以优化成 $O(n^2)$ 结合 map 可以艹出 70pts

但是还是过不了我们需要优化空间
容易发现因为是围绕一个数不动的所以可以使用 偏移量 来减少空间复杂度优化成 $n^2$ 的
这样理论上就能通过此题了
但是坑点还是有的比如偏移量要选对还要判断是否大于 $0$
先放一个假 AC 版本的因为卡常还是 70pts T了

#include<bits/stdc++.h>
#define N 2005
#define ll long long
using namespace std;
ll mod=998244353;
int n,a[N][8];
char c[8];
int f[N][N][5][5],ans[N]; 
void add(int &x,int &y)
{
	x=(1ll*x+1ll*y)%mod;
}
int main()
{
	scanf("%d",&n);	
	for(int i=1;i<=n;i++)
	{
		scanf("%s",c+1);
		for(int j=strlen(c+1);j>=1;j--)
			a[i][c[j]-'0']=1;
	}
	f[0][0][2][2]=1;
	for(int i=1;i<=n;i++)
	{
		for(int p0=0;p0<=i;p0++)
		for(int p1=p0+2;p1>=max(p0-2,0);p1--)
		for(int p2=p0+2;p2>=max(p0-2,0);p2--)
		{
			if(a[i][0]) add(f[i][max(p0,p2+1)][p1-max(p0,p2+1)+2][p2-max(p0,p2+1)+2],f[i-1][p0][p1-p0+2][p2-p0+2]);
			if(a[i][1]) add(f[i][p0][max(p1,p0+1)-p0+2][p2-p0+2],f[i-1][p0][p1-p0+2][p2-p0+2]);
			if(a[i][2]) add(f[i][p0][p1-p0+2][max(p2,p1+1)-p0+2],f[i-1][p0][p1-p0+2][p2-p0+2]);
		}
	}
	for(int p0=0;p0<=n;p0++)
	for(int p1=p0+2;p1>=max(p0-2,0);p1--)
	for(int p2=p0+2;p2>=max(p0-2,0);p2--)
		add(ans[max(p0,max(p1,p2))],f[n][p0][p1-p0+2][p2-p0+2]);
	for(int i=1;i<=n;i++)
		printf("%d ",ans[i]);
	return 0;
}

然后我们选择卡常，具体为：

加上 O2 火车头
手写 %
手写 max
使用滚动数组
加上 reg 和 inline
成功从 4000ms 卡成 500ms

#include<bits/stdc++.h>
#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#define N 2023
#define reg register 
#define ll long long
using namespace std;
int mod=998244353;
int n,a[N][8];
char c[8];
int f[2][N][6][6],ans[N]; 
inline void add(int &x,int &y)
{
	x=x+y>mod ? x+y-mod:x+y;
}
inline int max(int x,int y)
{
	return x>y ? x:y;
}
int main()
{
	scanf("%d",&n);	
	for(reg int i=1;i<=n;i++)
	{
		scanf("%s",c+1);
		for(reg int j=strlen(c+1);j>=1;j--)
			a[i][c[j]-'0']=1;
	}
	f[0][0][2][2]=1;
	for(reg int i=1;i<=n;i++)
	{
		memset(f[i&1],0,sizeof f[i&1]);
		for(reg int p0=0;p0<=i;p0++)
		for(reg int p1=p0+2;p1>=max(p0-2,0);p1--)
		for(reg int p2=p0+2;p2>=max(p0-2,0);p2--)
		{
			if(a[i][0]) add(f[i&1][max(p0,p2+1)][p1-max(p0,p2+1)+2][p2-max(p0,p2+1)+2],f[(i-1)&1][p0][p1-p0+2][p2-p0+2]);
			if(a[i][1]) add(f[i&1][p0][max(p1,p0+1)-p0+2][p2-p0+2],f[(i-1)&1][p0][p1-p0+2][p2-p0+2]);
			if(a[i][2]) add(f[i&1][p0][p1-p0+2][max(p2,p1+1)-p0+2],f[(i-1)&1][p0][p1-p0+2][p2-p0+2]);
		}
	}
	for(reg int p0=0;p0<=n;p0++)
	for(reg int p1=p0+2;p1>=max(p0-2,0);p1--)
	for(reg int p2=p0+2;p2>=max(p0-2,0);p2--)
		add(ans[max(p0,max(p1,p2))],f[n&1][p0][p1-p0+2][p2-p0+2]);
	for(reg int i=1;i<=n;i++)
		printf("%d ",ans[i]);
	return 0;
}

T4 快递员

题意：给出 $n\times m4的矩阵每次给出两种操作

1 更改一个点为障碍物/通行
2 查询两点最短路

$n\leq 5,m\leq 5\times 10^5,q\leq 5\times 10^4$

无语了刚才知道第四题题干错了加上这句：

任意时刻不允许往左走

有这种东西就可以考虑了
把询问拆成一列一列的就行了
先预处理好一列内的 $dis_{i,j}$ 表示从 $i$ 到 $j$ 的距离如果中间有障碍物就把它赋值成 $inf$ 即可
现在考虑怎么考虑合并
如果考虑合并相邻的两列怎么和?

容易得到 $dp$ 式
$disc_{i,j}=\min(disa_{i,k}+disb_{k,j}+1)$

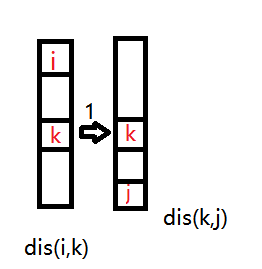
看图一眼理解
然后就会得到一个新的块这个块也可以合并
然后用线段树维护一下即可

注意：因为 $m$ 很大所以不能每次 updata 暴做需要建树

时间复杂度 $O(mn^3+qn^3\log m)$
Code

#include<bits/stdc++.h>
#define M 200005
#define ll long long
using namespace std;
int n,m,q;
struct node{
	int r[6][6];
	int n;
}tr[4*M],t;
int a[6][M];
node clear(int x)
{
	node c;
	c.n=n;
	for(int i=1;i<=c.n;i++)
		for(int j=1;j<=c.n;j++)
			c.r[i][j]=1e9;
	if(x)
	for(int i=1;i<=c.n;i++)
		c.r[i][i]=-1;
	return c;
}
node operator *(node a,node b)
{
	node c=clear(0);
	for(int i=1;i<=c.n;i++)
		for(int j=1;j<=c.n;j++)
			for(int k=1;k<=c.n;k++)
				c.r[i][j]=min(c.r[i][j],a.r[i][k]+b.r[k][j]+1);
	return c;
}
node change(int x)
{
	node c=clear(0);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			int p=0;
			for(int k=min(i,j);k<=max(i,j);k++)
				if(a[k][x]==0) p=1;
			if(p) c.r[i][j]=1e9;
			else c.r[i][j]=abs(i-j);
		}
	}
	return c;
}
void Pushup(int x)
{
	tr[x]=tr[x*2]*tr[x*2+1];
}
void updata(int l,int r,int L,int x)
{
	if(l>L||r<L) return;
	if(l==r)
	{
		tr[x]=change(l);
		return ;
	}
	int mid=(l+r)/2;
	updata(l,mid,L,x*2);
	updata(mid+1,r,L,x*2+1);
	Pushup(x);
}
node query(int l,int r,int L,int R,int x)
{
	if(l>R||r<L) return t;
	if(l>=L&&r<=R) return tr[x];
	int mid=(l+r)/2;
	node ls=query(l,mid,L,R,x*2),rs=query(mid+1,r,L,R,x*2+1);
	if(ls.n==-1) return rs;
	if(rs.n==-1) return ls;
	return ls*rs;
}
void build(int l,int r,int x)
{
	if(l==r)
	{
		tr[x]=change(l);
		return ;
	}
	int mid=(l+r)/2;
	build(l,mid,x*2);
	build(mid+1,r,x*2+1);
	Pushup(x);
}
int main()
{
	t.n=-1;
	scanf("%d%d%d",&n,&m,&q);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			scanf("%d",&a[i][j]);
	build(1,m,1);
	while(q--)
	{
		int opr,sx,sy,ex,ey;
		scanf("%d%d%d",&opr,&sx,&sy);
		if(opr==1)
		{
			a[sx][sy]^=1;
			updata(1,m,sy,1);
		}
		else
		{
			scanf("%d%d",&ex,&ey);
			node c=query(1,m,sy,ey,1);
			printf("%d\n",c.r[sx][ex]==1e9? -1:c.r[sx][ex]);
		}
	}
	return 0;
}

posted @ 2023-08-17 16:32 g1ove 阅读(5) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

g1ove

8.17模拟赛小结

前言

T1 激光通讯 原题

T2 树

T3 石头剪刀布

T4 快递员

公告

T1 激光通讯原题