8.12模拟赛小结
前言
最 ez 的一集
关于 T4
逆天题目
T1 打工 原题
化简题意:有\(n\) 个工作,每个工作有固定的工资截止时间 你可以在 \(1\) 个时间单位内选择一项工作并完成它 求最后最大工资
思考:
诶 好像做个这个题?上次似乎讲过,用反悔贪心来做
思路:
首先讲原工作的截止时间从小到大排序 然后每次遍历一个工作 如果能做就做了 如果做不了就看看之前做过的所有工作中有没有工资比当前工资低的 直接选择不做那个工作 做当前的工作即可
要快速访问一段东西的最小值 用堆优化即可
时间复杂度 \(O(n\log n)\)
Code
#include<bits/stdc++.h>
#pragma GCC optimize(3,"Ofast","inline")
#define mp make_pair
#define ll long long
#define N 2000005
using namespace std;
int n,m;
pair <ll,ll> a[N];
ll ans,last;
priority_queue<ll> q;
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%lld%lld",&a[i].first,&a[i].second),a[i].second*=-1;
sort(a+1,a+1+m);
for(int i=1;i<=m;i++)
{
ll x=-a[i].second;
last+=a[i].first-a[i-1].first;
if(last)
{
ans+=x;
q.push(-x);
last--;
}
else
{
if(q.empty()) continue;
int z=-q.top();
if(x>z) ans-=z,q.pop(),ans+=x,q.push(-x);
}
}
printf("%lld",ans);
return 0;
}
T2 购物 原题
简要题意:有 \(n\) 种货币,每种货币的价值为 \(v_i\) ,你有 \(c_i\) 个,你要支付 \(m\) 元,老板每种货币有无限个,你需要满足你支出的货币数和老板找回你钱的货币数的和最小
思考:
这是一个很容易就想到的完全背包和多重背包的结合体
最难想的问题是上界
比赛时直接猜结论过了(),上界是 \(2m\) ,时间复杂度是\(O(nm\log m)\) 差不多是 \(10^8\) 过了
代码很好写 两个背包就行
难就难在验证结论的正确性
好吧我不会证明(((
看一下第一篇题解的证明吧()
Code
#include<bits/stdc++.h>
#define N 205
#define M 400005
using namespace std;
int n,m,v[N],c[N],q;
int f1[M],f2[M],ans=1e9;
inline void bag(int x,int v)
{
for(int i=q;i>=x*v;i--)
f1[i]=min(f1[i],f1[i-v*x]+x);
}
int main()
{
scanf("%d%d",&n,&m);
q=3*m;
fill(f1,f1+q+2,1e9);
fill(f2,f2+q+2,1e9);
f1[0]=f2[0]=0;
for(int i=1;i<=n;i++)
scanf("%d",&v[i]);
for(int i=1;i<=n;i++)
scanf("%d",&c[i]);
for(int i=1;i<=n;i++)
{
for(int j=v[i];j<=q-m;j++)
f2[j]=min(f2[j],f2[j-v[i]]+1);
int t=1;
while(c[i]>t)
{
bag(t,v[i]);
c[i]-=t;
t*=2;
}
bag(c[i],v[i]);
}
for(int i=m;i<=q;i++)
ans=min(ans,f1[i]+f2[i-m]);
if(ans==1e9) ans=-1;
cout<<ans;
return 0;
}
水了()
T3 魔法 原题
简要题意:给 \(m\) 个字符长度为 \(n\) 可能有 ? 的 \(01\) 串 ?可以当成 0 或 1 来看 给定 \(q\) 次操作 每次会修改一个字符串或者查询区间 \(l\to r\)中有多少个字符串可以解释成该 \(01\) 串
吐槽一下:数据太辣鸡了 能开 \(30\) 棵线段树艹过去 真的无语(((
思考:不妨分类讨论
- 如果 \(l\to r\) 某一位同时存在 \(0\) 和 \(1\) 那么肯定不合法 答案为 \(0\)
- 如果 \(l\to r\) 某一位只有 \(0\),\(1\) 或
?说明这一位固定 对答案没有贡献 - 如果 \(l\to r\) 某一位只有
?说明这一位可以取 \(0\),\(1\) 二者之一 对答案的贡献是 \(\times 2\)
好的我们发现这道题每一位开一棵线段树或者树状数组即可 发现 \(n\leq 30\) 直接暴艹(((
然后交到原题一看 T了(((
分析一下时间复杂度 : \(O(qn\log m) \leq 6\times 10^8\)
能艹过去就是数据水了(((
我们要考虑正解
不妨思考一下,这 \(n\) 棵线段树 每次只存 \(01\) 真的太浪费空间了
我们不妨考虑直接将他们压位压进一个 \(int\) 里
可以用这题了解压位
我们考虑 \(3\) 棵线段树:
- \(0\)树:每个字符串\(1\to 1,0\to 0,?\to 0\)
- \(1\)树:每个字符串\(1\to 0,0\to 1,?\to 0\)
- \(?\)树:每个字符串\(1\to 1,0\to 1,?\to 0\)
每棵线段树存的是他们的或值
为什么?我们把要求的数的那一位都看成 \(0\) 了 显然只有每一位都是 \(0\) 最终的或值才是 \(0\) 然后如果 \(0\) 树和一树查询的值与一下也是 \(0\) 显然方案合法 然后查一下 ? 树区间内有几个 \(0\) 即可
每次操作一次是 \(\log m\) 的 查询一次位数是 \(O(n)\) 的
时间复杂度 \(O(q(n+\log m))\)
Code
#include<bits/stdc++.h>
#define M 100055
using namespace std;
struct segtree{
int tr[4*M];
inline void Pushup(int x)
{
tr[x]=tr[x*2]|tr[x*2+1];
}
inline void updata(int l,int r,int L,int x,int v)
{
if(l>L||r<L) return;
if(l==r)
{
tr[x]=v;
return;
}
int mid=(l+r)/2;
updata(l,mid,L,x*2,v);
updata(mid+1,r,L,x*2+1,v);
Pushup(x);
}
inline int query(int l,int r,int L,int R,int x)
{
if(l>R||r<L) return 0;
if(l>=L&&r<=R) return tr[x];
int mid=(l+r)/2;
return query(l,mid,L,R,x*2)|query(mid+1,r,L,R,x*2+1);
}
}tr[3];
int n,m,q,ans;
string s;
inline void modify(int x,string s)
{
int s1=0,s2=0,s3=0,t=1;
for(int i=0;i<n;i++)
{
if(s[i]=='0') s2|=t,s3|=t;
if(s[i]=='1') s1|=t,s3|=t;
t*=2;
}
tr[0].updata(1,m,x,1,s1);
tr[1].updata(1,m,x,1,s2);
tr[2].updata(1,m,x,1,s3);
}
inline int ask(int l,int r)
{
int s1=tr[0].query(1,m,l,r,1);
int s2=tr[1].query(1,m,l,r,1);
int s3=tr[2].query(1,m,l,r,1);
if((s1&s2)==0)
{
int sum=0;
while(s3)
{
sum++;
s3-=s3&-s3;
}
return 1<<(n-sum);
}
else return 0;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m>>q;
for(int i=1;i<=m;i++)
{
cin>>s;
modify(i,s);
}
while(q--)
{
int opr,l,r,x;
cin>>opr;
if(opr==0)
{
cin>>l>>r;
ans^=ask(l,r);
}
else
{
cin>>x>>s;
modify(x,s);
}
}
cout<<ans;
return 0;
}
T4 和平
来补 T4 了((
放一下原题 
化简题意:有一棵 \(n\) 个点 的树 你要在里面选 \(m\) 条长度不超过 \(k\) 的边 保证不能存在一个点被所有边覆盖
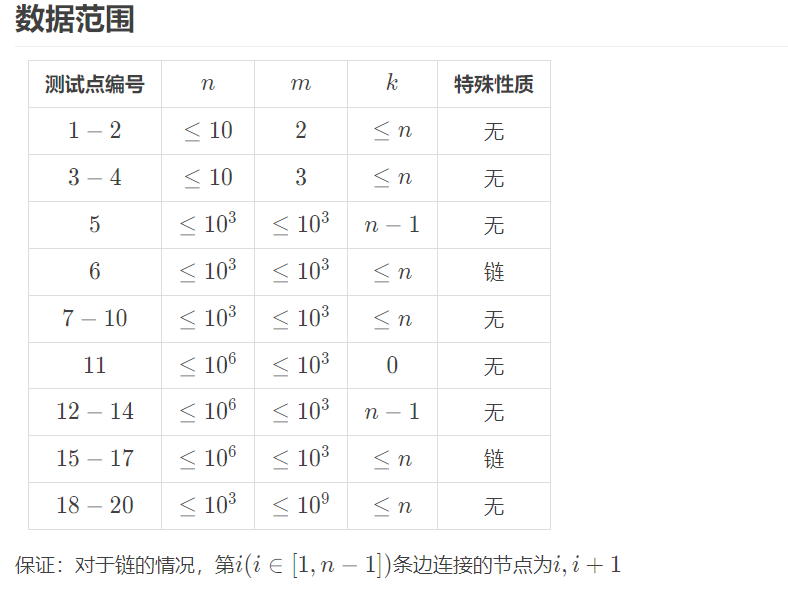
看一眼数据范围就会发现这道题也太毒瘤了
出题人脑子开了个光 为了强迫你打部分分开了个若至测试点 \(11\to 17\) 背后的原因令人寒心
为什么这题考场上没人写出来?困难的思路再加上四个部分的分类讨论,太毒瘤了
现在开始正题
思路:
这种题保证一个点不能被覆盖太难了 遇难则反 考虑容斥 (难度:1)
考虑一个子集 \(S \in n\) 其中 \(S\) 内的点必须被 \(m\)条边包含 并求出情况数 \(x\) 那么对答案的贡献为 \(-1^{|S|}\times x\) 这是一个经典容斥 暴搜能过 \(4\) 个点
好了正常人的思路到这里已经止步于此了 然后就是正解的思路:
考虑这个集合 这个集合十分特殊 它里面的点必须满足的条件是 在一条路径上
为什么?因为他必须被 \(m\) 条边包含 这是最关键的
歪一条都不行
考虑枚举每个集合 \((|S|>2)\) 路线上最左边合最右边的点 所有的边都必须经过这两个点 因此都必须经过这条路径上的所有点 所以我们可以得到一个重要到正常人想不出来的结论:
什么意思呢?就是已经确定了起点重点 然后中间的点随便取贡献一样
然后就到了最天才的部分
可以得到贡献为:
我们知道二项式定理:
证明的话将 \((1+x)^n\) 中 \(x=1\) 和 \(x=-1\)的情况带入 暴力拆解即可
所以上面的式子贡献为\(0\)
因此,只需考虑 \(|S|=0\) 和 \(|S|=1\) 的情况
所以,贡献为:所有长度不超过 \(k\) 的边 \(-\) \(m\)条边包含一个点的情况 + \(m\)条边包含一条边的情况
于是有人就给他取了个名字:点减边容斥
上面的点 \(O(n^2)\) 暴做就行了
做法可以参考树上背包合并或者点分治即可
可以先求出一条边合理情况 \(m\) 条边就是一个乘法原理
一般来说这道题结束了 但是 若至出题人给出了若至数据 让你必须思考部分分 吐了
- \(1.k=0\) 很简单 只能走\(0\) 条边 所有情况就是\(n^m\) 不合法情况就是 \(n\) 很简单
- \(2.k=n-1\) 还行的难度 能随便走 所有的情况很明显为 \(C(n,2)+n\) 不合法的情况
dfs搞一下合并即可 - \(3.\text{一条链}\) 这是最若至最牛魔的点 好好的问题还要考虑树上情况再做一次 属实若至 接下来分析做法 可以将 \(k\) 距离改成移动窗口搞 然后有一些
for就可以用等差数列公式搞就行
三个部分分 时间复杂度 \(O(n)\)
这道题终于完结撒花了
Code
#include<bits/stdc++.h>
#define N 1005
#define ll long long
using namespace std;
ll mod=998244353;
int n,m,k;
int root;
int head[N*N],tot=1;
struct edge{
int fr,to,next;
}e[N*N*2];
void add(int u,int v)
{
e[tot]=(edge){u,v,head[u]};
head[u]=tot++;
}
ll all,sum[N],t[N];
int dis[N];
int q[N],l,r;
void Getdis(int now,int fa,int dep)
{
if(dep>k) return;
if(now>=root) q[++r]=dep;
for(int i=head[now];i;i=e[i].next)
{
int son=e[i].to;
if(son==fa) continue;
Getdis(son,now,dep+1);
}
}
ll solve(int now,int fa)
{
ll cnt=1;
fill(dis,dis+1+n,0);
l=1,r=0;
dis[0]=1;
for(int i=head[now];i;i=e[i].next)
{
int son=e[i].to;
if(son==fa) continue;
Getdis(son,now,1);
sum[0]=1;
for(int j=1;j<=k;j++)
sum[j]=(sum[j-1]+dis[j])%mod;
for(int j=l;j<=r;j++)
cnt=(cnt+sum[k-q[j]])%mod;
for(;l<=r;l++)
dis[q[l]]++;
}
return cnt;
}
void dfs(int now,int fa)
{
root=now;
all=(all+solve(now,fa));
for(int i=head[now];i;i=e[i].next)
{
int son=e[i].to;
if(son==fa) continue;
dfs(son,now);
}
}
ll Qpow(ll a,int x)
{
ll sum=1;
while(x)
{
if(x&1) sum=sum*a%mod;
a=a*a%mod;
x/=2;
}
return sum;
}
void query1e3()
{
for(int i=1;i<=n-1;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
add(v,u);
}
//求All
dfs(1,0);
all=Qpow(all,m);
//求点
for(int i=1;i<=n;i++)
{
root=0;
all=(all-Qpow(solve(i,0),m)+mod)%mod;
}
//求边
k--;
for(int i=1;i<tot;i+=2)
{
root=0;
int u=e[i].fr,v=e[i].to;
solve(u,v);
t[0]=1;
for(int j=1;j<=k;j++)
t[j]=dis[j];
solve(v,u);
sum[0]=1;
for(int j=1;j<=k;j++)
sum[j]=(sum[j-1]+dis[j])%mod;
ll tmp=0;
for(int j=0;j<=k;j++)
tmp=(tmp+t[j]*sum[k-j]%mod)%mod;
all=(all+Qpow(tmp,m))%mod;
}
cout<<all;
}
int size[N*N];
void dfsk(int now,int fa)
{
size[now]=1;
ll tmp=1;
for(int i=head[now];i;i=e[i].next)
{
int son=e[i].to;
if(son==fa) continue;
dfsk(son,now);
tmp=(tmp+1ll*size[now]*size[son])%mod;
size[now]+=size[son];
}
tmp=(tmp+1ll*size[now]*(n-size[now]))%mod;
all=(all-Qpow(tmp,m)+Qpow(1ll*size[now]*(n-size[now])%mod,m)+mod)%mod;
}
void queryk()
{
all=Qpow(1ll*n*(n-1)/2%mod+n,m);
for(int i=1;i<=n-1;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
add(v,u);
}
dfsk(1,0);
cout<<all;
return;
}
void query3()
{
for(int i=1;i<=k+1;i++)
all=(all+n-i+1)%mod;
all=Qpow(all,m);
for(int i=1;i<=n;i++)
{
int l=min(i-1,k),r=min(n-i,k);
ll tmp=l+1;
tmp+=1ll*(k-l+r)*(r-k+l+1)/2%mod;
tmp+=1ll*(k-r)*r%mod;
all=(all-Qpow(tmp,m)+mod)%mod;
}
k--;
for(int i=1;i<=n-1;i++)
{
int l=min(i-1,k),r=min(n-i-1,k);
ll tmp=l+1;
tmp+=1ll*(k-l+r)*(r-k+l+1)/2%mod;
tmp+=1ll*(k-r)*r%mod;
all=(all+Qpow(tmp,m))%mod;
}
cout<<all;
return;
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
if(n<=1000)
{
query1e3();
return 0;
}
if(k==0) printf("%lld\n",(Qpow(n,m)-n+mod)%mod);
else if(k==n-1) queryk();
else query3();
return 0;
}
第四题写自闭了 起码 \(3\) 个小时起步

