学习笔记:AC自动机
0.前言
emmmm我也是一知半解,写篇笔记梳理思路 毒瘤夏令营真不把人看啊一天两三个难度算法
1.产生原因
kmp,一个串匹配另一个串的线性高效写法
但是如果是多个匹配串呢?
跑kmp可以达到\(O(nm)\)的复杂度
太美丽啦kmp!还是看一下远处的AC自动机吧家人们
但是如果是AC自动机就可以做到\(O(|S|)\)的复杂度
2.流程
1.失配数组
我们发现匹配时如果失败就重跑实在是太费时间了!
我们可以借鉴kmp的思想,搞一个失配数组
先把所有的匹配串扔进一颗字典树里面
匹配失败只要跳到和当前字符串有相同最长后缀尽节点上是最优的
和kmp不一样,kmp求的是相同前后缀
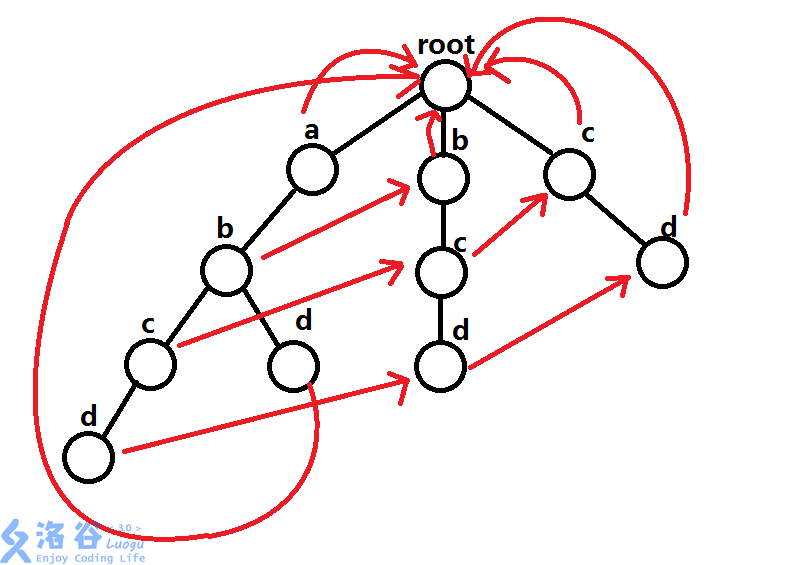
(网图 侵删)
看,左边是abcd失配后应该跳到相同后缀bcd上
bcd失配后又到cd上 十分合理
而虽然abd那里也有d,可是它们得有相同的后缀啊!

可以发现,两个s指向的都是7节点。
-
找到6的父节点5,5的fail指针指向10,然而10结点没有字母's'连出的边;
-
所以跳到10的fail指针指向的结点0,发现0结点有字母's'连出的边,指向7结点;
-
所以fail6=7.
接下是创建过程(Copy)
构造失配(fail)指针
在讲构造以前,先来对比一下这里的fail指针与KMP中的next指针:
共同点-两者同样是在失配的时候用于跳转的指针。
不同点-KMP要求的是最长相同真前后缀,而AC自动机只需要相同后缀即可。
因为KMP只对一个模式串做匹配,而AC自动机要对多个模式串做匹配。
有可能fail指针指向的结点对应着另一个模式串,两者前缀不同。
也就是说,AC自动机在对匹配串做逐位匹配时,同一位上可能匹配多个模式串。
因此fail指针会在字典树上的结点来回穿梭,而不像KMP在线性结构上跳转。
下面介绍构建fail指针的基础思想:(强调!基础思想!基础!)
构建fail指针,可以参考KMP中构造next数组的思想。
我们利用部分已经求出fail指针的结点推导出当前结点的fail指针。具体我们用BFS实现:
如果结点fail[p]通过字母c连接到的子结点w存在:
如果fail[p]通过字母c连接到的子结点w不存在:
则让u的fail指针指向这个结点w(fail[u]=w)。
相当于在p和fail[p]后面加一个字符c,就构成了fail[u]。
那么我们继续找到fail[fail[p]]指针指向的结点,重复上述判断过程,一直跳fail指针直到根节点。
如果真的没有,就令fail[u]=根节点。
考虑字典树中当前的节点u,u的父节点是p,p通过字符c的边指向u。
假设深度小于u的所有节点的fail指针都已求得。那么p的fail指针显然也已求得。
我们跳转到p的fail指针指向的结点fail[p];
如此即完成了fail指针的构建
说人话就是:
- 1.若当前有节点,他的后继就是祖先的失配节点的同一后继(也许没有后继,后面讲)
- 2.若祖先没有节点,只能再往上跳失配值找到有的节点
可以发现是能用递推推的 只需要现在的儿子指向祖先的失配节点的同一后继 - 3.因为可能跳去失配节点会去别的树枝,但深度不会低,所以应该选择bfs而不是dfs
Code:
void get_fail()
{
l=1;//queue:l~r
for(int i=1;i<=26;i++)
if(tr[0][i])//预处理
{
int to=tr[0][i];
fail[to]=0;
q[++r]=to;
}
while(l<=r)
{
int x=q[l++];
for(int i=1;i<=26;i++)
{
int to=tr[x][i];
if(to)//步骤1
{
fail[to]=tr[fail[x]][i];
q[++r]=to;
}
else//步骤2
tr[x][i]=tr[fail[x]][i];
}
}
}
2.求答案
你已经搞了字典树,可以直接开始便历了
- 从根节点开始
- 有子节点 ->直接跳过去
- 没有子节点 fail数组预处理时已经处理好了失配跳的值,实际上直接跳就行了
考虑到了 \(x\) 点
- 1.直接按照fail数组网上跳就好啦 因为如果一个字符串匹配成功了,那么它的后缀一定也是成功匹配的,所以它的失配点也是可以匹配的
-
2.如果不匹配,那么可以往失配数组前移,为啥叫失配数组嘛,失配了就缩小范围。
-
3.因为一直跳到尾,重复只算一次,所以要打标记看来过没有
-
4.原理其实就是在从1~len遍历每个字符,然后在查询的过程其实就是在当前i时,求出来的最长符合的后缀。没有符合的?往上跳!
…<---------->
…………<---->
…………… <->
差不多就是减少长度 像kmp一样
Code:
int query(string s)
{
int now=0,sum=0;
for(int i=0;i<s.size();i++)
{
now=tr[now][s[i]-'a'+1];
int t=now;
while(t&&end[t]!=-1)
{
sum+=end[t];
end[t]=-1;
t=fail[t];
}
}
return sum;
}
完整code:
#include<bits/stdc++.h>
#define ll long long
#define MAXN 1000005
using namespace std;
int n;
string s;
int cnt;
int q[MAXN],l,r;
int tr[MAXN][28],end[MAXN],fail[MAXN];
void insert(string s)
{
int now=0;
for(int i=0;i<s.size();i++)
{
int c=s[i]-'a'+1;
if(!tr[now][c]) tr[now][c]=++cnt;
now=tr[now][c];
}
end[now]++;
}
void get_fail()
{
l=1;//queue:l~r
for(int i=1;i<=26;i++)
if(tr[0][i])
{
int to=tr[0][i];
fail[to]=0;
q[++r]=to;
}
while(l<=r)
{
int x=q[l++];
for(int i=1;i<=26;i++)
{
int to=tr[x][i];
if(to)
{
fail[to]=tr[fail[x]][i];
q[++r]=to;
}
else
tr[x][i]=tr[fail[x]][i];
}
}
}
int query(string s)
{
int now=0,sum=0;
for(int i=0;i<s.size();i++)
{
now=tr[now][s[i]-'a'+1];
int t=now;
while(t&&end[t]!=-1)
{
sum+=end[t];
end[t]=-1;
t=fail[t];
}
}
return sum;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)
cin>>s,insert(s);
cin>>s;
get_fail();
cout<<query(s);
return 0;
}
对应板子:AC自动机模板
初级版学习完毕 头好痒,要长脑子了
AC自动机加强版
好了你已经学会初级版了,接下来是进阶版
传送门:加强版
其实这个也是十分简单啦,只要你了解了模板暴力跳就彳亍了,这题的\(N\)也十分的小,才70,每次跳也70,我们可以暴力得到\(O(GN|T|)\)的复杂度,加几个读入优化就跑过去了
Code:
#include<bits/stdc++.h>
#define MAXN 155
#define MAXM 155*70
using namespace std;
int n,sum[MAXN];
int q[MAXM],l,r;
string s[MAXN],str;
int cnt,tr[MAXM][28],fail[MAXM],id[MAXM];
void init()
{
cnt=l=r=0;
fill(&tr[0][0],&tr[MAXM-5][0],0);
fill(fail,fail+MAXM-5,0);
fill(id,id+MAXM-5,0);
fill(sum,sum+MAXN-2,0);
}
void insert(string s,int num)
{
int now=0;
for(int i=0;i<s.size();i++)
{
int c=s[i]-'a'+1;
if(!tr[now][c]) tr[now][c]=++cnt;
now=tr[now][c];
}
id[now]=num;
}
void get_fail()
{
for(int i=1;i<=26;i++)
if(tr[0][i]) q[++r]=tr[0][i];
while(l<r)
{
int now=q[++l];
for(int i=1;i<=26;i++)
if(tr[now][i])
{
fail[tr[now][i]]=tr[fail[now]][i];
q[++r]=tr[now][i];
}
else tr[now][i]=tr[fail[now]][i];
}
}
void AC_query(string s)
{
int now=0;
for(int i=0;i<s.size();i++)
{
now=tr[now][s[i]-'a'+1];
int t=now;
while(t)
{
sum[id[t]]++;
t=fail[t];
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
while(cin>>n)
{
if(n==0) break;
init();
for(int i=1;i<=n;i++)
cin>>s[i],insert(s[i],i);
get_fail();
cin>>str;
AC_query(str);
int maxx=-1;
for(int i=1;i<=n;i++)
if(sum[i]>maxx) maxx=sum[i];
cout<<maxx<<"\n";
for(int i=1;i<=n;i++)
if(sum[i]==maxx) cout<<s[i]<<"\n";
}
return 0;
}
加强版就完啦 加强了个寂寞
真正的加强版:AC自动机加强加强版
传送门:加强加强版
这就是真正的难题了奥
要是像加强版一样做\(O(|S||T|)\) \(1e11\)的复杂度直接T飞
那咋办?
我们仔细联想一下,就像我们做初级版时,经过一个点给它打个标记 那我们是不是也能这样呢?把经过的点打好标记,最后扫一遍不就好了嘛
我们知道fail数组指向的点的深度一定是比自己小的,然后往自己小的点上跳
诶,指向深度小,不会指回来,\(n\)个点 \(n-1\) 条边,联通性,这不就是树嘛
跑一边dfs之后,求自己的子树和不就是答案了嘛
时间复杂度很好的被优化到了\(O(|T|+|S|)\)
Code:
#include<bits/stdc++.h>
#define MAXN 200005
using namespace std;
int n,cnt,sum[MAXN];
int q[MAXN],l,r;
string s[MAXN],op;
int tr[MAXN][28],fail[MAXN],id[MAXN];
int head[MAXN],tot=1;
struct edge{
int to,next;
}e[MAXN];
void add(int u,int v)
{
e[tot].to=v;
e[tot].next=head[u];
head[u]=tot++;
}
void insert(string s,int num)
{
int now=0;
for(int i=0;i<s.size();i++)
{
int c=s[i]-'a'+1;
if(!tr[now][c]) tr[now][c]=++cnt;
now=tr[now][c];
}
id[num]=now;
}
void getfail()
{
for(int i=1;i<=26;i++)
if(tr[0][i]) q[++r]=tr[0][i];
while(l<r)
{
int now=q[++l];
for(int i=1;i<=26;i++)
if(tr[now][i])
{
fail[tr[now][i]]=tr[fail[now]][i];
q[++r]=tr[now][i];
}
else tr[now][i]=tr[fail[now]][i];
}
}
void AC_query(string s)
{
int now=0;
for(int i=0;i<s.size();i++)
{
now=tr[now][s[i]-'a'+1];
sum[now]++;
}
}
void dfs(int now)
{
for(int i=head[now];i;i=e[i].next)
{
int son=e[i].to;
dfs(son);
sum[now]+=sum[son];
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)
cin>>s[i],insert(s[i],i);
getfail();
for(int i=1;i<=cnt;i++)
add(fail[i],i);
cin>>op;
AC_query(op);
dfs(0);
for(int i=1;i<=n;i++)
cout<<sum[id[i]]<<"\n";
return 0;
}
好了你已经走出AC自动机的新手村了,接下来就是各种毒瘤变种题目了!
练习题:click here (题解)
DP题:here



