数据结构与算法之图
1.图的使用场景一般是关系型的数据载体搭建,图的表示通常可以是邻接矩阵或邻接链表,各自都有优缺点,邻接矩阵快,邻接链表占内存小
2.图的搜索,分为深度优先(DFS)和广度优先(BFS):
深度优先:从某个节点开始一路往下走到不能再走或找到目标值为止
广度优先:从某个节点开始,一次只移动一层,但这一层要将与该节点关联的所有情况都包含进去,然后进入下一层依次往下继续重复上述步骤
3.下面是代码:
3.1 BFS.java
package com.hfm.util;
import java.util.Objects;
class Point{
int x;
int y;
int data;
public Point(int x, int y,int data) {
this.x = x;
this.y = y;
this.data = data;
}
@Override
public String toString() {
return "Point{" +
"x=" + x +
", y=" + y +
", data=" + data +
'}';
}
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
Point point = (Point) o;
return x == point.x && y == point.y && data == point.data;
}
@Override
public int hashCode() {
return Objects.hash(x, y, data);
}
}
public class BFS {
Point dest; //目标位置
Point start; //开始位置
Point map[][]; //地图点
int hlen;
int vlen;
Point direct[] = {
new Point(0,-1,0),
new Point(1,0,0),
new Point(0,1,0),
new Point(-1,0,0),
};
public BFS(Point dest, Point start, Point[][] map,int hlen,int vlen) {
this.dest = dest;
this.start = start;
this.map = map;
this.hlen = hlen;
this.vlen = vlen;
}
public void search(){
boolean mark[][] = new boolean[hlen][vlen];
mark[start.x][start.y] = true;
Point cur = start;
int max = 0;
boolean finished = false;
while (max<hlen*vlen&&!finished){
for (int i = 0; i < direct.length; i++) {
int hindex = cur.x+direct[i].x;
int vindex = cur.y+direct[i].y;
if(hindex<0||hindex>hlen-1||vindex<0||vindex>vlen-1)
continue;
if(!mark[hindex][vindex]){
Point newPoint = new Point(hindex,vindex,map[hindex][vindex].data);
mark[hindex][vindex] = true;
if(newPoint.equals(dest)){
System.out.println("找到了,在["+hindex+","+vindex+"]");
finished = true;
break;
}
max++;
}
}
cur = map[max/vlen][max%vlen];
}
if(max >= hlen*vlen)
System.out.println("没有找到");
}
public static void main(String[] args) {
int mapData[][] = {
{0,0,1,0},
{0,0,0,0},
{0,0,1,0},
{0,1,0,0},
{0,0,0,1},
};
int row = 5;
int col = 4;
Point map[][] = new Point[row][col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
map[i][j] = new Point(i,j,mapData[i][j]);
}
}
BFS bfs = new BFS(map[2][3],map[0][0],map,row,col);
bfs.search();
}
}
3.2.DFS.java
package com.hfm.util;
public class DFS {
Point dest; //目标位置
Point start; //开始位置
Point map[][]; //地图点
int hlen;
int vlen;
boolean mark[][];
int minStep = Integer.MAX_VALUE;
String trace ;
Point direct[] = {
new Point(0,-1,0),
new Point(1,0,0),
new Point(0,1,0),
new Point(-1,0,0),
};
public DFS(Point dest, Point start, Point[][] map,int hlen,int vlen) {
this.dest = dest;
this.start = start;
this.map = map;
this.hlen = hlen;
this.vlen = vlen;
this.mark = new boolean[hlen][vlen];
mark[start.x][start.y] = true;
}
public void search(Point cur,int step,String trace){
if(cur.equals(dest)){
this.minStep = step<this.minStep?step:this.minStep;
this.trace = trace;
return;
}
for (int i = 0; i < direct.length; i++) {
int hindex = cur.x+direct[i].x;
int vindex = cur.y+direct[i].y;
if(hindex<0||hindex>hlen-1||vindex<0||vindex>vlen-1)
continue;
if(!mark[hindex][vindex]&&map[hindex][vindex].data==0){
mark[hindex][vindex] = true;
search(map[hindex][vindex],step+1,trace+"->["+map[hindex][vindex].x+","+map[hindex][vindex].y+"]");
mark[hindex][vindex] = false;
}
}
}
public static void main(String[] args) {
int mapData[][] = {
{0,0,1,0},
{0,0,0,0},
{0,0,1,0},
{0,1,0,0},
{0,0,0,1},
};
int row = 5;
int col = 4;
Point map[][] = new Point[row][col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
map[i][j] = new Point(i,j,mapData[i][j]);
}
}
DFS dfs = new DFS(map[2][3],map[0][0],map,row,col);
dfs.search(map[0][0],0,"["+map[0][0].x+","+map[0][0].y+"]");
System.out.println(dfs.minStep);
System.out.println(dfs.trace);
}
}
上述解决的问题,广度优先算法是逐个找,找到时输出目标所在的节点位置,值为1表示该节点不能通过,0表示可以通过
深度优先是一直找,找到是输出最短路径和走过的路径下标,值为1表示该节点不能通过,0表示可以通过
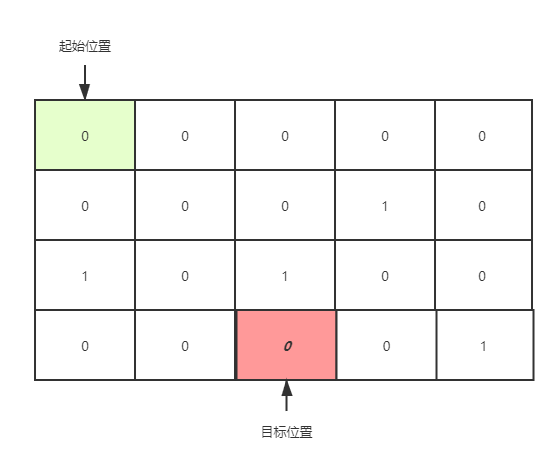
DFS运行结果: