第三次软件工程作业——最大连续子数组和（最大子段和）

一、Github网址：

https://github.com/Rafael-Gu/The-3rd-Homework/tree/master/Q1

老师！！！老师！！！这是我问题一的作业！！！第二问我也做了，也是同一个网址。。。第一题是Q1的文件夹里面！！！

---

二、问题描述

题目(1)：最大连续子数组和（最大子段和）
问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
-- 引用自《百度百科》

---

三、流程图

流程图如下：

---

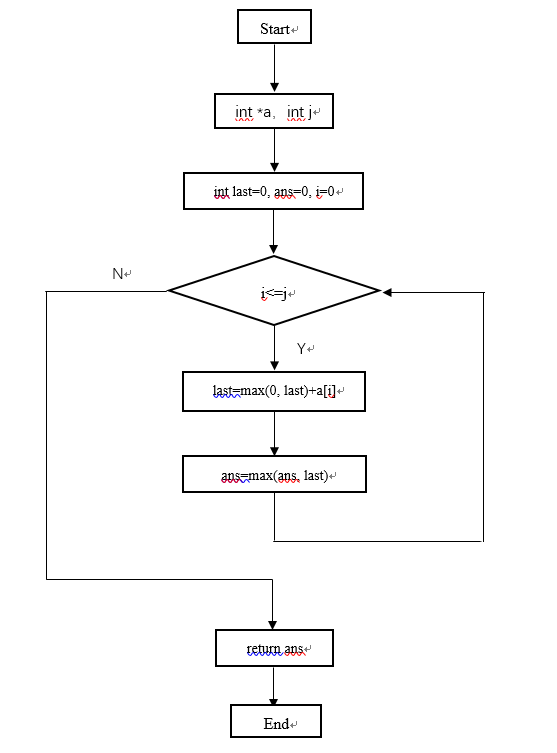
四、程序源代码

程序源代码如下：

#include <stdio.h>
#include <algorithm>
using namespace std;

int sum(int *a,int j)
{
	int last = 0, ans = 0, i = 0;
	for (i = 1; i <= j; i++)
	{
		last = max(0, last) + a[i];
		ans = max(ans, last);
	}
	return ans;
}

int main()
{
	return 0;
}

---

五、条件组合覆盖测试

首先，程序中含有一个for循环，其中for的条件中有一个条件需要满足i=j此条件，其中for调用了一次max函数，而max函数的具体逻辑如下：

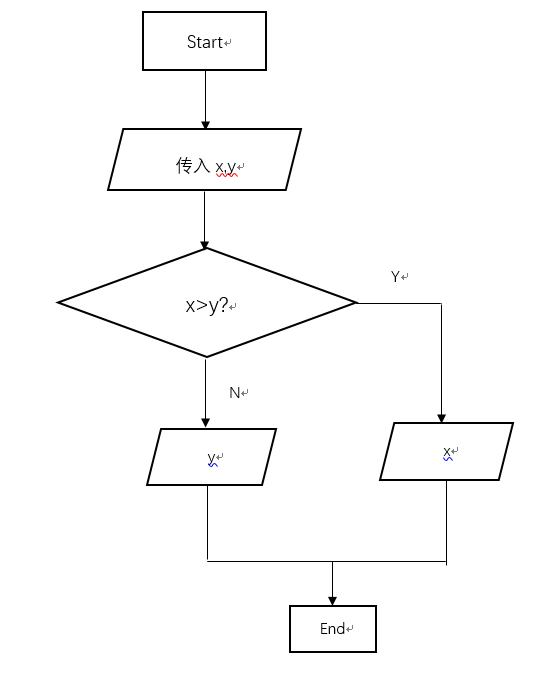
由这两个流程图可知，此处有两个条件需要进行考虑，一个是for中的i<=j；另一个是max函数中的判定条件。

---

六、单元测试代码：

namespace 作业三
{		
	TEST_CLASS(UnitTest1)
	{
	public:
		
		TEST_METHOD(TestMethod1)
		{
			int a[] = { -1,-6,-3,-5,-1 };
			Assert::AreEqual(sum(a, 5), 0);
		}
		TEST_METHOD(TestMethod2)
		{
			int *a = 0;
			Assert::AreEqual(sum(a, 0), 0);
		}
		TEST_METHOD(TestMethod3)
		{
			int a[] = { -1,-6,-5,-3,-5,-2,6 };
			Assert::AreEqual(sum(a, 7), 6);
		}
		TEST_METHOD(TestMethod4)
		{
			int a[] = { 0,-2,2,5,-9,0,7,5,13,-4,-6 };
			Assert::AreEqual(sum(a, 11), 25);
		}
		TEST_METHOD(TestMethod5)
		{
			int a[] = { 1,-2,3,-4,5,-6,7,-8 };
			Assert::AreEqual(sum(a, 8), 7);
		}
	};
}

此组数据，我采用了全为负数、正负数交替输入的几种类型，对程序进行单元测试，单元测试结果全部正确。

---

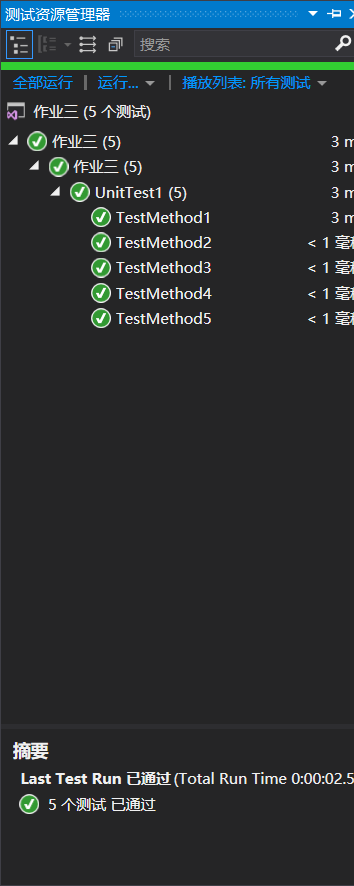
老师！老师！这是我另外做的问题一！问题二我也做了！问题一真的比问题二难啊！

这次作业学会了如何进行条件组合判定，以及强化了单元测试的操作