DS博客作业04--图
0.PTA得分截图

1.图知识总结
1.1 图的相关名词解释
-
(V1,V2) 和 <V1,V2> 的区别:无向图中描述两顶点(V1 和 V2)之间的关系用 (V1,V2) 来表示,而有向图中描述从 V1 到 V2 的"单向"关系用 <V1,V2> 来表示。
-
路径:从一个顶点到另一顶点途径的所有顶点组成的序列(包含这两个顶点),称为一条路径。
-
回路:如果路径中第一个顶点和最后一个顶点相同,即形成一个环,则此路径称为"回路"(或"环")。
-
权和网:在某些实际场景中,图中的每条边会被赋予一个实数来表示一定的含义,这些实数被称为“权”,而带权的图被称为“网”。
-
稀疏图和稠密图:如果图中具有很少的边,此图就称为"稀疏图";反之,则称此图为"稠密图"。判断条件是:e<nlogn,其中 e 表示图中边(或弧)的数量,n 表示图中顶点的数量。如
果式子成立,则为稀疏图;反之为稠密图。
-
完全图:图中各个顶点都与除自身外的其他顶点有边相连具有 n 个顶点的完全图,图中边的数量为 n(n-1)/2;而对于具有 n 个顶点的有向完全图,图中弧的数量为 n(n-1)。
-
连通图与连通分量:无向图中,如果任意两个顶点之间都能够连通,则称此无向图为连通图。若无向图不是连通图,但图中存储某个子图符合连通图的性质,则称该子图为连通分量,如下
图:
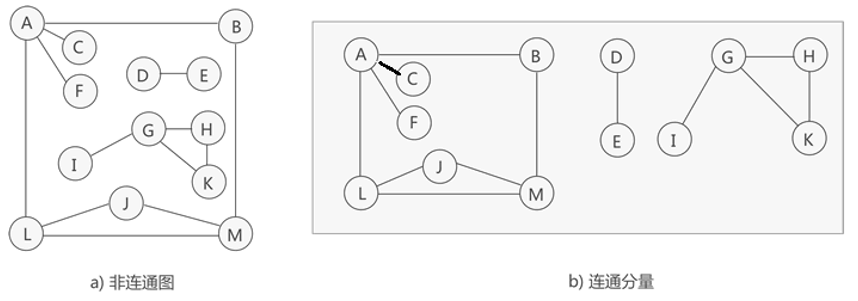
-
强连通图与强连通分量:有向图中,若任意两个顶点 Vi 和 Vj,满足从 Vi 到 Vj 以及从 Vj 到 Vi 都连通,也就是都含有至少一条通路,则称此有向图为强连通图。若有向图本身不是
强连通图,但其包含的最大连通子图具有强连通图的性质,则称该子图为强连通分量,如下图:
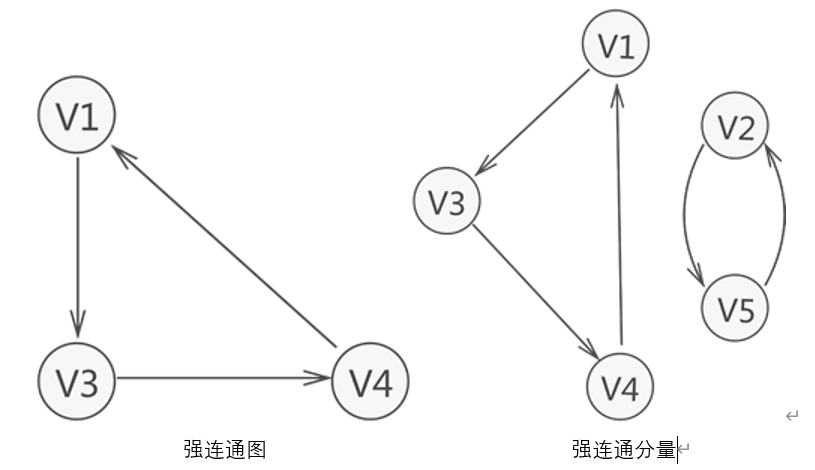
1.2 图存储结构
1.2.1 邻接矩阵
-
介绍:使用二维数组存储图中顶点之间的关系,如果顶点之间存在边,在相应位置用 1 表示,反之用 0 表示;如果碰到带权图(即网),顶点之间有边时在数组的相应位置存储其权值,反
之用 0 表示,如下图:
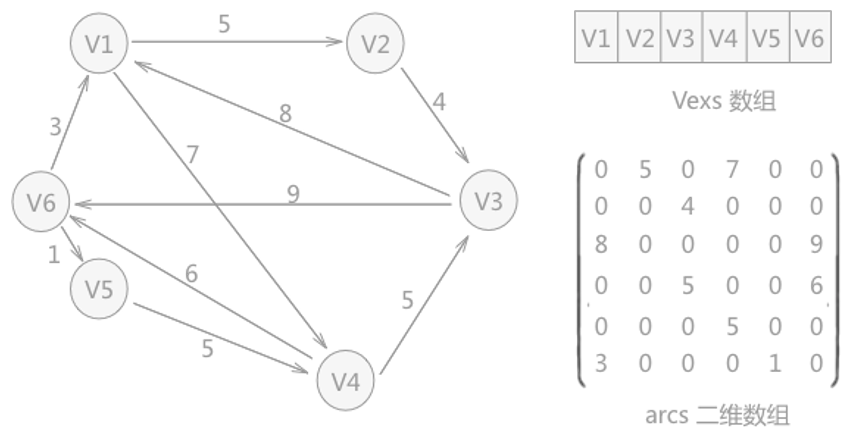
-
邻接矩阵特性:
1.无向图的邻接矩阵一定是对称的,而有向图的邻接矩阵不一定对称。
2.无向图邻接矩阵的第i行(或第i列)非零元素的个数正好是第i个顶点的度。
3.有向图邻接矩阵中,遍历行并统计该行非零元素个数可得该行所对应顶点的出度,遍历列并统计该列非零元素个数可得该列所对应顶点的入读。
4.对无向图的邻接矩阵而言,可以只存矩阵上三角或下三角部分。
5.邻接矩阵适合存储稠密图。
-
结构体定义:
typedef struct //图的定义
{
int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,弧数
} MGraph; //图的邻接矩阵表示类型
- 代码实现:
void CreateMGraph(MGraph& g, int n, int e)//建无向图
{
int i, j, a, b;
g.e = e;
g.n = n;
for (i = 1; i < g.n; i++)
for (j = 1; j < g.n; j++)
g.edges[i][j] = 0; //初始化邻接矩阵
for (i = 1; i <= g.e; i++)
{
cin >> a >> b;
g.edges[a][b] = 1;
g.edges[b][a] = 1;
}
}
1.2.2 邻接表
-
介绍:给图中的各个顶点独自建立一个链表并将所有链表的头节点存储到一个数组中,链表中其他节点存储各自相邻顶点,如下图:

-
邻接表特性:
1.n个顶点e条边的有向图,它的邻接表中有n个顶点表结点和e个边表结点。
2.n个顶点e条边的无向图,它的邻接表中有n个顶点表结点和2e个边表结点。
-
结构体定义:
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct
{ AdjList adjlist; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
- 代码实现:
void CreateAdj(AdjGraph*& G, int n, int e)
{
int i;
G = new AdjGraph;
G->e = e;
G->n = n;
for (i = 1;i <= n;i++) {
G->adjlist[i].firstarc = NULL;
}
for (i = 1;i <= e;i++)
{
int a, b;
cin >> a >> b;
ArcNode* p, * q;
p = new ArcNode;
q = new ArcNode;
p->adjvex = b;
q->adjvex = a;
p->nextarc = G->adjlist[a].firstarc;
G->adjlist[a].firstarc= p;
q->nextarc = G->adjlist[b].firstarc;
G->adjlist[b].firstarc= q;
}
}
1.3 图的遍历
1.3.1 深度遍历(DFS)
- 用邻接矩阵表示
void DFS(MGraph g, int v)//深度遍历
{
static int i = 0;
int j;
if (visited[v] == 0)
{
if (i == 0) //首个
cout << v;
else
cout << " " << v;
i++;
visited[v] = 1;
}
for (j = 1; j <= g.n; j++) //遍历该层
if (g.edges[v][j] && visited[j] == 0)
DFS(g, j);
}
- 用邻接表表示
void DFS(AdjGraph* G, int v)
{
static int n = 0;
ArcNode* p;
visited[v] = 1;
if (!n)
{
cout << v;
n++;
}
else
{
cout << " " << v;
n++;
}
p = G->adjlist[v].firstarc;
while (p != NULL)
{
if (visited[p->adjvex] == 0)
DFS(G, p->adjvex);
p = p->nextarc;
}
}
1.3.2 广度遍历(BFS)
- 用邻接矩阵表示
#include <queue>
void BFS(MGraph g, int v)//广度遍历
{
int temp, j;
queue<int>q;
if (visited[v] == 0)
{
cout << v;
visited[v] = 1;
q.push(v);
}
while (!q.empty())
{
temp = q.front();
q.pop();
for (j = 1; j <= g.n; j++) ////遍历该层
{
if (g.edges[temp][j] == 1 && visited[j] == 0)
{
cout << " " << j;
visited[j] = 1;
q.push(j);
}
}
}
}
- 用邻接表表示
void BFS(AdjGraph* G, int v)
{
int w, i;ArcNode* p;
queue<int>q;
cout << v;
visited[v] = 1;
q.push(v);
while (!q.empty())
{
w = q.front();
q.pop();
p = G->adjlist[w].firstarc;
while (p != NULL)
{
if (visited[p->adjvex] == 0)
{
cout << " " << p->adjvex;
visited[p->adjvex] = 1;
q.push(p->adjvex);
}
p = p->nextarc;
}
}
}
-
应用:图着色问题

代码实现
#define MAXV 600
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include<queue>
#include<map>
using namespace std;
typedef struct ANode
{
int adjvex; //该边的终点编号
struct ANode* nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{
Vertex data; //顶点信息
ArcNode* firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct
{
AdjList adjlist; //邻接表
int v, e; //图中顶点数v和边数e
} AdjGraph;
int visited[MAXV];
int flag = 0;
void CreateAdj(AdjGraph*& G, int v, int e); //创建图邻接表
int CheckK(int color[MAXV], int v, int k); //检查color是否符合K值
int BFS(AdjGraph* G, int v, int color[MAXV]);//广度遍历
int main()
{
AdjGraph* G;
int v, e, k, n, i, j;
int color[MAXV];
cin >> v >> e >> k;
CreateAdj(G, v, e);
cin >> n;
for (i = 1; i <= n; i++)
{
for (j = 1; j <= v; j++)
{
cin >> color[j];
visited[j] = 0;
}
if (CheckK(color, v, k))
{
if (BFS(G, v, color)) //传入的应该时是v,不是1
cout << "Yes" << endl;
else
cout << "No" << endl;
}
else
cout << "No" << endl;
}
return 0;
}
void CreateAdj(AdjGraph*& G, int v, int e)
{
int i;
G = new AdjGraph;
G->e = e;
G->v = v;
for (i = 1; i <= v; i++)
G->adjlist[i].firstarc = NULL;
for (i = 1; i <= e; i++)
{
int a, b;
cin >> a >> b;
ArcNode* p, * q;
p = new ArcNode;
q = new ArcNode;
p->adjvex = b;
q->adjvex = a;
p->nextarc = G->adjlist[a].firstarc;
G->adjlist[a].firstarc = p;
q->nextarc = G->adjlist[b].firstarc;
G->adjlist[b].firstarc = q;
}
}
int CheckK(int color[MAXV], int v, int k) //检查color是否符合K值
{
int i;
map<int, int> mp;
for (i = 1; i <= v; i++)
mp[color[i]] = 1;
if (mp.size() != k)
return 0;
else
return 1;
}
int BFS(AdjGraph* G, int v, int color[MAXV])
{
int w, i, temp;
ArcNode* p;
queue<int>q;
visited[v] = 1;
q.push(v);
while (!q.empty())
{
w = q.front();
temp = color[w];
q.pop();
p = G->adjlist[w].firstarc;
while (p != NULL)
{
if (visited[p->adjvex] == 0) //仍要进行检查该顶点是否遍历过,未遍历顶点方可入队
{
visited[p->adjvex] = 1;
q.push(p->adjvex);
}
if (temp == color[p->adjvex])
return 0;
visited[p->adjvex] = 1;
p = p->nextarc;
}
}
for (i = 1; i <= v; i++) //检查是否有不相通的图
{
if (visited[i] == 0)
{
visited[i] = 1;
q.push(i);
while (!q.empty())
{
w = q.front();
temp = color[w];
q.pop();
p = G->adjlist[w].firstarc;
while (p != NULL)
{
if (visited[p->adjvex] == 0) //仍要进行检查该顶点是否遍历过,未遍历顶点方可入队
{
visited[p->adjvex] = 1;
q.push(p->adjvex);
}
if (temp == color[p->adjvex])
return 0;
visited[p->adjvex] = 1;
p = p->nextarc;
}
}
}
}
return 1;
}
1.4 最小生成树
-
介绍:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树,如下图:
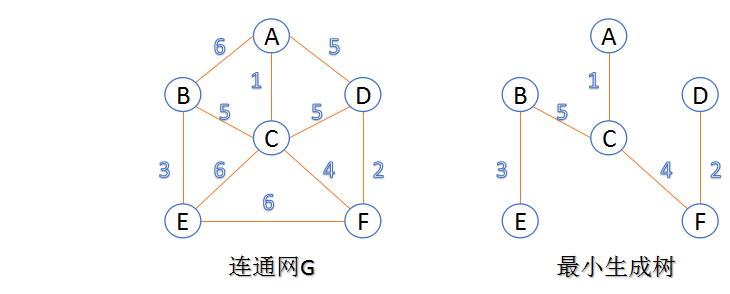
1.4.1 Prim算法
-
介绍:从起点开始,先选择与起点相连且代价最小的边的对应顶点加入最小生成树,之后将选中的顶点们视为整体,继续寻找与该整体相连且代价最小的边的对应顶点,直到最小生成树
有n-1条边或者n个顶点为止。
-
图解
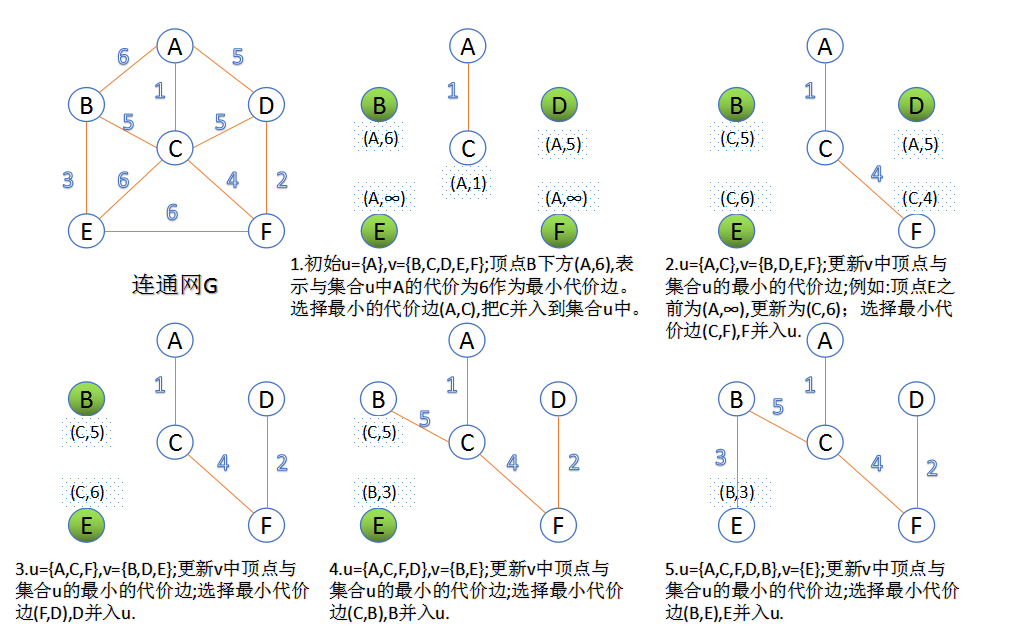
-
代码实现
void Prim()
{
int i, min, j, mark=-1, sum = 0;
for (i = 1; i <= n; i++)//赋初值,即将closest数组都赋为第一个节点v,lowcost数组赋为第一个节点v到各节点的权重
lowcost[i] = edges[1][i];//g.edges[v][i]的值指的是节点v到i节点的权重
lowcost[1] = 0;
for (i = 1; i < n; i++)//接下来找剩下的n-1个节点(g.n是图的节点个数)
{
min = INF;
for (j = 1; j <= n; j++)//遍历所有节点
{
if (lowcost[j] != 0 && lowcost[j] < min)//若该节点还未被选且权值小于之前遍历所得到的最小值
{
min = lowcost[j];//更新min的值
mark = j;//记录当前最小权重的节点的编号
}
}
sum = sum + min;
lowcost[mark] = 0;//表明k节点已被选了(作标记)
for (j = 1; j <= n; j++)//遍历所有节点
if (edges[mark][j] < lowcost[j])
lowcost[j] = edges[mark][j];//更新权重,使其当前最小
}
for (j = 1; j <= n; j++)
if (lowcost[j] != 0)
break;
if (j <= n)
{
cout << -1 << endl;
return;
}
cout << sum<<endl;
}
-
应用:公路村村通

代码实现:
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include<map>
#define MAXV 1001
#define INF 32767//表示无穷大
using namespace std;
int lowcost[MAXV];
int edges[MAXV][MAXV];
int n, e;
void CreateMGraph();//建图
void Prim();
int main()
{
cin >> n >> e;
if (e < n - 1)
cout << -1 << endl;
else
{
CreateMGraph();
Prim();
}
return 0;
}
void CreateMGraph()//建图
{
int i, j, a, b, c;
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
edges[i][j] = INF; //初始化邻接矩阵
for (i = 1; i <= e; i++)
{
cin >> a >> b >> c;
edges[a][b] = c;
edges[b][a] = c;
}
}
void Prim()
{
int i, min, j, mark=-1, sum = 0;
for (i = 1; i <= n; i++)//赋初值,即将closest数组都赋为第一个节点v,lowcost数组赋为第一个节点v到各节点的权重
lowcost[i] = edges[1][i];//g.edges[v][i]的值指的是节点v到i节点的权重
lowcost[1] = 0;
for (i = 1; i < n; i++)//接下来找剩下的n-1个节点(g.n是图的节点个数)
{
min = INF;
for (j = 1; j <= n; j++)//遍历所有节点
{
if (lowcost[j] != 0 && lowcost[j] < min)//若该节点还未被选且权值小于之前遍历所得到的最小值
{
min = lowcost[j];//更新min的值
mark = j;//记录当前最小权重的节点的编号
}
}
sum = sum + min;
lowcost[mark] = 0;//表明k节点已被选了(作标记)
for (j = 1; j <= n; j++)//遍历所有节点
if (edges[mark][j] < lowcost[j])
lowcost[j] = edges[mark][j];//更新权重,使其当前最小
}
for (j = 1; j <= n; j++)
if (lowcost[j] != 0)
break;
if (j <= n)
{
cout << -1 << endl;
return;
}
cout << sum<<endl;
}
1.4.2 Kruskal算法
-
介绍:按权值从小到大选择边,所选的边所连接的两个顶点应属于两颗不同的树,然后将这两个顶点合并至同一树,重复操作,直到所有顶点都在一颗树内或者有n-1条边为止。
-
图解
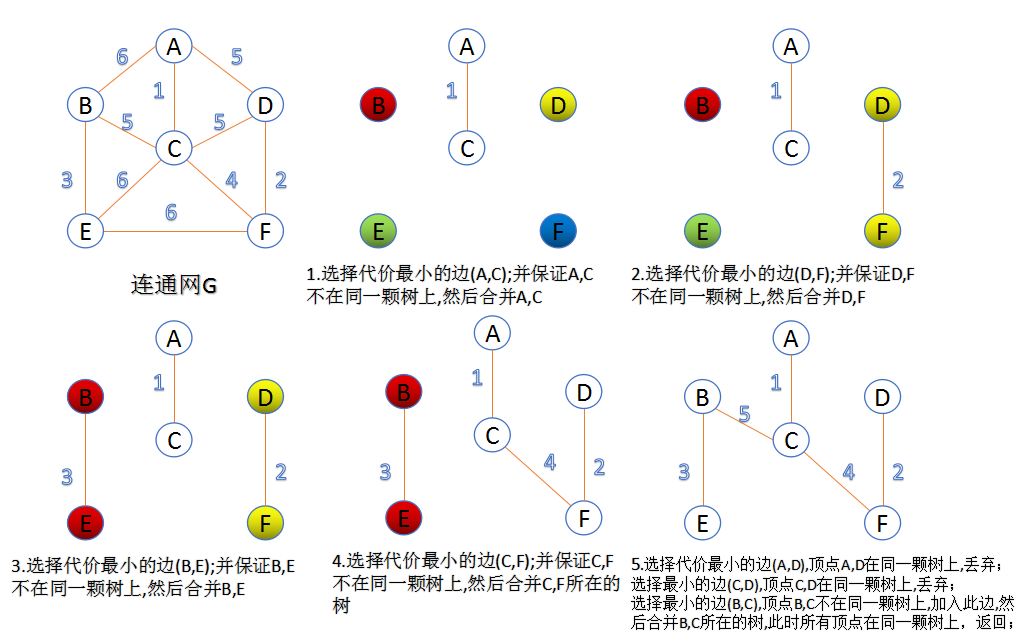
-
代码实现
#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
const int M = 1e5+7;
struct node
{
int a,b,val;
} Q[M];
int fa[M];
int Rd()
{
int res=0;char c;
while(c=getchar(),!isdigit(c));
do {
res=(res<<3)+(res<<1)+(c^48);
} while(c=getchar(),isdigit(c));
return res;
}
bool cmp(LZ a,LZ b){
return a.val<b.val;
}
int getfa(int v){
if(fa[v]!=v)fa[v]=getfa(fa[v]);
return fa[v];
}
int main()
{
int i,j,n,m,x,y;
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++)
{
Q[i].a=Rd();Q[i].b=Rd();Q[i].val=Rd();
}
sort(Q+1,Q+m+1,cmp);
for(i=1;i<=n;i++)
{
fa[i]=i;
}
int sum=0,cut=0;
for(i=1;i<=m;i++)
{
x=getfa(Q[i].a);
y=getfa(Q[i].b);
if(x==y)continue;
sum+=Q[i].val;
if(++cut==n-1)break;
fa[x]=y;
}
printf("%d",sum);
return 0;
}
1.5 最短路径
- 介绍:求出从有向图中某一顶点到另一顶点的路径中其权值之和最小的路径。
1.5.1 Dijkstra算法
-
图解
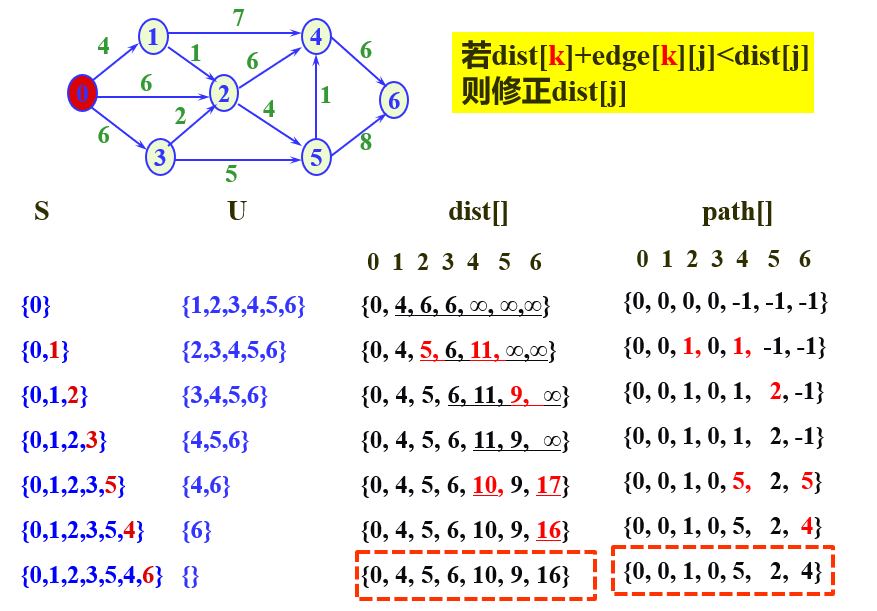
-
相关知识点:
1.dist[i]表示起点到i顶点的路径。
2.g.edges[i][j]表示顶点i到顶点[j]的路径。
3.path[j]表示j顶点的前驱顶点。
-
代码实现
void Dijkstra(MGraph g, int v) //源点v到其他顶点最短路径
{
int dist[MAXV], path[MAXV], visited[MAXV];
int min = INF, i, j, mark;
for (i = 0; i < g.n; i++) //初始化dist和cost
{
dist[i] = g.edges[v][i];
if (g.edges[v][i] < INF)
path[i] = v;
else
path[i] = -1;
visited[i] = 0;
}
visited[v] = 1;
while (1) //遍历路径矩阵
{
min = INF;
for (j = 0; j < g.n; j++) //找最小
{
if (!visited[j] && (dist[j] <= min))
{
mark = j;
min = dist[j];
}
}
if (min == INF)
break;
visited[mark] = 1;
for (j = 0; j < g.n; j++)
{
if (!visited[j])
{
if (dist[mark] + g.edges[mark][j] < dist[j]) //以最短路径为优先条件
{
dist[j] = dist[mark] + g.edges[mark][j];
path[j] = mark;
}
}
}
}
Dispath(dist, path, visited, g.n, v);
}
-
应用:旅游规划

代码实现:
#include <iostream>
#define MAXV 505
#define INF 32767//表示无穷大
using namespace std;
typedef struct //图的定义
{
int n, e; //顶点数,弧数
int road[MAXV][MAXV];//表示路径
int cost[MAXV][MAXV];//表示花费
} MGraph; //图的邻接矩阵表示类型
int dist[MAXV], cost[MAXV], visited[MAXV];
MGraph g;
void CreateMGraph();//建图
void Dijkstra(int S, int D);
int main()
{
int N, M, S, D;
cin >> N >> M >> S >> D;
g.n = N;
g.e = M;
CreateMGraph();
Dijkstra(S, D);
return 0;
}
void CreateMGraph()//建图
{
int i, j, a, b, length, price;
for (i = 0; i < g.n; i++) //初始化两个邻接矩阵
{
for (j = 0; j < g.n; j++)
{
g.road[i][j] = INF;
g.cost[i][j] = INF;
g.cost[i][i] = 0;
g.road[i][i] = 0;
}
}
for (i = 0; i < g.e; i++) //输入数据
{
cin >> a >> b >> length >> price;
g.road[a][b] = g.road[b][a] = length;
g.cost[a][b] = g.cost[b][a] = price;
}
}
void Dijkstra(int S, int D)
{
int i, j, min = INF, mark;
for (i = 0; i < g.n; i++) //初始化dist和cost
{
dist[i] = g.road[S][i];
cost[i] = g.cost[S][i];
visited[i] = 0;
}
visited[S] = 1;
while (1) //遍历路径矩阵
{
min = INF;
for (j = 0; j < g.n; j++) //找最小
{
if (!visited[j] && (dist[j] <= min))
{
mark = j;
min = dist[j];
}
}
if (min == INF)
break;
visited[mark] = 1;
for (j = 0; j < g.n; j++)
{
if (!visited[j] && g.road[mark][j] < INF)
{
if (dist[mark] + g.road[mark][j] < dist[j]) //以最短路径为优先条件
{
dist[j] = dist[mark] + g.road[mark][j];
cost[j] = cost[mark] + g.cost[mark][j]; //花费也应及时更新
}
else if (dist[mark] + g.road[mark][j] == dist[j] && cost[mark] + g.cost[mark][j] < cost[j]) //若路径相同,比较花费
cost[j] = cost[mark] + g.cost[mark][j];
}
}
}
cout << dist[D] << " " << cost[D] << endl;
}
1.5.2 Floyd算法
-
图解
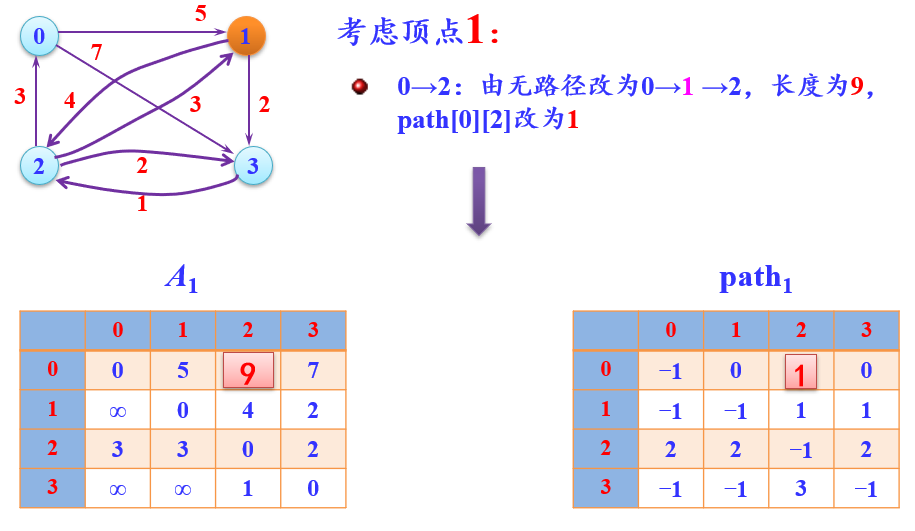


-
代码实现
#include<stdio.h>
#include<stdlib.h>
#define max 1000000000
int d[1000][1000],path[1000][1000];
int main()
{
int i,j,k,m,n;
int x,y,z;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++){
d[i][j]=max;
path[i][j]=j;
}
for(i=1;i<=m;i++) {
scanf("%d%d%d",&x,&y,&z);
d[x][y]=z;
d[y][x]=z;
}
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++) {
if(d[i][k]+d[k][j]<d[i][j]) {
d[i][j]=d[i][k]+d[k][j];
path[i][j]=path[i][k];
}
}
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
if (i!=j) printf("%d->%d:%d\n",i,j,d[i][j]);
int f, en;
scanf("%d%d",&f,&en);
while (f!=en) {
printf("%d->",f);
f=path[f][en];
}
printf("%d\n",en);
return 0;
}
-
Dijkstra与Floyd算法的比较
1.Floyd算法适合稠密图且边权可正可负,但时间复杂度比较高(O(n^3)),不适合计算大量数据。
2.Dijkstra算法权值不能为负,且不能求最长路径。
1.6 拓扑排序
-
介绍:只针对有向无环图进行操作,将该图中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。
-
图解
从D图中找到一个没有前驱的顶点输出,然后删除以这个点为起点的边,重复以上操作,直到最后一个顶点被输出。如果还有顶点未被输出,则说明有环。
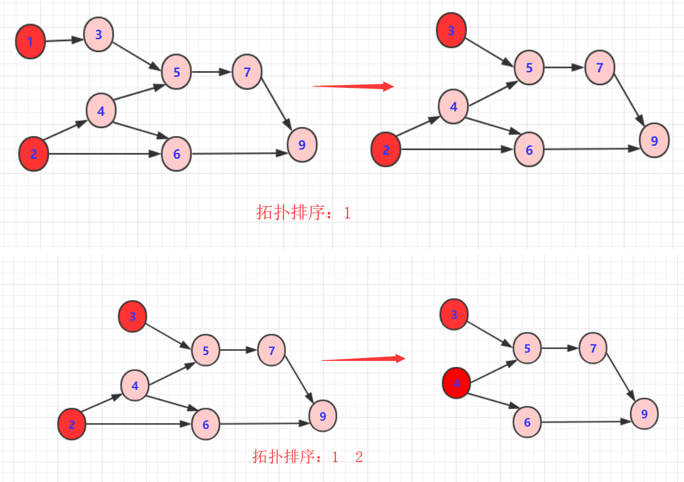
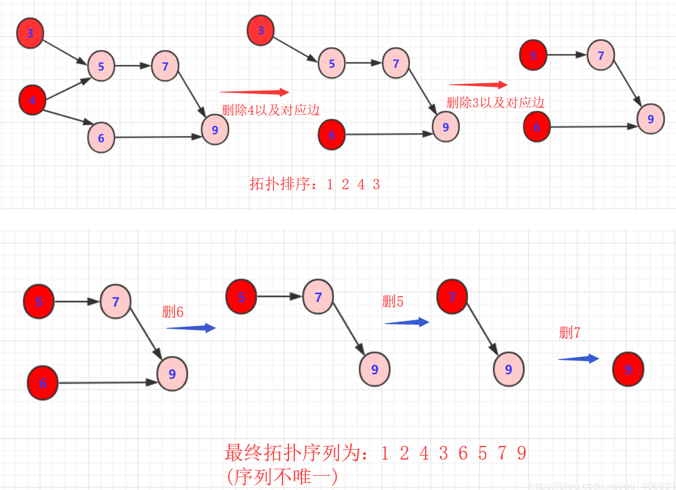
-
代码实现
void TopSort(AdjGraph *G)//邻接表拓扑排序
{
int i, j, k=-1, cnt=0;
int St[MAXV], top=-1, a[MAXV]; //栈St的指针为top
ArcNode *p;
for(i=0; i<G->n; i++)
G->adjlist[i].count = 0; //入度置初值为0
for(i=0; i<G->n; i++) //求所有顶点的入度
{
p = G->adjlist[i].firstarc;
while(p!=NULL)
{
G->adjlist[p->adjvex].count++;
p = p->nextarc;
}
}
for(i=0; i<G->n; i++)
{
if(G->adjlist[i].count==0) //入度为0的顶点进栈
{
top++;
St[top] = i;
}
}
while(top>-1) //栈不为空时循环
{
i = St[top]; //出栈
top--;
a[++k] = i;
p = G->adjlist[i].firstarc; //找第一个相邻的顶点
cnt++;
while(p!=NULL)
{
j = p->adjvex;
G->adjlist[j].count--;
if(G->adjlist[j].count==0) //入度为0的相邻顶点入栈
{
top++;
St[top] = j;
}
p = p->nextarc; //找下一个相邻顶点
}
}
if(cnt!=G->n)
{
printf("error!");
return;
}
j=0;
printf("%d", a[j]);
for(j=1; j<=k; j++)
printf(" %d", a[j]);
}
1.7 关键路径
-
AOE网:用一个带权有向图描述工程的预计进度。顶点表示事件,有向边表示活动,边的权表示完成活动e所需的时间。图中入度为0的顶点表示工程的开始事件,出度为0的顶点表示工程
结束事件。
-
关键路径:从AOE网中源点到汇点的最长路径,具有最大长度的路径叫关键路径。关键路径是由关键活动构成的,关键路径可能不唯一。
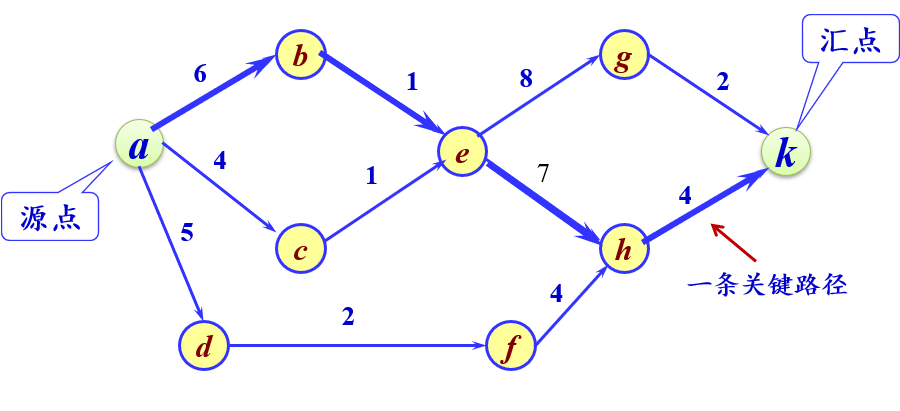
-
最早开始时间和最迟开始时间:活动a的最早开始时间e(a)指该活动起点x事件的最早开始时间,即:e(a)=ee(x);活动a的最迟开始时间l(a)指该活动终点y事件的最迟开始时间与该活动
所需时间之差,即:l(a)=le(y)-c。

-
关键活动:对于每个活动a,求出d(a)=l(a)-e(a),若d(a)为0,则称活动a为关键活动。
1.8 对图的认识及学习体会
在图这一方面,光看预习课件是远远不够的,还要结合编程来加深对知识点的理解。举个例子,我第一次看邻接表的结构体定义时人直接傻了,头一次看见这么多的结构体套来套去的,后来还
是通过PTA一边摸索一边理解,还有就是邻接矩阵的长度问题,在PTA上有一些题目把图的边长跟顶点数据搞得很大,虽然可以在程序里把邻接矩阵设为全局变量以避免超栈错误,但终究是权
宜之计,还是要继续专研,寻找更好的方法。
2.阅读代码
2.1 题目及解题代码
-
题目:

-
解题代码
class Solution {
public:
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
vector<vector<int>> res;
vector<bool> visit(graph.size(),false);
dfs(res,0,graph,{},visit);
return res;
}
void dfs(vector<vector<int>>& res,int start,vector<vector<int>>& graph,vector<int> temp,vector<bool>visit){
if(graph[start].size() == 0 || temp.size()>=graph.size()){
res.push_back(temp);
return;
}
if(visit[start]== false)
temp.push_back(start);
//visit[start] = true;
for(int i = 0;i < graph[start].size();i++){
if(visit[graph[start][i]])
continue;
else{
temp.push_back(graph[start][i]);
visit[graph[start][i]] = true;
dfs(res,graph[start][i],graph,temp,visit);
temp.pop_back();
visit[graph[start][i]] = false;
}
}
}
};
2.1.1 该题的设计思路
-
思路:temp用于存储每一种可能的路(即每次只存一条路),res用于存储每一个temp(即有几种可能的路就存几次temp),用深度遍历实现即可。
-
时间复杂度:O(e),e表示顶点数。
-
空间复杂度:跟进了全图,所以为O(e),e表示顶点数。
2.1.2 该题的伪代码
void dfs(vector<vector<int>>& res,int start,vector<vector<int>>& graph,vector<int> temp,vector<bool>visit){
if 起始顶点无出度或temp的长度大于等于图的总顶点数 then
temp进入res
return;
end if
if 该顶点被被标记为false
该顶点进入temp
遍历该顶点的所有邻接点
if visit[graph[start][i]] then
continue;
else
邻接点进入temp并标记为true;
邻接点、temp进入dfs递归
删除temp的最后一个元素
邻接点标记为false;
end if
}
2.1.3 运行结果
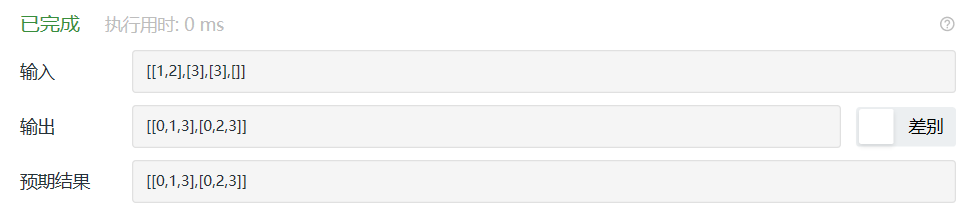
2.1.4分析该题目解题优势及难点
-
优势:思路缜密,用vector<vector
>存储多种路径是一大亮点。 -
难点:如何快速简单地存储多种可能路径是一大难点。
2.2 题目及解题代码
- 题目

- 解题代码
class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> inDegree(numCourses, 0); // 记录Node的入度
vector<vector<int>> adjLst(numCourses, vector<int>()); // 邻接表
for(auto arr : prerequisites) {
inDegree[arr[0]]++; // 更新 入度及其邻接表adjTable
adjLst[arr[1]].push_back(arr[0]);
}
queue<int> que; // topo排序依赖的队列
for(auto cnt=0;cnt<inDegree.size();cnt++) {
if(inDegree[cnt]==0) que.push(cnt);
}
vector<int> res;
while(!que.empty()) {
auto tmp = que.front(); que.pop();
// cout<< tmp << endl;
res.push_back(tmp); // 拓扑排序
for(auto i : adjLst[tmp]) { // 更新排序节点的连通nodes的入度
if(--inDegree[i]==0) que.push(i);
}
}
if(res.size() == numCourses) return res;
else return {} ;
}
};
2.2.1 该题的设计思路
-
思路:采用拓扑排序思想,每次从入度为 0 的结点开始,加入队列,并把这个结点指向的结点的入度 -1 。之后再把新的入度为 0 的结点加入队列。如果队列都处理完毕,但是和总结点数
不符,说明有些结点形成环。
-
时间复杂度:O(n),n表示输入的课程数量。
-
空间复杂度:O(n)。
2.2.2 该题的伪代码
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> inDegree(numCourses, 0); // 记录Node的入度
vector<vector<int>> adjLst(numCourses, vector<int>()); // 邻接表
queue<int> que; // topo排序依赖的队列
vector<int> res; //拓扑排序后所得的数据
遍历数据,录入邻接表adjTable并记录各结点的入度
遍历各结点,若入度为0则该结点入队
while 队不空
设tmp取队首元素并执行出队操作
tmp进入res
遍历与tmp结点有连接的结点
if 该结点的入度减一后为0入队 then
que.push(i);
end if
end while
if res长度与输入的课程数量相同 then
return res;
else return {} ;
endif
}
2.2.3 运行结果
2.2.4分析该题目解题优势及难点
-
优势:思路清晰,简单易懂,用了vector<vector
>来定义邻接表,值得学习,用res的最终长度判断是否能完成所有课程大大节省了运行时间。 -
难点:学会拓扑排序思想解决本题就不难。
2.3 题目及解题代码
-
题目
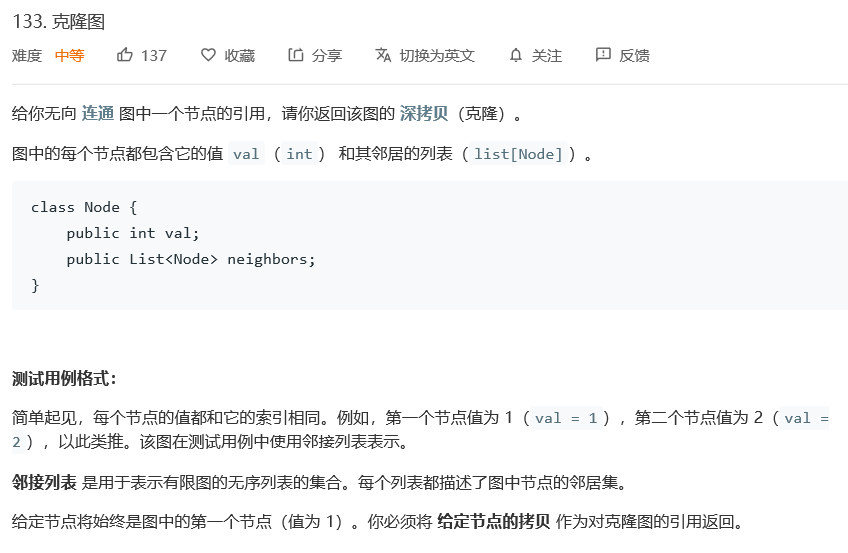
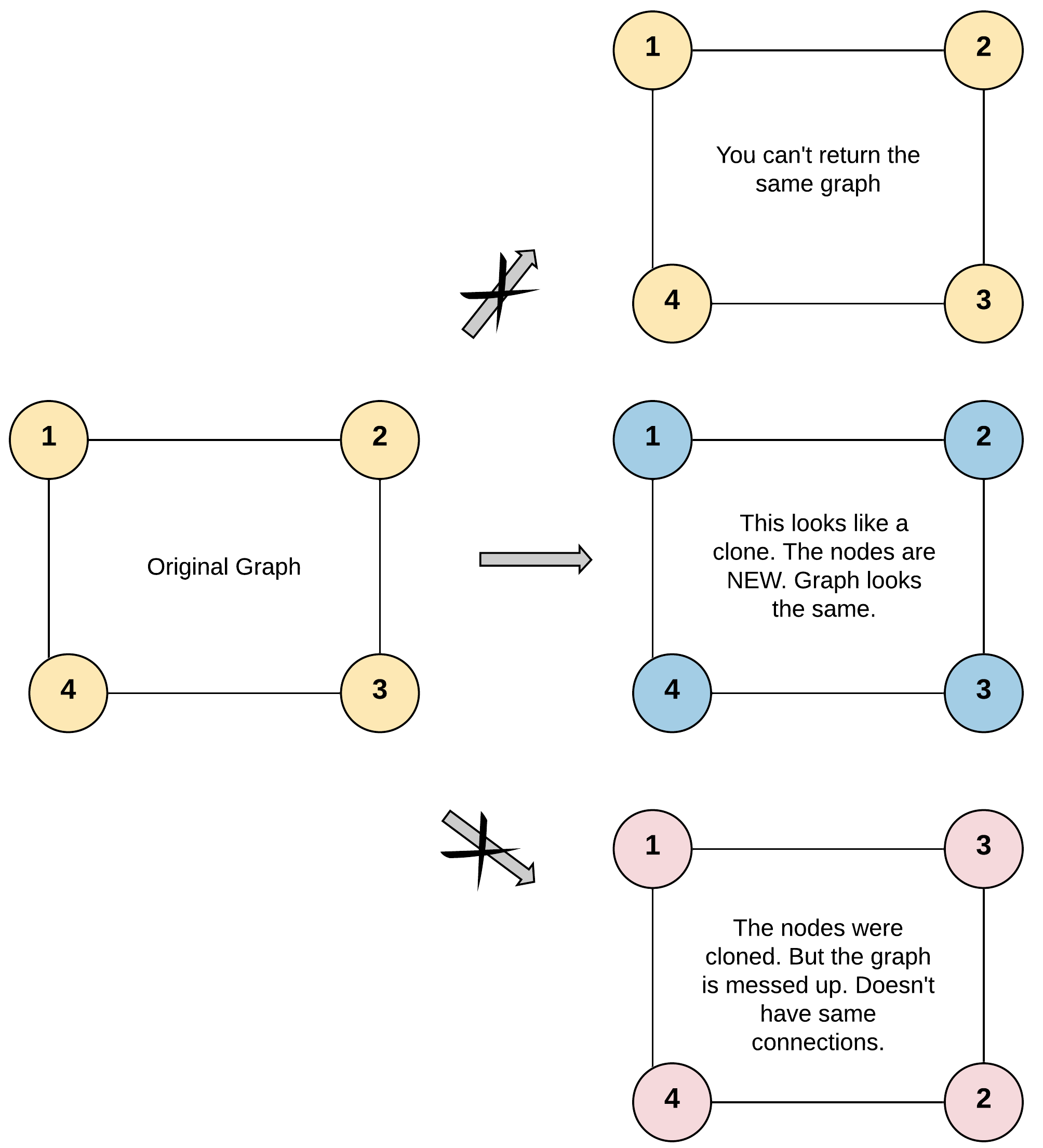

-
解题代码
struct Node** visited;
struct Node* dfs(struct Node* s){
if(s == NULL){
return NULL;
}
if(visited[s->val]){
return visited[s->val];
}
int i;
struct Node* nd = (struct Node*)malloc(sizeof(struct Node));
nd->val = s->val;
nd->numNeighbors = s->numNeighbors;
visited[nd->val] = nd;
nd->neighbors = (struct Node**)malloc(sizeof(struct Node*)*nd->numNeighbors);
for(i = 0; i < nd->numNeighbors; i++){
nd->neighbors[i] = dfs(s->neighbors[i]);
}
return nd;
}
struct Node *cloneGraph(struct Node *s) {
visited = (struct Node**)malloc(sizeof(struct Node*)*101);
memset(visited, 0, sizeof(struct Node*)*101);
return dfs(s);
}
2.3.1 该题的设计思路
-
思路:预先定义一个结点指针数组的全局变量visited用于存储全部结点地址,顺便用于判断该节点是否被访问过,然后深度遍历原图完成复制即可。
-
时间复杂度:O(e),e表示顶点数。
-
空间复杂度:跟进了全图,所以为O(e),e表示顶点数。
2.3.2 该题的伪代码
struct Node** visited;
struct Node* dfs(struct Node* s){
if s为空 then
return NULL;
end if
if 该顶点有标记 then
return visited[s->val];
end if
int i;
申请一个结构体nd
将原图顶点的编号、邻居数量赋予nd
把nd复制在在visited的对应位置(即完成标记)
申请nd邻居的空间
for i = 0 to i < nd->numNeighbors
nd->neighbors[i] = dfs(s->neighbors[i]);
end for
返回nd
}
struct Node *cloneGraph(struct Node *s) {
visited = (struct Node**)malloc(sizeof(struct Node*)*101);
memset(visited, 0, sizeof(struct Node*)*101);
//visited = (struct Node **)calloc(101, sizeof(struct Node*));
//calloc初始化时会自动清理内存,malloc初始化完事后内存空间内为随机数据。
return dfs(s);
}
2.3.3 运行结果
2.3.4分析该题目解题优势及难点
-
优势:将原本只是用于检查是否遍历过的visited数组的功能进一步拓展成可以存储全部顶点,乘深度遍历之机先将原图所有顶点置于visited之中,然后再以递归的形式赋予nd即可。
-
难点:图中一个节点可以拥有任意数量的邻接点。在复制时很可能陷入死循环,因此需要提前了解图的结构并以某种方式跟踪已经复制的节点。



