1. 哈夫曼树的基本概念
哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。
所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的带权路径长度记为:
WPL=(W1*L1+W2*L2+W3*L3+...+ Wn*Ln)
N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。
可以证明哈夫曼树的WPL是最小的。
为了直观其见,下图中把带权的叶子结点画成方形,其他非叶子结点仍为圆形。请看下图中的三棵二叉树以及它们的带权路径长:
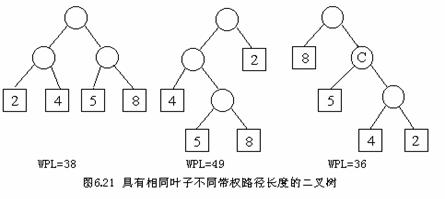
注意:这三棵二叉树叶子结点数相同,它们的权值也相同,但是它们的 WPL带权路径长各不相同。图(c)WPL最小。它就是哈曼树,即最优树。
2. 哈夫曼树的构造
构造哈夫曼树的方法
对于已知的一组叶子的权值W 1 ,W 2...... ,W n
①首先把 n 个叶子结点看做 n 棵树(仅有一个结点的二叉树),把它们看做一个森林。
②在森林中把权值最小和次小的两棵树合并成一棵树,该树根结点的权值是两棵子树权值之和。这时森林中还有 n-1 棵树。
③重复第②步直到森林中只有一棵为止,此树就是哈夫曼树。
现给一组 (n=4) 具体的权值: 2 , 4 , 5 , 8 ,下边是构造具体过程:
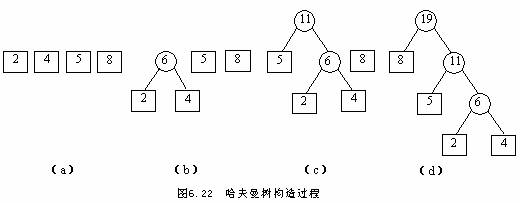
n 个叶子构成的哈夫曼树其带权路径长度是唯一的,但树形是不唯一的。因为将森林中两棵权值最小和次小的子棵合并时,哪棵做左子树,哪棵做右子树并不严格限制。
3. 哈夫曼树的应用
在通信及数据传输中多采用二进制编码。为了使电文尽可能的缩短,可以对电文中每个字符出现的次数进行统计。设法让出现次数多的字符的二进制码短些,而让那些很少出现的字符的二进制码长一些。
假设有一段电文,其中用到 4 个不同字符A, C, S, T,它们在电文中出现的次数分别为 8 , 2 , 4 , 5 。把 8, 2 , 4 , 5 当做 4 个叶子的权值构造哈夫曼树如下图所示。在树中令所有左分支取编码为 0 ,令所有右分支取编码为1。将从根结点起到某个叶子结点路径上的各左、右分支的编码顺序排列,就得这个叶子结点所代表的字符的二进制编码,j结果如下图所示。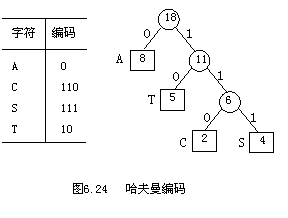
这些编码拼成的电文不会混淆,因为每个字符的编码均不是其他编码的前缀,这种编码称做前缀编码。关于信息编码是一个复杂的问题,还应考虑其他一些因素。比如前缀编码每个编码的长度不相等,译码时较困难。还有检测、纠错问题都应考虑在内。这里仅对哈夫曼树举了一个应用实例。


