自学python笔记（二）

⏰前言

不知不觉今天已经过去大半，本以为昨天就能更新的文章今天的这个时候才开始码字。今天总结两个项目：猜数字和预测概率。编程可以让人明白一些道理，甚至让你觉得看似不相关的随机数其实也是有被预测的可能，那么接下来就来玩一玩这两组代码吧！

😝猜数字

假设Joe的年龄是18岁，她被询问年龄时不想直接做出直接的回答，但出于礼貌又有必要告诉对方，于是Joe想写一个程序，通过给出提示让别人猜测。这里就要用到while语句来构造这样一个程序。

joe_age = 18
guess = int(input(">>:"))
while guess != joe_age:
    if guess > joe_age:
        print("猜的太大了，往小试试……")
    elif guess < joe_age:
        print("猜的太小了，往大试试……")
    guess = int(input(">>:"))
print("恭喜你，猜对了！")

while循环不同于for循环就在于它可以无限循环，我们不能知道要猜多少次，所以while循环更加适合这样的场景。

guess = int(input(">>:"))

同时也用到if和elif条件判断语句：

if guess > joe_age:
        print("猜的太大了，往小试试……")
    elif guess < joe_age:
        print("猜的太小了，往大试试……")
    guess = int(input(">>:"))
print("恭喜你，猜对了！")

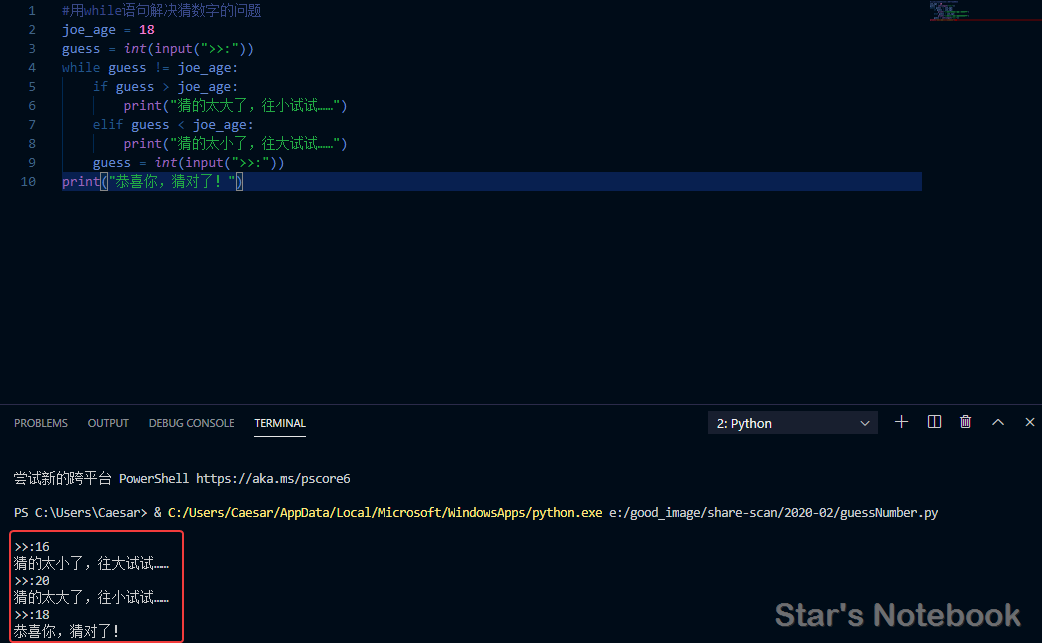
当猜测年龄大于实际年龄，打印“猜的太大了，往小试试……”，当猜测年龄小于实际年龄，打印“猜的太小了，往大试试……”，当猜测年龄等于实际年龄，打印"恭喜你，猜对了！"程序运行结果如下图所示：

🏆获胜概率预测

场景如下：
1.小A和小B羽毛球比赛，小A每球获胜概率55%，小B每球获胜概率45%；
2.每局比赛，先得21分者获胜；
3.假设进行10000局比赛，两人分别会获胜多少局？
首先构造顶层框架：

def main():
    #主要逻辑
    prob_A, prob_B, number_of_games = get inputs() #获取原始数据
    win_A, win_B = sim_n_games(prob_A, prob_B, number_of_games) #获取模拟结果
    print_summary(win_A, win_B, number_of_games) #结果汇总输出

def main()定义函数main, prob_A小A每球获胜概率,prob_B小B每球获胜概率,number_of_games比赛场数。通过以上参数，再获得两人分别赢多少局 win_A, win_B。最后进行汇总输出print_summary。

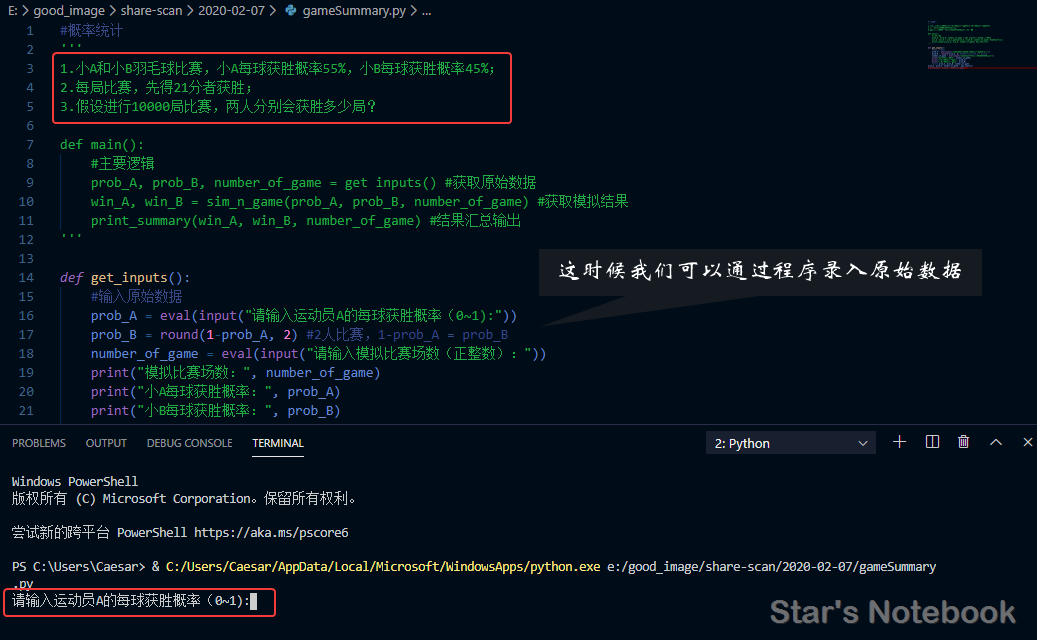
录入原始数据

def get_inputs():
    #输入原始数据
    prob_A = eval(input("请输入运动员A的每球获胜概率（0~1):"))
    prob_B = round(1-prob_A, 2) #2人比赛，1-prob_A = prob_B
    number_of_games = eval(input("请输入模拟比赛场数（正整数）："))
    print("模拟比赛场数：", number_of_games)
    print("小A每球获胜概率：", prob_A)
    print("小B每球获胜概率：", prob_B)
    return prob_A, prob_B, number_of_games #每一次return语句出现代表调用函数结束
prob_A, prob_B, number_of_games = get_inputs()
print(prob_A, prob_B, number_of_games)

多场比赛模拟

进行多场比赛模拟（ score_A, score_B是获得比分，其中一人到达 21循环停止：

def sim_n_games(prob_A, prob_B, number_of_games): #定义sim_n_games函数
    #模拟多场比赛的结果
    win_A, win_B = 0, 0 #初始化A和B获胜的场次
    for i in range(number_of_games): #迭代number_of_games次,以下是模拟一场比赛，for循环一万次
        score_A, score_B = sim_one_game(prob_A, prob_B) #获得模拟比赛的比分 
        if score_A > score_B:
            win_A +=1
        else:
            win_B +=1
    return win_A, win_B

单次比赛情况模拟

然后我们再进行简化，把多场比赛简化成模拟一场比赛，再进行10000次循环：

import random
def sim_one_game(prob_A, prob_B):
    #模拟一场比赛的结果
    score_A, score_B = 0,0
    while not game_over(score_A, score_B): #这里用到while循环
        if random.random() < prob_A: 
            score_A +=1
        else :
            score_B +=1
    return score_A, score_B

注意上面代码中 if random.random() < prob_A: 随机数据小于小A每球获胜概率的55%，则A获胜一次，此处需要用心理解。

汇总输出

def print_summary(win_A, win_B, number_of_games):
    print("共模拟了{}场比赛" .format(number_of_games)) #模拟总场次
    print("选手A获胜{0}场，占比{1:.1%}" .format(win_A, win_A/number_of_games)) #A获胜的概率除以总场次乘以100%
    print("选手B获胜{0}场，占比{1:.1%}" .format(win_B, win_B/number_of_games)) #B获胜的概率除以总场次乘以100%

最终形成程序

import random


def get_inputs():
    #输入原始数据
    prob_A = eval(input("请输入运动员A的每球获胜概率（0~1):"))
    prob_B = round(1-prob_A, 2) #2人比赛，1-prob_A = prob_B
    number_of_games = eval(input("请输入模拟比赛场数（正整数）："))
    print("模拟比赛场数：", number_of_games)
    print("小A每球获胜概率：", prob_A)
    print("小B每球获胜概率：", prob_B)
    return prob_A, prob_B, number_of_games #每一次return语句出现代表调用函数结束
#prob_A, prob_B, number_of_games = get_inputs()
#print(prob_A, prob_B, number_of_games)


def game_over(score_A, score_B):
    #单场模拟结束条件是一方获得21分
    return score_A == 21 or score_B == 21


def sim_one_game(prob_A, prob_B):
    #模拟一场比赛的结果
    score_A, score_B = 0,0
    while not game_over(score_A, score_B):
        if random.random() < prob_A:
            score_A += 1
        else :
            score_B += 1
    return score_A, score_B


def sim_n_games(prob_A, prob_B, number_of_games): #定义sim_n_games函数
    #模拟多场比赛的结果
    win_A, win_B = 0, 0 #初始化A和B获胜的场次
    for i in range(number_of_games): #迭代number_of_games次,以下是模拟一场比赛，for循环一万次
        score_A, score_B = sim_one_game(prob_A, prob_B) #获得模拟比赛的比分 
        if score_A > score_B:
            win_A += 1
        else:
            win_B += 1
    return win_A, win_B


def print_summary(win_A, win_B, number_of_games):
    print("共模拟了{}场比赛" .format(number_of_games)) #模拟总场次
    print("选手A获胜{0}场，占比{1:.1%}" .format(win_A, win_A/number_of_games)) #A获胜的概率除以总场次乘以100%
    print("选手B获胜{0}场，占比{1:.1%}" .format(win_B, win_B/number_of_games)) #B获胜的概率除以总场次乘以100%


def main():
    #主要逻辑
    prob_A, prob_B, number_of_games = get_inputs() #获取原始数据
    win_A, win_B = sim_n_games(prob_A, prob_B, number_of_games) #获取模拟结果
    print_summary(win_A, win_B, number_of_games) #结果汇总输出


if __name__ == "__main__":
    main()

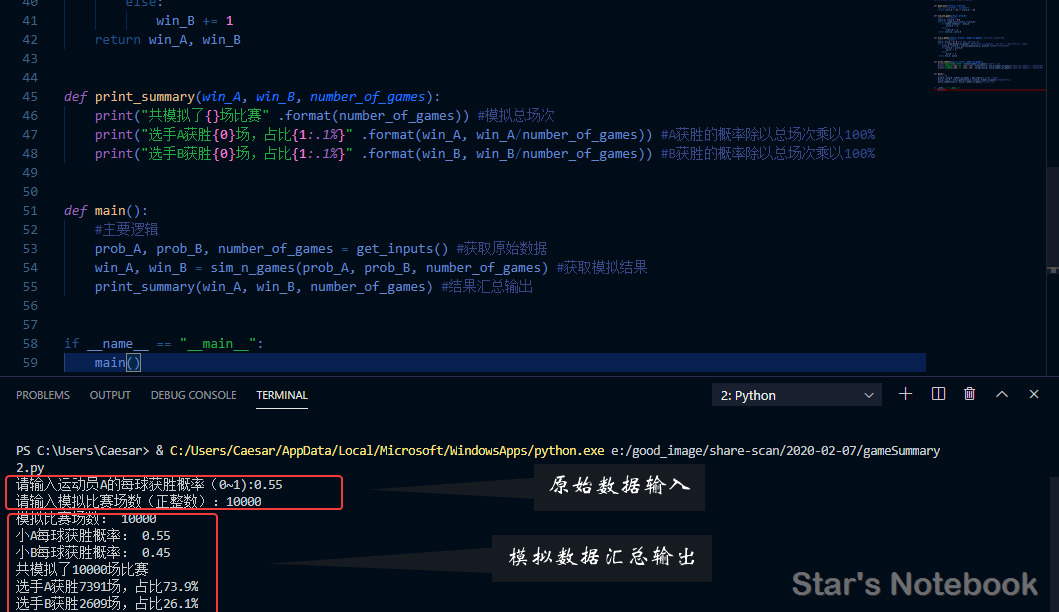
到此，整个程序运行完毕，代码中的注释部分需要认真阅读。

👍小结

两个小案例的练习，让我觉得真的是每一个简单的自动化执行背后都是无数的辛酸。社会大分工后让人们的专业越来越细，越来越专，普罗大众漫不经心地使用机器进行自动化高效工作，殊不知越是高效、便捷、傻瓜式的智能，说明背后越是有人付出时间和精力帮助你完成更多要考虑到的事情。极客万岁！另外，概率分析这个案例，单个球的输赢概率A和B相差无几，但多次比赛下来却出现惊人的差距，正所谓“失之毫厘，差之千里啊！”

下章再见！🙋‍♀️

未经沟通转载，将追究法律责任，请尊重原创劳动成果！