【题解】T156527 直角三角形
题目链接:T156527 直角三角形
审题
根据勾股定理,\(a^2 + b^2 == c^2\)。
当然,由于勾股定理不在小学数学考查的的范围内,我们需要对勾股定理进行一些证明,让小学生能够轻松地做出此题。
勾股定理的证明
赵爽弦图
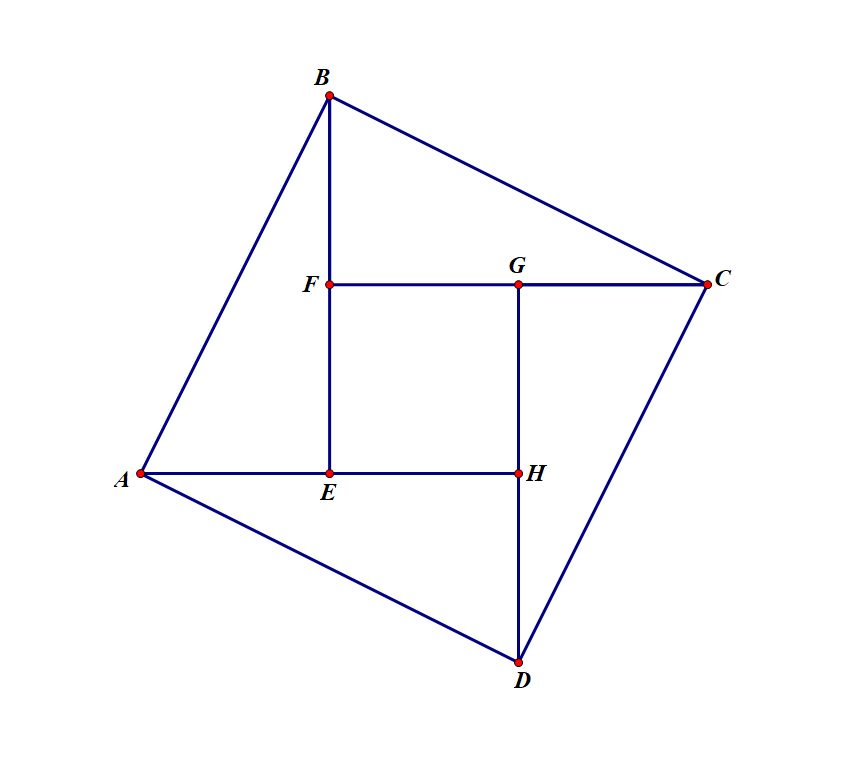
这个↑,就是传说中的“赵爽弦图”。
赵爽(?-?),一名婴,字君卿,是中国在三国时期吴国的数学家。生卒年不详,是否生活在三国时代其实也受质疑,著有《周髀算经注》,即对《周髀算经》的详细注释。
“勾股各自乘,并之,为弦实。开方除之,即弦。”
——赵爽《勾股圆方图说》
“按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实,亦成弦实。”
——赵爽《勾股圆方图说》
语文好的同学,可以直接看下一个证明方法了。
在这张途中,正方形ABDE以弦为边长,由4个相等的直角三角形再加上中间的那个小正方形组成。
不妨设 \(AE = BF = CG = DH = a\),\(BE = CF = DG = AH = b\),\(AB = BC = CD = DA = c\)。
那么,
\(S_{\text {正方形}EFGH} = (b - a)^2\) ,
\(S_{\text {△}AEB} = S_{\text {△}BFC} = S_{\text {△}CGD} = S_{\text {△}DHA} = \frac {a \times b} {2}\) ,
\(4S_{\text {△}} = 2ab\),
\(∴S_{\text{正方形}ABCD} = 4S_{\text {△}} + S_{\text{正方形}EFGH} = (b - a)^2 + 2ab = a^2 - 2ab + b^2 + 2ab = a^2 + b^2\)
又\(\text{∵} S_{\text{正方形}ABCD} = c^2\)
\(\text{∴}a^2 + b^2 = c^2\)
证毕。
青朱出入图

没错就是这个,上面那张图多看几遍就会恍然大悟。
刘徽(约225年-约295年),山东淄博淄川人,三国时代魏国数学家,梁敬王刘定国之孙菑乡侯刘逢喜的后裔。
青朱出入图,是东汉末年数学家刘徽根据“割补术”运用数形关系证明勾股定理的几何证明法,其法富有东方智慧(?莫名想起这个),特色鲜明、通俗易懂。
利用相似三角形的证法
有许多勾股定理的证明方式,都是基于相似三角形中两边长的比例。
设 \({\displaystyle ABC}\) 为一直角三角形,直角于 \({\displaystyle \angle C}\)(看右图)。从点 \({\displaystyle C}\) 画上三角形的高,并将此高与 \({\displaystyle {\overline {AB}}}\) 的交叉点称之为 \({\displaystyle H}\)。此新 \({\displaystyle \bigtriangleup ACH}\) 和原本的 \({\displaystyle \bigtriangleup ABC}\) 相似,因为在两个三角形中都有一个直角(这又是由于“高”的定义),而两个三角形都有 \({\displaystyle A}\) 这个共同角,由此可知第三只角都是相等的。同样道理,\({\displaystyle \bigtriangleup CBH}\) 和 \({\displaystyle \bigtriangleup ABC}\) 也是相似的。这些相似关系衍生出以下的比率关系:
因为
\({\displaystyle {\overline {BC}}=a,{\overline {AC}}=b,{\mbox{ and }}{\overline {AB}}=c,\!}\)
所以
\({\displaystyle {\frac {a}{c}}={\frac {\overline {HB}}{a}}{\mbox{ and }}{\frac {b}{c}}={\frac {\overline {AH}}{b}}.\,}\)
可以写成
\({\displaystyle a^{2}=c\times {\overline {HB}}{\mbox{ and }}b^{2}=c\times {\overline {AH}}.\,}\)
综合这两个方程,我们得到
\({\displaystyle a^{2}+b^{2}=c\times {\overline {HB}}+c\times {\overline {AH}}=c\times ({\overline {HB}}+{\overline {AH}})=c^{2}.\,\!}\)
换句话说:
\({\displaystyle a^{2}+b^{2}=c^{2}.\,\!}a^2+b^2=c^2.\,\!\)
欧几里得的证法
在定理的证明中,我们需要如下四个辅助定理:
-
SAS(如果两个三角形有两组对应边和这两组边所夹的角相等,则两三角形全等。)
-
三角形面积是任一同底同高之平行四边形面积的一半。
-
任意一个正方形的面积等于其二边长的乘积。
-
任意一个矩形的面积等于其二边长的乘积。
其中3、4两个定理小学已经讲过了,这里不再赘述。
为了证明勾股定理,我们首先证明SAS。
由几何直观可得:如果两个三角形有两组对应边和这两组边所夹的角相等,则两三角形全等。
证毕。
好吧,SAS是一个公理(依据人类理性的不证自明的基本事实<来自百度百科>)。
下面是欧几里得对于勾股定理的证明。
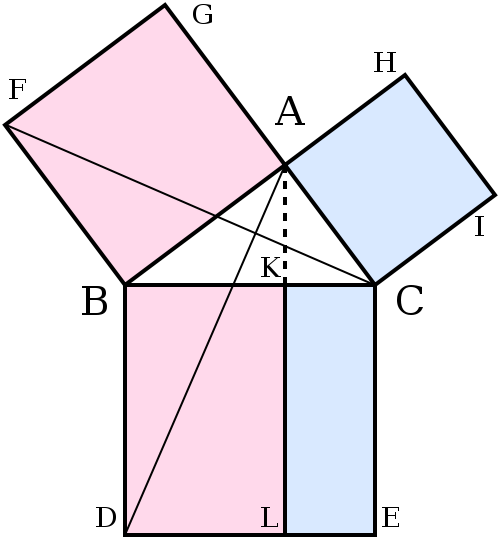
- 设 \({\displaystyle \triangle ABC}\) 为一直角三角形,其直角为 \({\displaystyle \angle CAB}\) 。
- 其边为 \({\displaystyle {\overline {BC}}}\)、\({\displaystyle {\overline {AB}}}\)、和 \({\displaystyle {\overline {CA}}}\),依序绘成四方形 \({\displaystyle CBDE}\)、\({\displaystyle BAGF}\) 和 \({\displaystyle ACIH}\)。
- 画出过点 \({\displaystyle A}\) 之 \({\displaystyle {\overline {BD}}}\)、\({\displaystyle {\overline {CE}}}\)的平行线。此线将分别与 \({\displaystyle {\overline {BC}}}\) 和 \({\displaystyle {\overline {DE}}}\) 直角相交于 \({\displaystyle K}\)、\({\displaystyle L}\)。
- 分别连接 \({\displaystyle {\overline {CF}}}\)、\({\displaystyle {\overline {AD}}}\),形成两个三角形 \({\displaystyle BCF}\)、\({\displaystyle BDA}\)。
- \({\displaystyle \angle CAB}\) 和 \({\displaystyle \angle BAG}\) 都是直角,因此 \({\displaystyle C}\)、\({\displaystyle A}\) 和 \({\displaystyle G}\)都是共线的,同理可证 \({\displaystyle B}\)、\({\displaystyle A}\) 和 \({\displaystyle H}\)共线。
- \({\displaystyle \angle CBD}\) 和 \({\displaystyle \angle FBA}\) 皆为直角,所以 \({\displaystyle \angle ABD}\) 相等于 \({\displaystyle \angle FBC}\)。
- 因为\({\displaystyle {\overline {AB}}}\) 和 \({\displaystyle {\overline {BD}}}\) 分别等于 \({\displaystyle {\overline {FB}}}\) 和 \({\displaystyle {\overline {BC}}}\),所以 \({\displaystyle \triangle ABD}\) 必须全等于 \({\displaystyle \triangle FBC}\)。
- 因为 \({\displaystyle A}\) 与 \({\displaystyle K}\) 和 \({\displaystyle L}\) 在同一直线上,所以四方形 \({\displaystyle BDLK}\) 必须二倍面积于 \({\displaystyle \triangle ABD}\)。
- 因为 \({\displaystyle C}\)、\({\displaystyle A}\) 和 \({\displaystyle G}\) 在同一直线上,所以正方形 \({\displaystyle BAGF}\) 必须二倍面积于 \({\displaystyle \triangle FBC}\)。
- 因此四边形 \({\displaystyle BDLK}\) 必须和 \({\displaystyle BAGF}\) 有相同的面积=\({\displaystyle {\overline {AB}}^{2}}\)。
- 同理可证,四边形 \({\displaystyle CKLE}\) 必须有相同的面积 \({\displaystyle ACIH={\overline {AC}}^{2}}\)。
- 把这两个结果相加,\({\displaystyle {\overline {AB}}^{2}+{\overline {AC}}^{2}={\overline {BD}}\times {\overline {BK}}+{\overline {KL}}\times {\overline {KC}}}\)
- 由于 \({\displaystyle {\overline {BD}}={\overline {KL}}}{\displaystyle {\overline {BD}}={\overline {KL}}},{\displaystyle {\overline {BD}}\times {\overline {BK}}+{\overline {KL}}\times {\overline {KC}}={\overline {BD}}\left({\overline {BK}}+{\overline {KC}}\right)={\overline {BD}}\times {\overline {BC}}}\)
- 由于 \({\displaystyle CBDE}\) 是个正方形,因此 \({\displaystyle {\overline {AB}}^{2}+{\overline {AC}}^{2}={\overline {BC}}^{2}}{\displaystyle {\overline {AB}}^{2}+{\overline {AC}}^{2}={\overline {BC}}^{2}}\)。
欧几里得(希腊语:Ευκλειδης,古希腊语:Εὐκλείδης,前325年-前265年),有时被称为亚历山大里亚的欧几里得,以便区别于墨伽拉的欧几里得。希腊化时代的数学家,被称为“几何学之父”。他活跃于托勒密一世时期的亚历山大里亚,也是亚历山太学派的成员。他在著作《几何原本》中提出五大公设,成为欧洲数学的基础。欧几里得也写过一些关于透视、圆锥曲线、球面几何学及数论的作品。欧几里得几何被广泛的认为是数学领域的经典之作。
图形重新排列证法
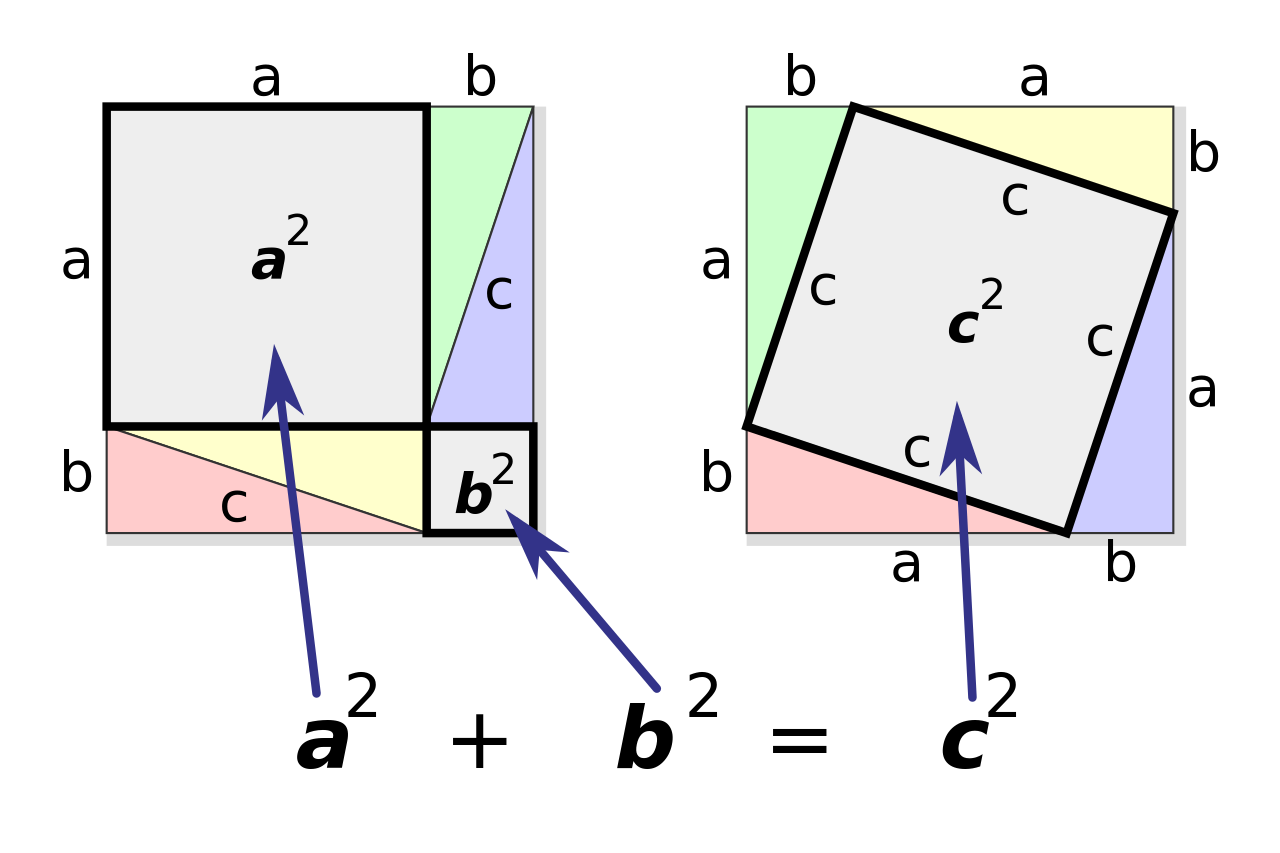
此证明以图形重新排列证明。两个大正方形的面积皆为 \({\displaystyle (a+b)^{2}}\)。把四个相等的三角形移除后,左方余下面积为 \({\displaystyle a^{2}+b^{2}}\),右方余下面积为 \({\displaystyle c^{2}}\),两者相等。证毕。
总统证法
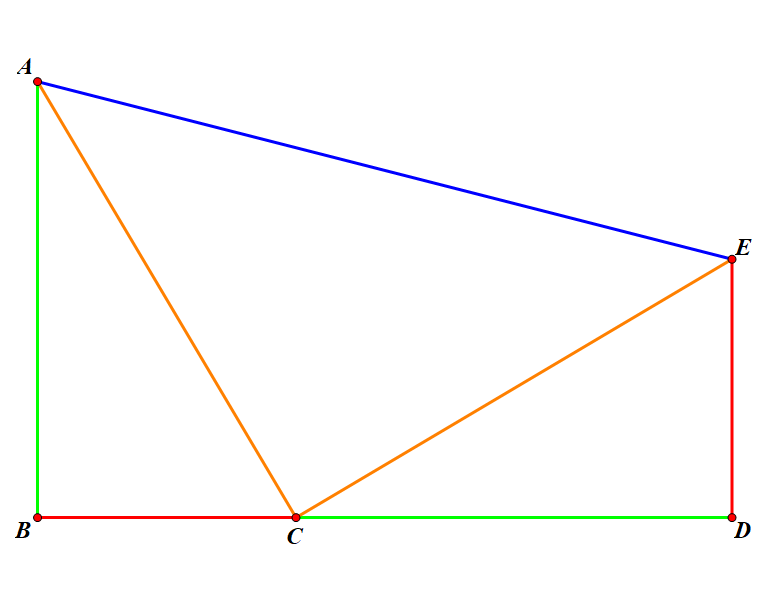
证明:\(\text{∵}S_{\text {梯形}ABCD} = \frac {1} {2} (a + b)^2 = \frac {1} {2} (a^2 + 2ab + b^2)\)
又\(\text{∵}S_{\text {梯形}ABCD} = S_{\text{△}AED} + S_{\text{△}EBC} + S_{\text{△}DEC} = \frac {1} {2}ab + \frac {1} {2}ba + \frac {1} {2}c = \frac {1} {2}(2ab + c^2)\)
\(\text {∴}c^2 = a^2 + b^2\)
证毕。
詹姆斯·艾伯拉姆·伽菲尔德(英语:James Abram Garfield,1831年11月19日—1881年9月19日),美国政治家、数学家,生于俄亥俄州。美国共和党人。南北战争期间加入北方军队,与南方奴隶制军队作战,拥有少将军衔。1880年加菲尔德当选为第20任总统,他是美国首位具有神职人员身份的总统。就职仅4个月即遭暗杀,是美国第二位被暗杀的总统。他在数学方面的贡献主要是在勾股定理的证明方面的新成就,他也是美国历史上唯一一位数学家出身的总统。他的第一夫人是卢克丽霞·鲁道夫,育有五子二女。
代码
相信你们看完了以上的证明已经对勾股定理有了初步的了解。那么,现在我们就可以开始写代码了:
#include <iostream>
using namespace std;
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (i * i + j * j == n * n) {
cout << i << ' ' << j << endl;
return 0;
}
}
这份已经是AC的代码了,如果让它运行得更快一点的话,可以稍稍地做一点优化。
为了让 \(a\),也就是 \(i\) 最小,\(a\) 肯定小于 \(b\)。所以可以让 \(j\) 从 \(i\) 开始循环。代码如下:
#include <iostream>
using namespace std;
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (i * i + j * j == n * n) {
cout << i << ' ' << j << endl;
return 0;
}
}
第一份代码运行了121ms,第二份运行了113ms。所以,我们要想办法优化自己的程序,使自己的程序加快不到10ms。
评价
此题涉及如此多的数学知识,建议至少评蓝。

