结对项目文档及结对编程感悟
王鹿鸣 13061100 邢浩 13061174
第一部分 结对编程感悟
在自己亲身经历了整个结对编程的过程,同时,也与不少其他的同学进行了交流后,我对于结对编程有了全新的一种理解。
结对编程本就是将复审发挥到极致的一种方式。通过两个人合作,一个人写、一个人“导航”,整个设计在写的过程中就得到了另一位同事的复审。毫无疑问,结对编程具有这样几个优势:
- 编码效率高
- 代码质量高
- 代码设计好
两个人一起写,互相督促,自然编码效率较高。同时,代码写出来后,立刻就由同事进行复审,质量当然和自己一个人写的不一样。遇到困难的时候也可以随时和伙伴商量,找出最合理的方案来。看上去,结对编程仿佛是万灵药,有百利而无一害。然而,经过了这一段时间的观察,我发现,这只是理想状态下的情况。很幸运,我们组正好属于一个非常理想的情况:好兄弟、技术水平相近、对待项目认真。所以,虽然一起弃疗了几天,但动手搞起项目来相当流畅,效率极高。但并非所有的组都如此幸运。有些组的两人相互间素不相识,有些组的两人间技术水平相差较多,沟通较为吃力,甚至有的同学表示根本找不到队友在哪里。因此,我认为结对编程其实远远不像看上去那般理想。毕竟是两个人一起合作写代码,倘若交流起来不流畅,反而会影响效率,不若一个人来的好。所以,结对编程对于参与双方的要求很高。必须是能够顺畅交流,比较对路的两个人,而非随意两个人均可。

我们的结对编程过程很顺利,我的队友的优势在于编码速度、算法能力,是个豪放而易于相处的人。他的劣势在于不太习惯写大段代码的时候有人在旁边看。而我长于架构设计、项目分析,性格比较平和。劣势在于工作效率相对低一些。结对编程的经历相当愉快。
第二部分 项目完整文档
(这一部分涵盖需求分析、接口设计、UML、算法设计等项目相关的内容,所以两人是一样的)
一、需求分析
根据此次的需求,我们将之前个人项目时的需求分析表进行了进一步完善,将此次新增的需求填入其中,结果如下。
|
|
功能 |
质量 |
约束 |
|
业务级需求 |
程序核心封装为Core库: 支持计算表达式结果 支持生成表达式 支持参数设定 |
发生错误时支持Exception |
|
|
用户级需求 |
自动生成四则运算,支持整数和真分数(以及负数) 支持括号 题目存入Exercises.txt中 同时生成题目答案,存入Answers.txt中 可以判断答案对错 支持一万道题目的生成 支持参数设定题目中: 题目数量 数据范围 最大运算符数量 (或运算过程中)有无分数 是否有乘除法 是否有括号 (或运算过程中)有无负数 |
用户输入有误时程序不崩溃 错误输入时需输出帮助信息 |
生成的算式需满足: 减法计算无负数 除法计算结果为真分数 运算符不超过3个 +和*交换不重复 真分数五分之三表示为3/5 真分数二又八分之三表示为2’3/8 Exercises.txt文件格式如下: 1. 四则运算题目1 2. 四则运算题目2 …… Answers.txt文件格式如下: 1. 答案1 2. 答案2 判卷结果输出到文件Grade.txt,格式如下: Correct: 5 (1, 3, 5, 7, 9) Wrong: 5 (2, 4, 6, 8, 10) |
|
开发级需求 |
写出至少10个测试用例确保你的程序能够正确处理各种情况。 需要有单元测试 |
算法复杂度在O(n)到O(nlogn)左右 经过Code Quality Analysis工具的分析并消除所有的警告 采用TFS进行管理 每个阶段完成后均需进行回归测试 单元测试覆盖率足够高 |
采用C++或者C#语言实现,可以使用.Net Framework 运行环境为32-bit Windows 7或8 分为五个阶段,每个阶段均需要一次提交: 计算及生成接口 “设置”功能接口 支持各类Exception 界面、测试、库的松耦合 改进程序并发布 |
二、接口设计
在接口的设计中,我们尽量保持信息隐藏、松耦合等原则。为了提升模块的内聚性,降低和外部的耦合性,我们只暴露出最必要的数据结构和接口函数。对于外界无需了解的任何信息,我们的接口中都不会将其暴露出去。以下是我们遵循这些想法设计的结果
(一)算式
算式采用以下的接口表达,通过标准的ToString进行输出。通过value()可以获得以分数形式表示的值,通过numValue则可以获得相应的double类型的值。
1 interface ExprAction 2 { 3 Fraction value(); 4 double numValue(); 5 }
由于外部不需要改变表达式本身,因此,我们只需要将该接口暴露给用户即可。至于该接口具体怎样实现,则是内部完成的。用户所需要的只是表达式的值以及输出该表达式而已,这已经足以满足用户所有的需求,因此,我们没有再暴露更多的东西给外部。
(二)计算及生成
public static ExprAction getExpr(String str)
通过字符串构造表达式。由于表达式支持返回答案的功能,故而这一接口可用于实现计算。
public static List<ExprAction> generate(int n, int r)
生成一定数量的表达式,参数n为题目数量,r为范围限制
上述两个接口也保持了我们之前的设计思路,完全通过ExprAction这个接口来将表达式的相关信息给用户,而不暴露任何多余的内容。这有利于我们维护内部的算法细节。例如,在实现的过程中,我们的生成算法几经调整,但除了对generate函数内部进行了一些改变之外,没有影响其余的任何部分。
(三)设置
设置通过settings函数进行,通过以下结构体将具体的配置信息传入到库中
1 public class Configure : ICloneable 2 { 3 // 最大运算符数目 4 public int MaxOperatorNum 5 { 6 get { return maxOperatorNum; } 7 set { maxOperatorNum = value; } 8 } 9 10 // 运算过程中能否有分数 11 public bool Fraction 12 { 13 get { return fraction; } 14 set { fraction = value; } 15 } 16 17 // 是否允许乘除法 18 public bool MulAndDiv 19 { 20 get { return mulAndDiv; } 21 set { mulAndDiv = value; } 22 } 23 24 // 是否允许括号 25 public bool Parentheses 26 { 27 get { return parentheses; } 28 set { parentheses = value; } 29 } 30 31 // 是否允许运算中出现负数 32 public bool Negative 33 { 34 get { return negative; } 35 set { negative = value; } 36 } 37 }
我们认为,采用单独的结构体传递数据相较于XML来说有这样几点优势。XML在传递设置的时候需要进行一定量的解析工作,而采用结构体是不需要的。在耦合性上,XML中的内容、设置等字段与我们的库也是紧密耦合的,所以,在我们看来XML就是一个以XML形式写成的结构体。我们最终还是会将XML解析成一个结构体的,与其这样,不如直接用结构体传递信息。
我们认为,即使最终的配置通过XML储存在磁盘上,那么解析XML的步骤也应当由前端来完成,而不应该由库本身来完成。库只负责接收设置并根据这一设置进行生成。而不应该牵扯到与用户相关的细节上。
这是我们最终设计库的接口时采用结构体的理由。
三、概要设计
(一)表达式文法
在对输入的字符串进行解析时,我们采用了文法制导的解析方式。这种方式实现较为简单,只需按照文法中的非终结符号进行自顶向下的递归分析即可构造出表达式所对应的语法树。因此,我们参考需求中给出的文法,将整个文法补齐。
1 <e> := <sf> | <e> + <e> | <e> − <e> | <e> × <e> | <e> ÷ <e> | (<e>) 2 <sf> := <f> | -<f> 3 <f> := <digit> | <digit>’<digit>/<digit> | <digit>/<digit> 4 <digit> := <n> | <n><digit2> 5 <n> := 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
然而,我们发现由于有+/-和*/÷两个优先级,直接采用上述文法无法有效地按照运算的优先级构造出正确的表达式树。乘除法和加减法是不同优先级的,构建表达式树时,先计算的应当放在下面,后计算的放在上面,通过上述文法进行语法分析,是难以达到这一要求的。
因此,我们改写了上述文法,以<e>来表示+/-这一优先级,<term>来表示*/÷这一优先级。这样就能够通过语法分析来构建出满足优先级关系的表达式树了。改写后的文法如下:
1 <e> := <e> + <term> | <e> − <term> | <term> 2 <term> := <term> × <factor> | <term> ÷ <factor> | <factor> 3 <factor> := <sf> | (<e>) 4 <sf> := <f> | -<f> 5 <f> := <digit> | <digit>’<digit>/<digit> | <digit>/<digit> 6 <digit> := <n> | <n><digit2> 7 <n> := 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
但该文法具有左递归性,无法直接进行自顶向下分析。所以为了使用自顶向下分析,我们又对该文法进行消除左递归的处理。消除左递归后的文法如下:
1 <e> := <term><e2> 2 <e2> := + <term> <e2> | − <term> <e2> | ε 3 <term> := <factor><term2> 4 <term2> := × <factor> <term2> | ÷ <factor> <term2> | ε 5 <factor> := <sf> | (<e>) 6 <sf> := <f> | -<f> 7 <f> := <digit> | <digit>’<digit>/<digit> | <digit>/<digit> 8 <digit> := <n> | <n><digit2> 9 <n> := 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
采用上述文法进行分析,即可构造出输入的表达式的表达式树。
(二)表达式树
我们将表达式的数据结构设计为一颗二叉树。每个叶节点为一个单独的数,每个内部节点为一个子表达式。整个表达式树按照中序遍历进行计算。在我们的设计中,我们将表达式树的内部节点和叶节点抽象为了ExprAction这个接口。
1 Fraction value(); 2 double numValue();
value()函数会将表达式的值以Fraction,即我们自定义的分数类的形式返回。而numValue则是其所对应的double值。numValue()主要用于单元测试。我们将按照分数的计算法则算出来的值,与我们直接使用浮点数计算出来的表达式的值进行比较,以确定我们的分数计算是否正确。
我们的Fraction类(叶节点)和Expression类(内部节点)这两个类实现了这一接口。
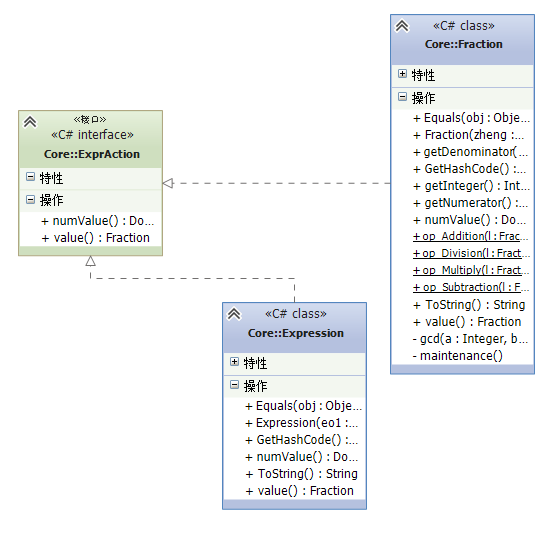
我们发现,四则运算的计算过程中的每一个步骤,实际上都是在根据左右两个表达式的值,计算当前表达式的值。因此整个计算过程只涉及Fraction直接的运算。因此,我们重载了Fraction类的四则运算操作符。
对于表达式树的设计,还有一点需要补充的是:Fraction和Expression是不可变对象。一旦被构造,则其对外表现出的状态是永远不变的。这样设计简化了代码实现的难度,也提升了程序的稳定性。
(三)表达式生成
首先我们提出一种不需要判重且可以生成全部不等价式的线性算法。
首先定义狭义上的一元的概念,一元就是指满足值域要求的自然数、真分数,然后狭义上的二元式就是指两个一元和一个操作符。
那么我们发现,在此基础上定义的三元式,四元式,多元式,他们的计算过程的最后一步必然是两个可以用一元表示的值按照最后剩下的操作符进行运算,也就是说,任何多元式都可归纳为二元式,而此时,一元就不仅仅是指狭义上的一元,而是包含了狭义上的二元式,多元式。
判断二元式的等价是非常简单的,只要使之+和*运算不满足交换律即可。
那么,我们只要由不等价的一元生成二元式,由一元和不等价的二元式生成三元式和四元式,那么这些式子一定都是不等价的。或者说,就是由广义上不等价的元生成所有广义上不等价的二元式。
给出其数学证明:
首先定义元a,元集A。二元式b,二元式集B。运算符f,运算符集F。
A := 满足值域要求的 自然数、真分数 | B; B := AFA; F := ‘+’|’-’|’*’|’/’;
如果b1=a1 f1 a2,b2=a3 f2 a4属于B,则:
b1与b2不等价的充分条件是:
f1 != f2 或
f1 == f2 且 f1 == ‘+’ 或 ‘*’ ,f1(a1,a3) != f2(a3,a4) && f1(a1,a3) != f2(a4,a3)
由以上定义和推理我们可以归纳出不生成重复表达式的线性算法,即用所有一元构造狭义二元式(即两个一元和一个运算符组成),之后用狭义二元式和一元构造足 够数目的广义二元式(即二元式本身也可作为元),只要在递归和迭代的生成过程中,任意二元式满足不重复的充分条件,则一定没有重复的二元式。
现在我们已经有了一个高效的线性生成算法,然而我们按照需求把它调整成随机化。
由上述算法不难看出,他是由少元向多元生成的,所以直接打乱顺序的方法是不行的。
所以我们采取这样的做法,首先生成所有的狭义一元,之后把这些一元打乱顺序,之后每次取极小一部分一元进行生成,并将生成结果存储,之后再取一小部分一元,先于其自身生成,之后再将其结果与上次生成的所有表达式组合进行生成,全部生产完之后将这些第二次生成的表达式合并到第一次的结果中,重复此操作直到满足个数或者全部生成完成为之。
最后由于我们采取的数据结构,直接这样输出还是有一定的线性规律,之后再把所有结果打乱一次顺序即可。
这种生成算法效率极高,30000个表达式的生成耗时1s左右。
四、单元测试
我们对代码进行了细致而详细的单元测试。单元测试对于我们代码的正确性有很大的帮助。由于TFS始终连接出错,因此,我们暂时采用了git进行版本控制。每次进行git pull拉取下来同伴的代码后,我们都会跑一遍所有的单元测试,以确保合并正确,并且本地新增的代码没有导致原有功能的倒退。
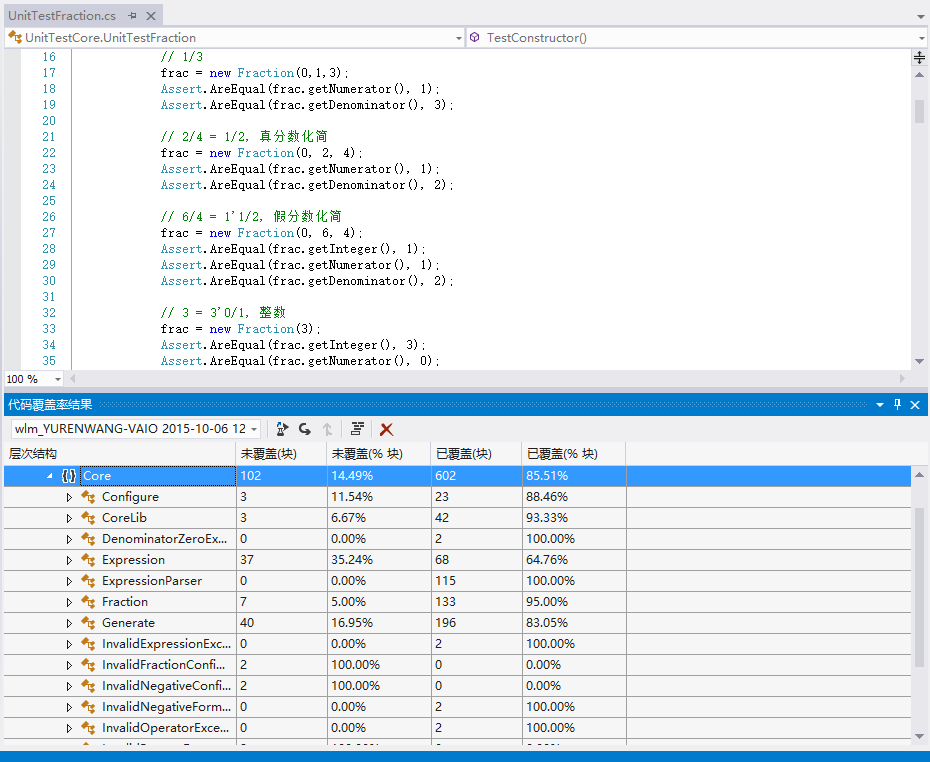
我们的代码整体的覆盖率比较高。对于一些比较重要的类,我们的覆盖率更是高达90%以上。多数没有被覆盖到的代码都是与随机生成相关的,由于其本身的随机性,难以达到单元测试的结果可以重现的要求。所以,这部分代码我们并没有进行单元测试。其余的相对较容易测试的代码,我们都进行了相应的单元测试。特别是解析表达式、带分数等关键的类,我们都尽可能地覆盖到了所有分支。

