软件工程实践2019第三次作业
大家好,我是渣渣(学)灰,水平不高,请多指教!
|psp表格 | | | |
| - | - | - | - | - |
| PSP2.1 | Personal Software Process Stages | 预估耗时 | 实际耗时(分钟)
| Planning | 计划 | 30 | 10 |
| Estimate |估计这个任务需要多少时间 | 1440 | 3785 |
| Development |开发 | 360 | 660 |
| Analysis | 需求分析 (包括学习新技术) | 720 | 660 |
| Design Spec| 生成设计文档 | 90 | 15 |
| Design Review| 设计复审 | 15 | 15 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 10 | 5 |
| Design | 具体设计 | 420 | 330 |
| Coding | 具体编码 | 540 | 780 |
| Code Review |代码复审 | 20 | 60 |
| Test | 测试(自我测试,修改代码,提交修改) | 30 | 20 |
| Reporting | 报告 | 30 | 20 |
| Test Repor | 测试报告 | 30 | 20 |
| Size Measurement | 计算工作量 | 5 | 5 |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 5 | 5 |
| 合计 | |2345 | 2650 |
说到数独的话,一般都是碰运气吧,但是考虑到33还可以暴力求解,99完全不可能,所以放弃暴力求解。
仔细想想,平常我们都是用直观法来求解数独的,具体来说就是,利用数独的每一行,每一列,每一宫都是1-n,n个数字恰好都只出现过一次。因此考虑每个数字出现的频率就可以了。但是这样先要统计各个字符出现的次数,然后再具体某一格,每次都要做至少n个判断,再考虑每一行,列,宫的所有格,还要平衡他们之间的关系反而变得复杂了。
而回溯法我又不是很懂,所以只能考虑排除法。
关于排除法的具体思想,大佬讲的比我清楚(图特别多系列):
莫多心情小站
[趁年华~]https://www.cnblogs.com/a1164520408/p/11559785.html
Martrix-revolution
另外,
baidu
独·数之道 | 数独爱好者
琳琅在线--数独游戏
数独- 入门级 #54874 -- 欧泊颗在线数独游戏
免费的在线数独
数独- 免费玩、打印并分享数独谜题
hoduku
最后这几个貌似是数独爱好者建起来的,里面介绍了目前已知的各种办法,可以说是相当多了。毫无疑问,如果是对于一百阶以上的数独来说,这些方法都是优化算法的来源。唯一美中不足的是,这个页面全都是英语,比做阅读理解还要累人。
我的算法完全是借鉴莫多的排除法的思想,

(当然我不可能去干抄代码这种事情,那样就鸭蛋了,还是臭鸭蛋了)我是按照自己的理解,重新再写了一遍,不过没有用递归,而是用循环替代,增加了一个计算循环次数的函数,算是一点小小的修改。所以程序跟他有同样问题,而且我的代码写的并不是很周全,我没有考虑到那种有歧义的情况,也没有和他一样消除那种可以消除歧义的情况。
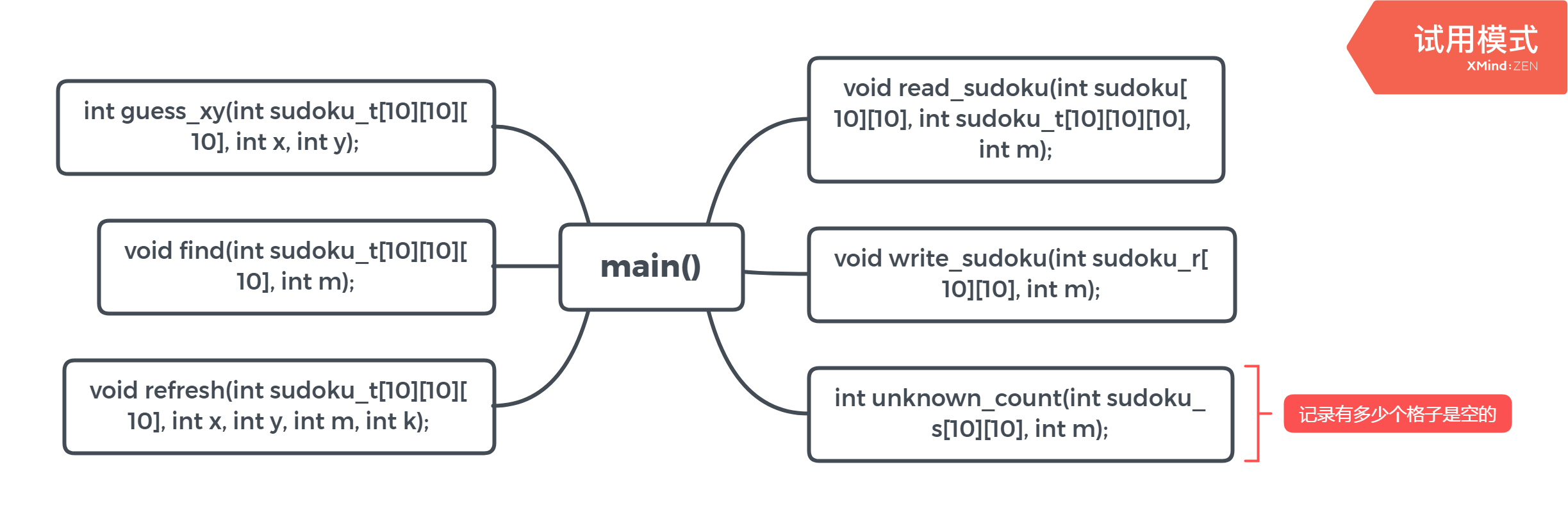
他是利用inside的函数和outside函数递归,我试着改成循环实现一样的效果。下面具体说说我的设计思路。
int sudoku[10][10] = { 0 }; //记录原始的数独数据,其中0为未知
int sudoku_s[10][10] = { 0 }; //记录原始的数独状态,1为已确定,0为未知
int sudoku_r[10][10] = { 0 }; //记录临时的数独数据,其中0为未知
int sudoku_t[10][10][10] = { 0 }; //每个单元填入数据的合法性记录,值为1表示不可以选择该数字填入
int m, n;
FILE *ip, *op;
void read_sudoku(int sudoku[10][10], int sudoku_t[10][10][10], int m);
int guess_xy(int sudoku_t[10][10][10], int x, int y);
void refresh(int sudoku_t[10][10][10], int x, int y, int m, int k);
int unknown_count(int sudoku_s[10][10], int m);
void find(int sudoku_t[10][10][10], int m);
void write_sudoku(int sudoku_r[10][10], int m);
Main函数是每次都读一个棋盘,然后处理一个棋盘,最后输出这个棋盘的答案。然后才读入下一个棋盘重复上述操作。
int main(int argc, char *argv[])
{
m = (int)argv[2]; //m 宫格阶级(3~9的整数)
n = (int)argv[4]; //n 待解答盘面数目
char *i = argv[6]; //刚开始忘了argv是*char,以为是FILE*
char *o = argv[8];
for (int s = 0; s < n; s++)
{
if ((ip = fopen(i, "r")) == NULL) {
printf("open file fail!\n");
exit(EXIT_SUCCESS);
}
read_sudoku(sudoku, sudoku_t, m);;
int g = unknown_count(sudoku_s, m);
for (int h = 1; h <= g; h++)
{
find(sudoku_t, m);
}
if ((ip = fopen(i, "w+")) == NULL) {
printf("open file fail!\n");
exit(EXIT_SUCCESS);
}
fclose(ip);
fclose(op);
}
return 0;
}
首先当然是unknow_count函数,因为如果棋盘上只有k处不知道该填什么数字的话,只要考虑这k处的情况就行,就不用试探这k处以外的地方是否需要填入数字。这看起来会有点绕口,但确实很有用。请务必充分理解这一点以后再看下面的内容。
int unknown_count(int sudoku_s[10][10],int m) { //统计未知的格子个数
int k = 0;
for (int i = 1; i <=m; i++)
{
for (int j = 1; j <= m; j++)
{
if (sudoku_s[i][j] == 0)
{
k++;
}
}
}
return k;
}
然后就是find函数,假设极其理想的条件下,如果棋盘有唯一解,那么它总是大概率在棋盘的某一处会出现这样的情况,就是这一个空格恰好只能填入某一个确定的数字而不允许填入其他的数字。于是我们就把这个数字填进去,然后修改相应的数据以及当前的状态。当然这里需要调用refresh函数一起完成当前的状态。
void find(int sudoku_t[10][10][10],int m) {
for (int x = 1; x <= m; x++)
{
for (int y = 1; y <= m; y++)
{
int k = guess_xy(sudoku_t, x, y);
if (k)
{
refresh(sudoku_t, x, y, m, k);
}
}
}
}
int guess_xy(int sudoku_t[10][10][10],int x,int y) { //若(x,y)对应的格子只有唯一一种可能则填入
int k = 0;
//for (int i = 1; i <= m; i++)
//{
for (int j = 1; j <= 9; j++)
{
k = k + sudoku_t[x][y][j];
}
//}
if ( k == 8 )
{
for (int i = 1; i <= 9; i++) {
if (sudoku_t[x][y][i] == 0)
{
sudoku_r[x][y] = i; //修改数据记录
sudoku_s[x][y] = 1; //修改已知记录,注意合法性记录还没改
return i;
}
}
}
else {
return 0;
}
}
void refresh(int sudoku_t[10][10][10], int x, int y,int m,int k) { //刷新合法性记录,注意k表示(x,y)处只能选k
for (int i = 1; i <= m ; i++)
{
if(i != y)sudoku_t[x][i][k] = 1;
if(i != x)sudoku_t[i][y][k] = 1;
if (m == 4) {
if ((x == 1 || x == 3) && (y == 1 || y == 3))
{
sudoku_t[x + 1][y][k] = sudoku_t[x][y + 1][k] = sudoku_t[x + 1][y + 1][k] = 1;
}
else if ((x == 1 || x == 3) && (y == 2 || y == 4))
{
sudoku_t[x + 1][y][k] = sudoku_t[x][y - 1][k] = sudoku_t[x + 1][y - 1][k] = 1;
}
else if ((x == 2 || x == 4) && (y == 1 || y == 3))
{
sudoku_t[x - 1][y + 1][k] = sudoku_t[x - 1][y][k] = sudoku_t[x][y + 1][k] = 1;
}
else if ((x == 1 || x == 3) && (y == 1 || y == 3))
{
sudoku_t[x - 1][y][k] = sudoku_t[x][y - 1][k] = sudoku_t[x - 1][y - 1][k] = 1;
}
}
if (m == 6)
{
if ((x == 1 || x == 4) && (y == 1 || y == 3 || y == 5 ))
{
sudoku_t[x + 1][y][k] = sudoku_t[x + 2][y][k] = sudoku_t[x][y + 1][k] = sudoku_t[x + 1][y + 1][k] = sudoku_t[x + 2][y + 1][k] = 1;
}
else if ((x == 2 || x == 5) && (y == 1 || y == 3 || y == 5))
{
sudoku_t[x - 1][y][k] = sudoku_t[x + 1][y][k] = sudoku_t[x - 1][y + 1][k] = sudoku_t[x][y + 1][k] = sudoku_t[x + 1][y + 1][k] = 1;
}
else if ((x == 3 || x == 6) && (y == 1 || y == 3 || y == 5))
{
sudoku_t[x - 2][y][k] = sudoku_t[x - 1][y][k] = sudoku_t[x - 2][y + 1][k] = sudoku_t[x - 1][y + 1][k] = sudoku_t[x][y + 1][k] = 1;
}
else if ((x == 1 || x == 4) && (y == 2 || y == 4 || y == 6))
{
sudoku_t[x + 1][y][k] = sudoku_t[x + 2][y][k] = sudoku_t[x][y - 1][k] = sudoku_t[x + 1][y - 1][k] = sudoku_t[x + 2][y - 1][k] = 1;
}
else if ((x == 2 || x == 5) && (y == 2 || y == 4 || y == 6))
{
sudoku_t[x - 1][y][k] = sudoku_t[x + 1][y][k] = sudoku_t[x - 1][y - 1][k] = sudoku_t[x][y - 1][k] = sudoku_t[x + 1][y - 1][k] = 1;
}
else if ((x == 3 || x == 6) && (y == 2 || y == 4 || y == 6))
{
sudoku_t[x - 2][y][k] = sudoku_t[x - 1][y][k] = sudoku_t[x - 2][y - 1][k] = sudoku_t[x - 1][y - 1][k] = sudoku_t[x][y - 1][k] = 1;
}
}
if (m == 8)
{
if ((x == 1 || x == 3 || x == 5 || x == 7) && (y == 1 || y == 5))
{
sudoku_t[x + 1][y][k] = sudoku_t[x][y + 1][k] = sudoku_t[x][y + 2][k] = sudoku_t[x][y + 3][k] = sudoku_t[x + 1][y + 1][k] = sudoku_t[x + 1][y + 2][k] = sudoku_t[x + 1][y + 3][k] = 1;
}
else if ((x == 1 || x == 3 || x == 5 || x == 7) && (y == 2 || y == 6))
{
sudoku_t[x + 1][y][k] = sudoku_t[x][y + 1][k] = sudoku_t[x][y + 2][k] = sudoku_t[x][y - 1][k] = sudoku_t[x + 1][y + 1][k] = sudoku_t[x + 1][y + 2][k] = sudoku_t[x + 1][y - 1][k] = 1;
}
else if ((x == 1 || x == 3 || x == 5 || x == 7) && (y == 3 || y == 7))
{
sudoku_t[x][y - 2][k] = sudoku_t[x][y - 1][k] = sudoku_t[x][y + 1][k] = sudoku_t[x + 1][y - 2][k] = sudoku_t[x + 1][y - 1][k] = sudoku_t[x + 1][y][k] = sudoku_t[x + 1][y + 1][k] = 1;
}
else if ((x == 1 || x == 3 || x == 5 || x == 7) && (y == 4 || y == 8))
{
sudoku_t[x][y - 3][k] = sudoku_t[x][y - 2][k] = sudoku_t[x][y - 1][k] = sudoku_t[x + 1][y - 3][k] = sudoku_t[x + 1][y - 2][k] = sudoku_t[x + 1][y - 1][k] = sudoku_t[x + 1][y][k] = 1;
}
else if ((x == 2 || x == 4 || x == 6 || x == 8) && (y == 1 || y == 5))
{
sudoku_t[x - 1][y][k] = sudoku_t[x][y + 1][k] = sudoku_t[x][y + 2][k] = sudoku_t[x][y + 3][k] = sudoku_t[x - 1][y + 1][k] = sudoku_t[x - 1][y + 2][k] = sudoku_t[x - 1][y + 3][k] = 1;
}
else if ((x == 2 || x == 4 || x == 6 || x == 8) && (y == 2 || y == 6))
{
sudoku_t[x - 1][y][k] = sudoku_t[x][y + 1][k] = sudoku_t[x][y + 2][k] = sudoku_t[x][y - 1][k] = sudoku_t[x - 1][y + 1][k] = sudoku_t[x - 1][y + 2][k] = sudoku_t[x - 1][y - 1][k] = 1;
}
else if ((x == 2 || x == 4 || x == 6 || x == 8) && (y == 3 || y == 7))
{
sudoku_t[x][y - 2][k] = sudoku_t[x][y - 1][k] = sudoku_t[x][y + 1][k] = sudoku_t[x - 1][y - 2][k] = sudoku_t[x - 1][y - 1][k] = sudoku_t[x - 1][y][k] = sudoku_t[x - 1][y + 1][k] = 1;
}
else if ((x == 2 || x == 4 || x == 6 || x == 8) && (y == 4 || y == 8))
{
sudoku_t[x][y - 3][k] = sudoku_t[x][y - 2][k] = sudoku_t[x][y - 1][k] = sudoku_t[x - 1][y - 3][k] = sudoku_t[x - 1][y - 2][k] = sudoku_t[x - 1][y - 1][k] = sudoku_t[x - 1][y][k] = 1;
}
}
if (m == 9)
{
int u = (int)floor((x-1) / 3) + 1;
int v = (int)floor((y-1) / 3) + 1;
sudoku_t[u - 1][v - 1][k] = sudoku_t[u - 1][v][k] = sudoku_t[u - 1][v + 1][k] = sudoku_t[u][v - 1][k] = sudoku_t[u][v + 1][k] = sudoku_t[u + 1][v - 1][k] = sudoku_t[u + 1][v][k] = sudoku_t[u + 1][v + 1][k] = 1;
}
}
}
但这一切都完成的时候,我们惊讶的发现,又回到了最初理想的条件下(此处假设题目足够理想)。此时又刚好在棋盘的某一处有且只有一个数字允许被填入这个空格。这完全是刚才那种情况的重复。于是我们可以照着刚才的操作,又重复一次,以此类推。
那么问题来了,在最理想的条件下,我们到底要重复多少次这样的操作才能填满棋盘?答案是k次,就是刚才unknown_count()计算出来的结果——有多少格子不知道我们就重复多少次。
这看起来感觉很好笑,但是——理论上来说——在最理想的情况下,能解开某些答案。
尴尬,匿……

