《机器学习》第二次作业——第四章学习记录和心得

第四章 线性判据与回归

4.1 线性判据基本概念

1. 生成模型
在 \({x_n}\) 中直接学习：\({p(x)}\)
以贝叶斯为例：生成模型 ——(估计)——> 观测似然概率 ——+先验概率——> 联合概率 ——积分——> 边缘概率密度函数 P(x) ——> 后验概率 \(P(C_i, x)\)
缺点：在高维空间会出现维度灾难问题。
2. 判别模型
在 \({x_n}\) 中直接学习后验概率 \({P(C_i, x)}\)
优点：快速直接，省去了耗时的观测似然概率估计。
3. 线性判据
f(x) 是线性函数，则 f(x) 是线性判据；

  • 可以用于两类/多类分类，相邻两类之间的决策边界是线性的。
  • 计算量少，适用于训练样本比较少的情况。
    数学表达：

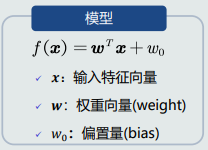
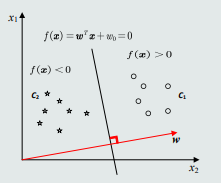
    决策边界：

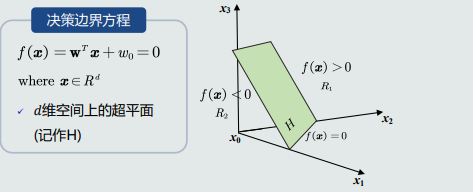
    决策边界H，设W垂直于决策边界上的任何向量，为H的法向量；（作用：决定决策边界H的方向）
    \(W_0\)的作用：
  • 决定了决策边界的偏移量，使其能够满足两个类输出值分被为正or负；
  • 决定决策边界相对于坐标原点的位置；
    样本到决策边界的距离：

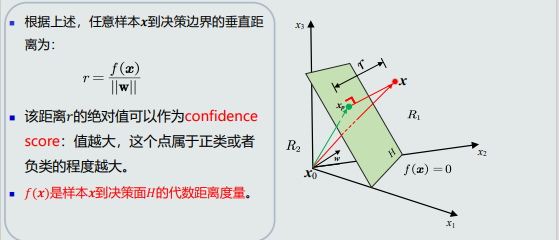
THEN How to learn the linear criterion?

4.2 线性判据学习概述

  1. 监督式学习(训练)过程
  2. 识别过程 \(f(x) < / > 0 ?\)
    key:寻找最优解？
  • 解不唯一；
  • 参数空间&解域（从解域中找到最优解）；
    • 设计目标函数 + 约束条件（提高泛化能力）
    • 最大/最小化目标函数

4.3 并行感知机算法

tips:(根据目标函数的不同，设计不同的线性判据算法)
目的：根据标记过的训练样本(监督式)，学习参数 \(W , W_0\)

预处理：在特征空间中增加一个维度，是的决策边界可以通过原点； 翻转C2类的样本，是的所有样本处于该平面的同一侧。
目标函数：被错误分类的样本最少(输出值 \(f(x)\)是负数)。
？？？如何最小化目标函数？

* 求偏导：不可行，因为偏导不含有a；
* 梯度下降法 get√

4.4 串行感知机算法

如果说并行感知机算法是一次全部给出，那么串行感知机算法就是一个一个串行给出。
思想：当前样本被错误分类的程度最小。
目标函数：

最小化目标函数：仍然使用梯度下降法来求解a;
算法：初始步长——>迭代更新(可能遍历多次)——>停止迭代(所有训练样本的输出值都大于0)。
收敛性：收敛性只是保证算法会停止，但是无法保证最终的结果是最优的。(全局最优和局部最优)——>(如果目标函数是\(J(a)\)是凸函数，那么局部最优就是全局最优)。
步长与收敛：步长决定收敛的速度。
？question:当样本处于决策边缘的时候，对该样本的决策有很大的不确定性。
solve：加入Margin约束，提高泛化能力。(不再以0为标准，以b为标准)
最小化目标函数：求关于参数向量a的偏导。

4.5 Fisher线性判据

把原空间各店x投影到新的一位空间 y.
\(y = w^T + w_0\)
原理：合适的投影轴(两个样本在该轴上的重叠尽可能少)
投影之后不同样本的类间差异尽可能大(均值之差)，类内样本离散程度尽可能小(协方差矩阵)。

存在问题：两类部分样本在决策边界附近犬牙交错。

4.6 支持向量机的基本概念

different：感知机：从最小化分类误差角度来设计；
Fisher线性判据：最大化类间距离，最小化类内散度。
支持向量机：训练样本的间隔(最近的训练样本到决策边界之间的间隔)要大一些。
间隔定义：\(d_+ && d_-\)
间隔计算：

支持向量机(SVM)：最大化总间隔。

4.7 拉格朗日乘数法

拉格朗日乘数法：用于解决支持向量机的目标函数的一个条件优化问题。
等式约束：f(x)的极值点\(x^*\)必须位于曲线g(x)=0上。
tips:往负梯度方向移动，与负梯度方向平行则停止。
不等式约束：

* 极值点落在可行区域内
   * 直接通过(梯度)f(x)=0来获得极值点；
* 极值点落在可行域边界

对偶可行性：始终存在 (lambuda>=0)，满足驻点条件。
KTT条件：最小化问题；多个约束问题。

4.8 拉格朗日对偶问题

？？question：拉格朗日带有约束条件，如何优化求解？主问题难以求解或者是NP难问题。

主问题最优值得下界：对偶函数。

对偶问题的凹凸性：逐点最小值函数min是凹函数——>对偶函数是凹函数——>对偶问题是凸优化。
(弱对偶性；强对偶性)

4.9 支持向量机学习算法

带不等式约束的优化问题使用拉格朗日对偶法求解。
key:构造对偶函数 。
对偶问题的求解：二次规划问题+参数最优化。
决策过程：𝒘 和 𝑤0 的学习过程实际上是从训练样本中选择一组支持向量，并将这些支持向量存储下来，用作线性分类器。

4.10 软间隔支持向量机

软间隔：克服过拟合。
(可以将SVM的硬间隔（hard margin）放宽到软间隔（soft margin），允许一些训练样本出现在间隔区域内，从而具备一定的克服过拟合的能力)
设计思想：引入松弛变量。
分类器表示：

构建目标函数——>构建拉格朗日函数——>构建对偶函数(在极值点的到对偶函数\(L_D\))

4.11 线性判据多类分类

多类分类的本质：非线性
需要：

  • 一个模型：能刻化非线性的决策边界。
  • 多个模型：多个模型（线性/非线性）组合成非线性决策边界。
  • 组合方式：并行组合、串行组合。

思路一：One-to-all
假设每个类与剩余类可分，总共需要训练K个分类器。
问题：每个分类器的正负类样本个数不均衡。
混淆区域问题：
* 拒绝选项
* 重叠。

思路二：线性机

  • 假设：假设每个类与剩余类线性可分。
  • 训练：基于one-to-all策略训练𝐾个线性分类器𝑓𝑖，每个分类器对应一个类𝐶𝑖。
  • 决策：使用输出值投票法（max函数）给定测试样本𝒙，其属于所有分类器中输出值最大的那个类。

取输出值最大：该值最大表示属于该类的可能性越大。
线性机 = 𝐾个线性模型 + 一个max函数
决策边界：

  • 通过max函数的引入，线性机将特征空间最终分为𝐾个决策区域。
  • 决策边界𝐻𝑖𝑗垂直于超平面(𝒘𝑖 − 𝒘𝑗)
    • 输出值投票法：使用两类权重𝒘向量的差值决定相邻两类之间的决策边界；
    • 标签识别法：利用每一类的权重𝒘向量决定该类与剩余类之间的决策边界。

优势：由于使用max函数，不再有混淆区域（即拒绝区域和重叠区域）。通过划定相邻两类之间的边界，分割了重叠区域和拒绝区域。
问题：可能出现最大的𝑓𝑖(𝒙) ≤ 0，即测试样本𝒙出现在拒绝区域。如果严格按照线性判据的定义，拒绝区域其实是线性机（基于one-to-all策略）无法正确判断的区域。
思路三：one-to-one策略
针对每两个类𝐶𝑖 和𝐶𝑗 ，训练一个线性分类器：𝑓𝑖𝑗 𝒙 = 𝒘𝑖𝑗𝑇𝒙 + 𝑤0𝑖𝑗。𝐶𝑖类真值为正；𝐶𝑗类真值为负。总共需要训练𝐾(𝐾 − 1) /2个分类器。

优势：适用于一些线性不可分的情况，从而实现非线性分类。
与one-to-all策略相比，不再有重叠区域。
问题：会出现拒绝选项。
总结：

  • 使用线性判据进行多类分类，本质上是利用多个线性模型组合而成一个非线性分类器。
  • 因此，决策边界不再是由单个超平面决定，而是由多个超平面组合共同切割特征空间。

4.12 线性回归

模型表达：

模型对比：

？？？线性回归模型如何学习？
待学习参数(给定学习样本学习参数w)——>给定N个训练样本——>目标函数(最小化均方误差)
目标函数的对比：

目标优化过程：

  • 展开目标函数；

  • 对参数w求偏导；
    目标优化：

  • 梯度下降法；

  • 最小二乘法；
    关于线性回归的概率解释：

    目标函数优化：

似然函数；
最大似然估计；
目标似然/MSE；(最大似然等同于最小化均方误差(MSE))

4.13 逻辑回归的概念


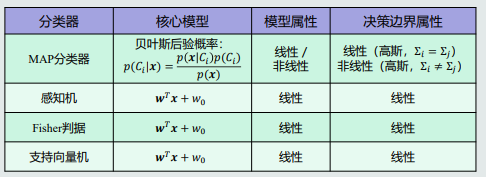
回顾：MAP分类器
如果两个类别数据分布的协方差矩阵不同（即Σ𝑖 ≠ Σ𝑗），则MAP分类器的决策边界是一个超二次型曲面，即非线性。
如果两个类别数据分布的协方差矩阵相同（即Σ𝑖 = Σ𝑗 ），则MAP分类器的决策边界是一个超平面，即线性。
Logit变换：
对于二类分类，MAP分类器通过比较后验概率的大小来决策。
Logit变换：𝐶1类的后验概率与𝐶2类的后验概率之间的对数比率。
在每类数据是高斯分布且协方差矩阵相同的情况下，由于Logit变换等同于线性判据的输出，所以在此情况下Logit(z) 是线性的。
Sigmoid函数：连接线性模型和后验概率的桥梁
线性模型𝑓(𝒙) + Sigmoid函数 = 后验概率
逻辑回归：线性模型𝑓(𝒙) + sigmoid函数。
决策边界：单个逻辑回归可以用于二类分类；给定两个类，逻辑回归的决策边界仍然是线性的超平面。

逻辑回归总结：

  • 逻辑回归本身是一个非线性模型。
  • 逻辑回归用于分类：仍然只能处理两个类别线性可分的情况。但是，sigmoid函数输出了后验概率，使得逻辑回归成为一个非线性模型。因此，逻辑回归比线性模型向前迈进了一步。
  • 逻辑回归用于拟合：可以拟合有限的非线性曲线。
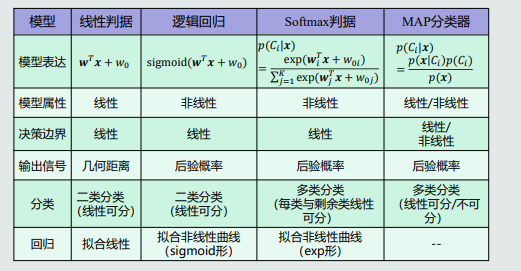
    模型对比：

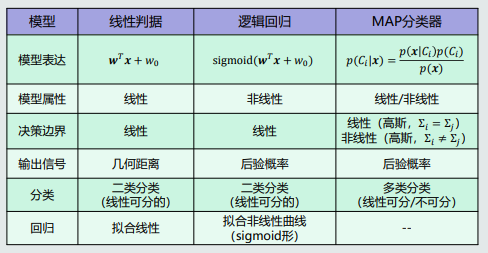
4.14 逻辑回归的学习

Key：给定训练样本，学习参数𝒘和𝑤0。
训练样本：

  • 正类（𝐶1类）样本的输出真值𝑡𝑛 = 1；

  • 负类（𝐶2类）样本的输出真值𝑡𝑛 = 0。

    • 注意：这种真值取值方式与SVM不一样。
      ？？如何设计目标函数呢？
      最大似然估计法(给定单个输入样本𝒙，模型输出的类别标签𝑙可以看做一个随机变量。)
      交叉熵解释：交叉熵可以用来度量两种分布的差异程度。
      给定𝑁个训练样本，把每个训练样本的交叉熵求和，得到最终的目标函数：

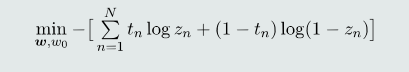
      目标函数优化：梯度下降法；
      步骤：

  • 对参数w求偏导；

  • 对参数w0求偏导；

  • 参数更新：采用梯度下降法更新w和w0;
    需要额外注意：梯度小时问题；
    key:迭代停止：如果迭代停止条件设为训练误差为0，或者所有训练样本都正确分类的时候才停止，则会出现过拟合问题。所以，在达到一定训练精度后，提前停止迭代，可以避免过拟合。

4.15 Softmax判据的概念

已知：逻辑回归输出：属于正类的后验概率
question：对于多类而言后验概率如何表达。
后验概率的多类情况：一个类与剩余类的后验概率比率。

  • 逻辑回归是由Logit变换反推出来的。

  • 由Logit变换可知：正负类后验概率比率的对数是一个线性函数。

  • 分类𝐾个类，可以构建𝐾个线性判据。第𝑖个线性判据表示𝐶𝑖类与剩余类的分类边界，剩余类用一个参考负类（reference class） 𝐶𝐾来表达。
    该后验概率的计算方法称为softmax函数；
    Softmax判据：𝐾个线性判据 + softmax函数。
    Softmax判据用于分类，等同于基于one-to-all策略的线性机。

    总结：

  • Softmax判据本身是一个非线性模型。

  • Softmax判据用于分类：只能处理多个类别、每个类别与剩余类线性可分的情况。但是， Softmax判据可以输出后验概率。因此，Softmax判据比基于one-to-all策略的线性机向前迈进了一步。

  • Softmax判据用于拟合：可以输出有限的非线性曲线。
    模型对比：

4.16 softmax判据的学习

4.17 核支持向量机

Kernel方法的基本思想：如果样本在原始特征空间（𝑋空间）线性不可分，可以将这些样本通过一个函数𝜑映射到一个高维的特征空间（Φ空间），使得在这个高维空间，这些样本拥有一个线性分类边界。
常见核函数：
多项式核函数：

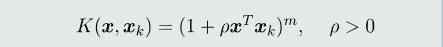
高斯核函数：

思维导图

机器学习第四章思维导图jpg文件

posted @ 2021-05-23 22:31  Star-T  阅读(171)  评论(0)  编辑  收藏  举报