hdu-2685 I won't tell you this is about number theory---gcd和快速幂的性质

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=2685

题目大意：

求gcd(am-1,an-1)%k

解题思路：

对于am-1 = (a - 1) * (1 + a + a2 + ... + am-1)

所以最开始的gcd就为a-1

对于两个1 + a + a2 + ... + am-1和1 + a + a2 + ... + an-1来说，可以找出gcd(m, n)那么久就可以提出gcd

比如：

1 + a + a2 + a3

1 + a + a2 + ... + a5

这两个可以写成（1+a）*（1 + a2） 和（1+a）*（1 + a2+ a4）

就提出公因式(1 + a)

这里公因式如何确定呢？

就是从0一直加到m和n的gcd-1次方，这样的话m和n才可以分解成多个从0---gcd-1的幂之和

所以，gcd(am-1,an-1) = （a-1）*（1 + a + a2 + a3 + ... + ag-1） = ag - 1

上式中g等于gcd(m, n)

也就是这个式子：

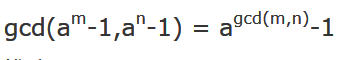
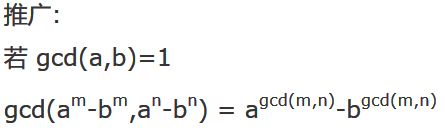
 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 typedef long long ll;
 4 int pow(int a, int b, int m)
 5 {
 6     int ans = 1;
 7     a %= m;
 8     while(b)
 9     {
10         if(b & 1)ans = ans * a % m;
11         a *= a;
12         a %= m;
13         b /= 2;
14     }
15     return ans;
16 }
17 int main()
18 {
19     int T, a, m, n, k, g;
20     cin >> T;
21     while(T--)
22     {
23         cin >> a >> m >> n >> k;
24         g = __gcd(m, n);
25         int ans = (pow(a, g, k) - 1) % k;
26         ans = (ans + k) % k;
27         cout<<ans<<endl;
28     }
29     return 0;
30 }

 

 

posted @ 2018-05-18 23:01  _努力努力再努力x  阅读(134)  评论(0)  编辑  收藏  举报