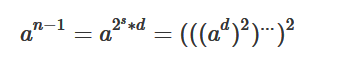大素数测试的Miller-Rabin算法

Miller-Rabin算法本质上是一种概率算法，存在误判的可能性，但是出错的概率非常小。出错的概率到底是多少，存在严格的理论推导。

一、费马小定理

假如p是质数，且gcd(a,p)=1，那么 a^(p-1)≡1（mod p）

如果存在a<p，且a^(p-1) % p != 1，则p肯定不是素数。

二、有限域上的平方根定理

三、Miller-Rabin算法

对于一个大数n，判断n是不是素数的时候，可以先考虑a^（n-1）≡ 1（mod n）

对于n-1，一定可以拆分成2^s+d：

可以从x = a^d开始，依次平方s次，每次平方的时候模上n，按照之前的平方根定理，如果模上n的结果为1的话，那么x一定是1，或者是n-1，如果不满足则不是素数，x=x²，再次循环。

每次随机选一个在2-n-1的数字作为a，可以重复测试。

由于mod上的是n，n是一个大数，所以快速幂中的乘法，需要用快速加法来实现。不然就算模上之后再相乘也会溢出。

 

 

#include<iostream>
#include<ctime>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = 1000000+10;
ll mul(ll a, ll b, ll m)
//求a*b%m
{
    ll ans = 0;
    a %= m;
    while(b)
    {
        if(b & 1)ans = (ans + a) % m;
        b /= 2;
        a = (a + a) % m;
    }
    return ans;
}
ll pow(ll a, ll b, ll m)
//a^b % m
{
    ll ans = 1;
    a %= m;
    while(b)
    {
        if(b & 1)ans = mul(a, ans, m);
        b /= 2;
        a = mul(a, a, m);
    }
    ans %= m;
    return ans;
}
bool Miller_Rabin(ll n, int repeat)//n是测试的大数，repeat是测试重复次数
{
    if(n == 2 || n == 3)return true;//特判
    if(n % 2 == 0 || n == 1)return false;//偶数和1

    //将n-1分解成2^s*d
    ll d = n - 1;
    int s = 0;
    while(!(d & 1)) ++s, d >>= 1;
    srand((unsigned)time(NULL));
    for(int i = 0; i < repeat; i++)//重复repeat次
    {
        ll a = rand() % (n - 3) + 2;//取一个随机数,[2,n-1)
        ll x = pow(a, d, n);
        ll y = 0;
        for(int j = 0; j < s; j++)
        {
            y = mul(x, x, n);
            if(y == 1 && x != 1 && x != (n - 1))return false;
            x = y;
        }
        if(y != 1)return false;//费马小定理
    }
    return true;
}
int main()
{
    int T;
    cin >> T;
    ll n;
    while(T--)
    {
        cin >> n;
        if(Miller_Rabin(n, 50))cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
}