hdu-2620 Ice Rain---数论（取模运算规律）

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=2620

题目大意：

给出n和k求：

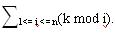
解题思路：

kmodi=k-i*[k/i] ，所以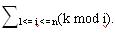=nk-（1*[k/1]+2*[k/2]+...+n*[k/n]）

只需求（1*[k/1]+2*[k/2]+...+n*[k/n]）

对于前sqrt(k)项，可以直接求解

对于后面的，可以枚举[k/i]取整得到的值来计算有多少个这样的值。

这样时间复杂度只有根号k

 

比如k = n = 25，需要求解（1*[k/1]+2*[k/2]+...+n*[k/n]）

对于前5项，直接求解

6到25项的结果分别是：

i	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
[k/i]	4	3	3	2	2	2	2	1	1	1	1	1	1	1	1	1	1	1	1	1

从6开始

[k/i] = 4 左区间：6　　右区间为25 / 4 = 6

[k/i] = 3 左区间：7　　右区间为25 / 3 = 8

[k/i] = 2 左区间：9　　右区间为25 / 2 = 12

[k/i] = 1 左区间：13　  右区间为25 / 1 = 25

可写出伪代码：

　　i从sqrt(k)+1到k

　　　　左区间 l = i；

　　　　取整的值x为 k / l

　　　　右区间为 r = k / x

　　　　右区间取n和右区间的较小值

　　　　取整的值x的个数：num = (r - l + 1) * (r + l) / 2　　　　这是由于求的是（1*[k/1]+2*[k/2]+...+n*[k/n]）前面还有系数需要相加

　　　　tot += num * x

　　　　i = r + 1

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
    ll n, k;
    while(cin >> n >> k)
    {
        ll a = n * k;
        if(n > k)n = k;
        ll m = sqrt(k + 0.5);
        ll tot = 0;
        if(n > m)
        {
            for(ll i = 1; i <= m; i++)
                tot += k / i * i;
            for(ll i = m + 1; i <= n; )//i就是左区间
            {
                ll x = k / i;
                ll r = k / x;           //r是右区间
                if(r > n)r = n;
                tot += (r + i) * (r - i + 1) / 2 * x;
                i = r + 1;
            }
        }
        else
        {
            for(ll i = 1; i <= n; i++)
                tot += k / i * i;
        }
        ll ans = a - tot;
        cout<<ans<<endl;
    }
    return 0;
}