hdu-2683 TCE-frep number system---完全数+二项展开式

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=2683

题目大意：

g（n）是n的因子和

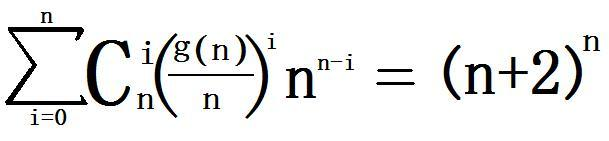
两种操作：

A a b 查询a b区间有多少个n满足上式。

Q a 查询a满不满足上式

解题思路：

上述右边二项式展开，就得到：

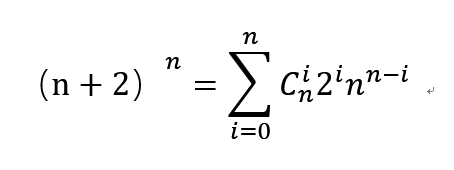
和上式对照，发现g(n) = 2n，由于g(n)是n的因子和，所以可以小于n的因子和就等于n

这就是完全数

而在2^63-1范围内只有8个完全数，直接打表即可

坑：给的区间不是标准的左端点 右端点形式给的，也就是A a b中a可能大于b，需要判断

 

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
typedef long long ll;
ll a[] ={6LL,28LL,496LL,8128LL,33550336LL,8589869056LL,137438691328LL,2305843008139952128LL};
int main()
{
    char s[10];
    while(cin >> s)
    {
        if(s[0] == 'A')
        {
            ll x, y;
            cin >> x >> y;
            if(x > y)swap(x, y);//坑在这里
            ll ans = 0;
            for(int i = 0; i < 8; i++)
                if(a[i] >= x && a[i] <= y)ans++;
            cout<<ans<<endl;
        }
        else if(s[0] == 'Q')
        {
            ll x;
            cin >> x;
            ll flag = 0;
            for(int i = 0; i < 8; i++)
                if(a[i] == x)flag = 1;
            cout<<flag<<endl;
        }
    }
    return 0;
}