hdu1852 Beijing 2008

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=1852

题目大意：

求2008^n的所有因子和m对k取余，然后求2008^m对k取余。

解题思路：

首先将2008因式分解，2008 = 2^3 * 251

所以2008^n = 2^(3n) * 251^(n)

因子和m =（2^(3n+1）- 1) * （251^(n+1) - 1）/ 250

m需要对k取余数。由于余数k和250可能不互质，也就是没有逆元存在，那么需要用到通用公式：

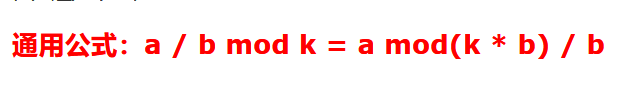
所以可以用快速幂求出（2^(3n+1）- 1) mod k

再求出（251^(n+1) - 1）mod (250 * k) / 250

两者相乘再对k求余数作为2008的指数

最后快速幂求出答案

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll pow(ll a, ll b, ll m)
{
    ll ans = 1;
    a %= m;
    while(b)
    {
        if(b & 1)ans = ans * a % m;
        b /= 2;
        a *= a;
        a %= m;
    }
    return ans;
}
int main()
{
    ll n, k;
    while(cin >> n >> k && n)
    {
        ll a = pow(2, 3 * n + 1, k) - 1;
        ll b = (pow(251, n + 1, 250 * k) - 1) % (250 * k);
        b /= 250;
        cout<<pow(2008, (a * b) % k, k)<<endl;//此处必须a*b需要先对k取余数，题目求的是因子和m对k取余数作为指数的值
    }
    return 0;
}