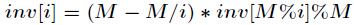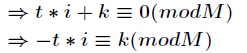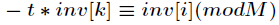逆元的求法
乘法逆元
对于缩系中的元素,每个数a均有唯一的与之对应的乘法逆元x,使得ax≡1(mod n)
一个数有逆元的充分必要条件是gcd(a,n)=1,此时逆元唯一存在
逆元的含义:模n意义下,1个数a如果有逆元x,那么除以a相当于乘以x。
下面给出求逆元的几种方法:
1.扩展欧几里得
给定模数m,求a的逆相当于求解ax=1(mod m)
这个方程可以转化为ax-my=1
然后套用求二元一次方程的方法,用扩展欧几里得算法求得一组x0,y0和gcd
检查gcd是否为1
gcd不为1则说明逆元不存在
若为1,则调整x0到0~m-1的范围中即可
1 ll extgcd(ll a, ll b, ll& x, ll& y) 2 //求解ax+by=gcd(a, b) 3 //返回值为gcd(a, b) 4 { 5 ll d = a; 6 if(b) 7 { 8 d = extgcd(b, a % b, y, x); 9 y -= (a / b) * x; 10 } 11 else x = 1, y = 0; 12 return d; 13 } 14 ll mod_inverse(ll a, ll m) 15 //求解a关于模上m的逆元 16 //返回-1表示逆元不存在 17 { 18 ll x, y; 19 ll d = extgcd(a, m, x, y); 20 return d == 1 ? (m + x % m) % m : -1; 21 }
2.费马小定理
在模为素数p的情况下,有费马小定理
a^(p-1)=1(mod p)
那么a^(p-2)=a^-1(mod p)
也就是说a的逆元为a^(p-2)
而在模不为素数p的情况下,有欧拉定理
a^phi(m)=1(mod m) (a⊥m)
同理a^-1=a^(phi(m)-1)
因此逆元x便可以套用快速幂求得了x=a^(phi(m)-1)
但是似乎还有个问题?如何判断a是否有逆元呢?
检验逆元的性质,看求出的幂值x与a相乘是否为1即可
PS:这种算法复杂度为O(log2N)在几次测试中,常数似乎较上种方法大
当p比较大的时候需要用快速幂求解
1 ll pow(ll a, ll b, ll m) 2 { 3 ll ans = 1; 4 a %= m; 5 while(b) 6 { 7 if(b & 1)ans = (ans % m) * (a % m) % m; 8 b /= 2; 9 a = (a % m) * (a % m) % m; 10 } 11 ans %= m; 12 return ans; 13 } 14 ll mod_inverse(ll a, ll m)//m是素数,a的逆元就是a的m-2次方 15 { 16 return pow(a, m - 2, m); 17 }
3、逆元不存在,求解a/b mod k(前提:b | a)
逆元存在时,a / b mod k 等价于a * B mod k(B是b模上k的逆元)
但是逆元不存在时
通用公式:a / b mod k = a mod(k * b) / b
证明:

之前的费马小定理和扩展欧几里得算法求逆元是有局限性的,它们都会要求a和m互素(此处的a和m是之前ax = 1(mod m)中的a和m,在这里应该是这里的b和m互素),如果不互素逆元不存在。b*m很大的时候不适合该公式
逆元打表
有时会遇到这样一种问题,在模质数p下,求1~n逆元 n< p(这里
它的推导过程如下,设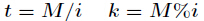
对上式两边同时除
再把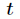
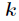
初始化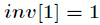

另外有个结论


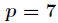
1 void Init_inv(int n, int p)//p为素数 2 { 3 inv[1] = 1; 4 for(int i = 2; i <= n; i++) 5 inv[i] = (ll)(p - p / i) * inv[p % i] % p; 6 }
https://blog.csdn.net/guhaiteng/article/details/52123385