数论专题(三)数论常用算法
转载自:https://blog.csdn.net/whereisherofrom/article/details/78922798
三、数论常用算法
1、Rabin-Miller
大素数判定
2、Pollard-rho 大数因式分解
3、RSA原理
三、数论常用算法
1、Rabin-Miller 大素数判定
对于一个很大的数n(例如十进制表示有100位),如果还是采用试除法进行判定,时间复杂度必定难以承受,目前比较稳定的大素数判定法是拉宾-米勒(Rabin-Miller)素数判定。
拉宾-米勒判定是基于费马小定理的,即如果一个数p为素数的条件是对于所有和p互素的正整数a满足以下等式: 。
。
然而我们不可能试遍所有和p互素的正整数,这样的话和试除比算法的复杂度反而更高,事实上我们只需要取比p小的几个素数进行测试就行了。
具体判断n是否为素数的算法如下:
i) 如果n==2,返回true;如果 n<2|| !(n&1), 返回false;否则跳到ii)。
ii) 令n = m*(2^k) + 1,其中m为奇数,则n-1 = m*(2^k)。
iii) 枚举小于n的素数p(至多枚举10个),对每个素数执行费马测试,费马测试如下:计算pre = p^m % n,如果pre等于1,则该测试失效,继续回到iii)测试下一个素数;否则进行k次计算next = pre^2 % n,如果next == 1 && pre != 1 && pre != n-1则n必定是合数,直接返回;k次计算结束判断pre的值,如果不等于1,必定是合数。
iv) 10次判定完毕,如果n都没有检测出是合数,那么n为素数。
伪代码如下:
bool Rabin_Miller(LL n) {
LL k = 0, m = n-1;
if(n == 2) return true;
if(n < 2 || !(n & 1)) return false;
// 将n-1表示成m*2^k
while( !(m & 1) ) k++, m >>= 1;
for(int i = 0; i < 10; i++) {
if(p[i] == n)
return true;
if( isRealComposite(p[i], n, m, k) ) {
return false;
}
}
return true;
}
LL k = 0, m = n-1;
if(n == 2) return true;
if(n < 2 || !(n & 1)) return false;
// 将n-1表示成m*2^k
while( !(m & 1) ) k++, m >>= 1;
for(int i = 0; i < 10; i++) {
if(p[i] == n)
return true;
if( isRealComposite(p[i], n, m, k) ) {
return false;
}
}
return true;
}
这里的函数isRealComposite(p, n, m, k)就是费马测试,p^(m*2^k) % n不等于1则n必定为合数,这是根据费马小定理得出的(注意)。n-1 = m*(2^k)
isRealComposite实现如下:
bool isRealComposite(LL p, LL n, LL m, LL k) {
LL pre = Power_Mod(p, m, n);
if(pre == 1) {
return false;
}
while(k--) {
LL next = Product_Mod(pre, pre, n);
if(next == 1 && pre != 1 && pre != n-1)
return true;
pre = next;
}
return ( pre != 1 );
}
LL pre = Power_Mod(p, m, n);
if(pre == 1) {
return false;
}
while(k--) {
LL next = Product_Mod(pre, pre, n);
if(next == 1 && pre != 1 && pre != n-1)
return true;
pre = next;
}
return ( pre != 1 );
}
这里Power_Mod(a, b, n)即a^b%n,Product_Mod(a, b, n)即a*b%n,而k次测试的基于费马小定理的一个推论:x^2 % n = 1当n为素数时x的解只有两个,即1和n-1。
2、Pollard-rho 大数因式分解
有了大数判素,就会伴随着大数的因式分解,Pollard-rho是一个大数分解的随机算法,能够在O(n ^(1/4) )的时间内找到n的一个素因子p,然后再递归计算n' = n/p,直到n为素数为止,通过这样的方法将n进行素因子分解。
Pollard-rho的策略为:从[2, n)中随机选取k个数x1、x2、x3、...、xk,求任意两个数xi、xj的差和n的最大公约数,即d = gcd(xi - xj, n),如果1 < d < n,则d为n的一个因子,直接返回d即可。
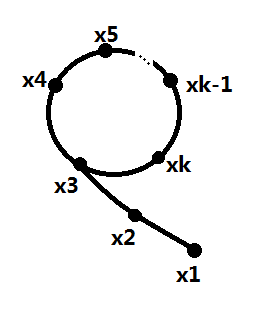
然后来看如何选取这k个数,我们采用生成函数法,令x1 = rand()%(n-1) + 1,xi = (xi-1 ^ 2 + 1 ) mod n,很明显,这个序列是有循环节的,就像图三-2-1那样。

图三-2-1
我们需要做的就是在它进入循环的时候及时跳出循环,因为x1是随机选的,x1选的不好可能使得这个算法永远都找不到n的一个范围在(1, n)的因子,这里采用歩进法,保证在进入环的时候直接跳出循环,具体算法伪代码如下:
LL Pollard_rho(LL n) {
LL x = rand() % (n - 1) + 1;
LL y = x;
LL i = 1, k = 2;
do {
i++;
LL p = gcd(n + y - x, n); // 这里传入的gcd需要是正数
if(1 < p && p < n) {
return p;
}
if(i == k) {
k <<= 1;
y = x;
}
x = Func(x, n);
}while(x != y);
return n;
}
LL x = rand() % (n - 1) + 1;
LL y = x;
LL i = 1, k = 2;
do {
i++;
LL p = gcd(n + y - x, n); // 这里传入的gcd需要是正数
if(1 < p && p < n) {
return p;
}
if(i == k) {
k <<= 1;
y = x;
}
x = Func(x, n);
}while(x != y);
return n;
}
3、RSA原理
RSA算法有三个参数,n、pub、pri,其中n等于两个大素数p和q的乘积(n = p*q),pub可以任意取,但是要求与(p-1)*(q-1)互素,pub*pri % () = 1 (可以理解为pri是pub的逆元),那么这里的(n, pub)称为公钥,(n, pri)称为私钥。(p-1)*(q-1)
RSA算法的加密和解密是一致的,令x为明文,y为密文,则:
加密:y = x ^ pub % n (利用公钥加密,y = encode(x) )
解密:x = y ^ pri % n (利用私钥解密,x = decode(y) )
那么我们来看看这个算法是如何运作的。
假设你得到了一个密文y,并且手上只有公钥,如何得到明文x,从decode的情况来看,只要知道私钥貌似就可以了,而私钥的获取方式只有一个,就是求公钥对(p-1)*(q-1)的逆元,如果(p-1)*(q-1)已知,那么可以利用扩展欧几里德定理进行求解,问题是(p-1)*(q-1)是未知的,但是我们有n = p*q,于是问题归根结底其实是难在了对n进行素因子分解上了,Pollard-rho的分解算法时间 复杂度只能达到O(n ^(1/4)
),对int64范围内的整数可以在几十毫秒内出解,而当n是几百位的大数的时候计算时间就只能用天来衡量了。
越努力,越幸运





