点(x1, y1)关于点(x0, y0)逆时针旋转a度后的坐标求解

问题描述：

求点(x1, y1)关于点(x0, y0)逆时针旋转a度后的坐标

 

思路：

1、首先可以将问题简化，先算点(x1, y1)关于源点逆时针旋转a度后的坐标，求出之后加上x0，y0即可。

 

2、关于源点旋转，用极坐标表示

设x1 = Rcos(θ), y1 = Rsin(θ)，绕源点逆时针旋转β度后得到坐标(x2, y2)等于(Rcos(θ + β) , Rsin(θ + β))

 

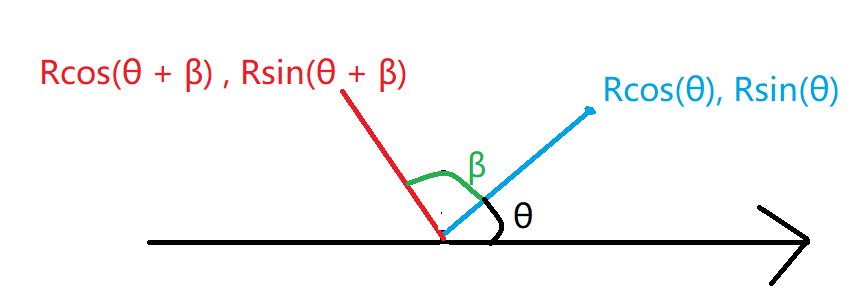
3、展开(Rcos(θ + β) , Rsin(θ + β))

变成 x2 = Rcos(θ)cos(β) - Rsin(θ)sin(β) 　　y2 = Rsin(θ)cos(β) + Rcos(θ)sin(β)

结合上面的x1 = Rcos(θ), y1 = Rsin(θ)

得到：x2 = x1cos(β) - y1sin(β)   　　y2 = x1sin(β) + y1cos(β)

 

4、转化成一般形式

x2 = (x1 - x0)cos(β) - (y1 - y0)sin(β) + x0   　　

y2 = (x1 - x0)sin(β) + (y1 - y0)cos(β) + y0