POJ-3321 Apple Tree---树状数组+DFS序

题目链接：

https://vjudge.net/problem/POJ-3321

题目大意：

题目大意级是说，给你一颗树，最初每个节点上都有一个苹果，有两种操作：修改（即修改某一个节点，修改时这一个节点苹果从有到无，或从无到有）和查询（查询某一个节点他的子树上有多少个苹果）。

解题思路：

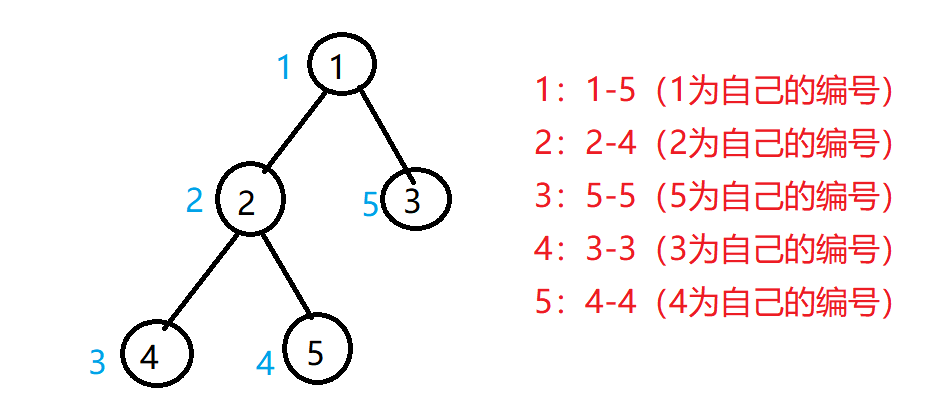
对树的每个节点进行编号，按照先序遍历进行编号，这样可以处理出一段区间，使得区间内都是点i的子树，求和的时候只要求区间和即可。

黑色是原来的编号，蓝色为用先序遍历得到的编号

超级坑的一点：

这里用vector<int>G[maxn]会超时

用vector<vector<int> > G(maxn)就过了

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<iostream>
  4 #include<algorithm>
  5 #include<string>
  6 #include<cmath>
  7 #include<set>
  8 #include<queue>
  9 #include<map>
 10 #include<stack>
 11 #include<vector>
 12 #include<list>
 13 #include<deque>
 14 #include<sstream>
 15 #include<cctype>
 16 #define REP(i, n) for(int i = 0; i < (n); i++)
 17 #define FOR(i, s, t) for(int i = (s); i < (t); i++)
 18 #define MEM(a, x) memset(a, x, sizeof(a));
 19 using namespace std;
 20 typedef long long ll;
 21 typedef unsigned long long ull;
 22 const int maxn = 1e5 + 10;
 23 const double eps = 1e-10;
 24 const int INF = 1 << 30;
 25 const int dir[4][2] = {1,0,0,1,0,-1,-1,0};
 26 const double pi = 3.1415926535898;
 27 int T, n, m, cases, tot;
 28 int tree[maxn], lef[maxn], rig[maxn], s[maxn];///s数组记录该节点是否有树
 29 vector<vector<int> >a(maxn);
 30 void dfs(int x)
 31 ///dfs给树节点编号，分别编成左节点和右节点，
 32 ///左节点就是本身，右节点是可到达的节点的最大编号，
 33 ///之后查询节点x的子树就可以直接查询[le[x], rig[x]]的区间和
 34 {
 35     lef[x] = tot;
 36     for(int i = 0; i < a[x].size(); i++)
 37     {
 38         tot++;
 39         dfs(a[x][i]);
 40     }
 41     rig[x] = tot;
 42 }
 43 int lowbit(int x)
 44 {
 45     return x&(-x);
 46 }
 47 int sum(int x)
 48 {
 49     int ret = 0;
 50     while(x > 0)
 51     {
 52         ret += tree[x];
 53         x -= lowbit(x);
 54     }
 55     return ret;
 56 }
 57 int add(int x, int d)
 58 {
 59     while(x <= n)
 60     {
 61         tree[x] += d;
 62         x += lowbit(x);
 63     }
 64 }
 65 int main()
 66 {
 67     int x, y;
 68     char c[5];
 69     while(scanf("%d", &n) != EOF)
 70     {
 71         MEM(lef, 0);
 72         MEM(rig, 0);
 73         MEM(s, 0);
 74         MEM(tree, 0);
 75         for(int i = 0; i < maxn; i++)a[i].clear();
 76         for(int i = 1; i < n; i++)
 77         {
 78             scanf("%d%d", &x, &y);
 79             a[x].push_back(y);
 80         }
 81         tot = 1;
 82         dfs(1);
 83         for(int i = 1; i <= n; i++)
 84         {
 85             s[i] = 1;
 86             add(i, 1);
 87         }
 88         scanf("%d", &m);
 89         while(m--)
 90         {
 91             scanf("%s%d", c, &x);
 92             if(c[0] == 'Q')
 93             {
 94                 cout << sum(rig[x]) - sum(lef[x] - 1) << endl;
 95             }
 96             else if(c[0] == 'C')
 97             {
 98                 if(s[x])add(lef[x], -1);
 99                 else add(lef[x], 1);
100                 s[x] = !s[x];///更新该点是否有苹果
101             }
102         }
103     }
104     return 0;
105 }

 

posted @ 2018-04-25 21:34  _努力努力再努力x  阅读(139)  评论(0)  编辑  收藏  举报