POJ-2299 Ultra-QuickSort---树状数组求逆序对+离散化
题目链接:
https://vjudge.net/problem/POJ-2299
题目大意:
本题要求对于给定的无序数组,求出经过最少多少次相邻元素的交换之后,可以使数组从小到大有序。
两个数(a, b)的排列,若满足a > b,则称之为一个逆序对。
n < 500,000 0 ≤ a[i] ≤ 999,999,999
解题思路:
由于数据范围大,可以考虑离散化。
为什么要离散化?
离散化的目的就在于将这么多的数字转化成1-500000以内,然后开一个tree树状数组,下标就对应着数值
如何离散化?
从小到大离散化成1-n,比如数组9 1 0 5 4 离散化成5 2 1 4 3,然后就可以用树状数组做了。
开了树状数组,接下来怎么做?
从左往右依次往树状数组中加入元素,每次加入的时候,在对应下标的位置的数字加一,加入之后数一下在这个下标后面有多少个1,就是加入该数字的逆序对的数目
下面进行模拟 5 2 1 4 3,模拟之后你就懂了
最初的树状数组:
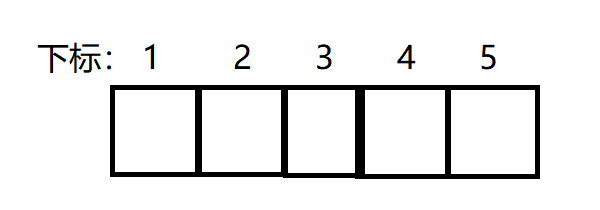
1、首先加入5,此时树状数组的第5个元素+1(红块表示加1),此时5的后面没有元素,所以加入5的逆序对为0,ans = 0
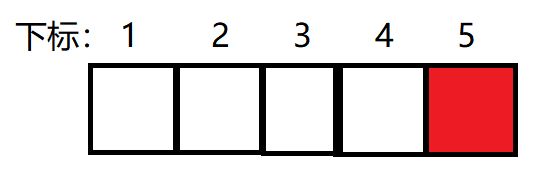
2、加入2,此时第2个元素加1,2的后面有一个红块(表示加一),所以加入2的逆序对为1, ans = 1

3、加入1,此时第1个元素加1,1的后面有两个红块(表示加一),所以加入1的逆序对为2, ans = 3
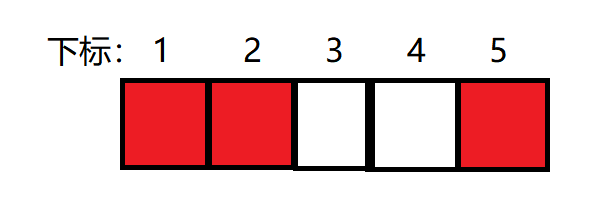
4、加入4,此时第4个元素加1,4的后面有一个红块(表示加一),所以加入4的逆序对为1, ans =4
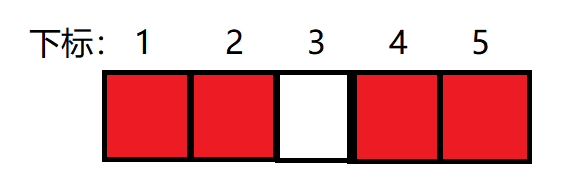
5、加入3,此时第3个元素加1,3的后面有两个红块(表示加一),所以加入3的逆序对为2, ans = 6

利用树状数组可以在o(log(n))的时间复杂度求出当前数字的前缀和,进而可以求出在当前数字后面数字的个数(i-sum(x))(i表示已经加入的总数字的数目,sum(x)表示小于等于x的数字的数目,它们之差就是大于x的数字的数目)
这样就把逆序对问题和树状数组联系起来了。
还有需要注意的地方:
如果,数据之中有数字相等的情况,离散化应该怎么处理呢?
举个例子 2 2 2 2,如果离散化成1 2 3 4,那么每次加入的时候在树状数组中找比它大的元素个数,求出的逆序对为0,正确,这种处理不会产生冲突
如果离散化成4 3 2 1,求出的解时6,答案错误,所以在离散化的时候,权值小的离散之后的值小,权值相同的,下标在前面的离散后的值小。
小技巧:
用结构体存权值和id,排序之后根据id创建新的离散化后的数组
上代码:
1 #include<iostream> 2 #include<algorithm> 3 #include<set> 4 #include<cstring> 5 #include<cstdio> 6 using namespace std; 7 const int maxn = 500000 + 10; 8 typedef long long ll; 9 struct node 10 { 11 int x, id; 12 bool operator < (const node& a)const 13 { 14 return x < a.x || x == a.x && id < a.id; 15 //从小到大排序,如果x相等,那么编号小的排在前面 16 //这是因为这样的话之后离散化的时候,编号小的离散化的数字也是小的 17 //之后求逆序对时需要按照原来ID顺序一个一个放离散化的数字 18 //相同的x最开始放入的值是小的,后面放入的值是大的,这样不会额外增加逆序对 19 //比如一个数组2 2 2 2 按照上述方法离散化成1 2 3 4,逆序对为0。 20 //如果离散化成4 3 2 1,则逆序对就会求错了 21 } 22 }a[maxn]; 23 int b[maxn]; 24 int tree[maxn]; 25 int n; 26 int lowbit(int x) 27 { 28 return x & (-x); 29 } 30 void add(int x, int d) 31 { 32 while(x <= n) 33 { 34 tree[x] += d; 35 x += lowbit(x); 36 } 37 } 38 ll sum(int x) 39 { 40 ll ret = 0; 41 while(x > 0)//此处等于0会导致无限循环 42 { 43 ret += tree[x]; 44 x -= lowbit(x); 45 } 46 return ret; 47 } 48 int main() 49 { 50 while(cin >> n && n) 51 { 52 memset(tree, 0, sizeof(tree)); 53 memset(a, 0, sizeof(a)); 54 memset(b, 0, sizeof(b)); 55 for(int i = 1; i <= n; i++) 56 { 57 scanf("%d", &a[i].x); 58 a[i].id = i; 59 } 60 sort(a + 1, a + n + 1); 61 for(int i = 1; i <= n; i++) 62 { 63 b[a[i].id] = i;//离散化操作,根据原来的id,进行大小的编号,从小到大编号1-n 64 } 65 ll ans = 0; 66 for(int i = 1; i <= n; i++) 67 { 68 add(b[i], 1);//将b[i]加入树状数组中 69 ans += i - sum(b[i]);//i-sum(b[i])表示目前加入了i个数,其中有sum(b[i])个数字比b[i]小,相减的结果就是目前比b[i]大的数字数目 70 } 71 cout<<ans<<endl; 72 } 73 return 0; 74 }
离散化的另一种方式
之前是从小到大离散化,现在从大到小离散化,9 1 0 5 4 离散化成1 4 5 2 3,那进行树状数组求值的时候,每加入一个数,求前面比它小的数字即可,正好是树状数组的sum函数的作用
比如上述例子
1 4 5 2 3
加入1时,没有比1小的,ans=0
加入4时,有1个比4小,ans = 1;
加入5是,有2个比5小,ans = 3;
。。。。。。
同理,上述的有重复元素的时候2 2 2 2离散化成1 2 3 4的时候是错误的,因为这里是找比该数小的数字,所以1 2 3 4求出逆序对为6,是错误的
离散化成4 3 2 1的话,就是正确的。
上代码:(找不同,好好看看就懂了)
1 #include<iostream> 2 #include<algorithm> 3 #include<set> 4 #include<cstring> 5 #include<cstdio> 6 using namespace std; 7 const int maxn = 100000 + 10; 8 typedef long long ll; 9 struct node 10 { 11 int x, id; 12 bool operator < (const node& a)const 13 { 14 return x > a.x || x == a.x && id > a.id;//这里变啦!!! 15 } 16 }a[maxn]; 17 int b[maxn]; 18 int tree[maxn]; 19 int n; 20 int lowbit(int x) 21 { 22 return x & (-x); 23 } 24 void add(int x, int d) 25 { 26 while(x <= n) 27 { 28 tree[x] += d; 29 x += lowbit(x); 30 } 31 } 32 ll sum(int x) 33 { 34 ll ret = 0; 35 while(x > 0)//此处等于0会导致无限循环 36 { 37 ret += tree[x]; 38 x -= lowbit(x); 39 } 40 return ret; 41 } 42 int main() 43 { 44 while(cin >> n) 45 { 46 memset(tree, 0, sizeof(tree)); 47 memset(a, 0, sizeof(a)); 48 memset(b, 0, sizeof(b)); 49 for(int i = 1; i <= n; i++) 50 { 51 scanf("%d", &a[i].x); 52 a[i].id = i; 53 } 54 sort(a + 1, a + n + 1); 55 for(int i = 1; i <= n; i++) 56 { 57 b[a[i].id] = i;//离散化操作,根据原来的id,进行大小的编号,从大到小编号1-n 58 } 59 ll ans = 0; 60 for(int i = 1; i <= n; i++)//还有下面的两行 61 { 62 ans += sum(b[i]);//下标比b[i]小,但是实际的数字比b[i]大(因为离散化的时候就是数字大的编号小) 63 add(b[i], 1);//要先调用sum,再调用add,因为先调用add的话,求sum的时候把自己也算进去了 64 } 65 cout<<ans<<endl; 66 } 67 }



